Лицей №146 из 6 в 7 класс 2023 вариант 2

1. Вычислите: \[ \bigl(1{,}05 \;\cdot\;(0{,}15 - 1)\bigr)\;\cdot\;2\tfrac14 + 1{,}25. \]
2. Найдите наибольшее трёхзначное число, которое делится на 2 и на 9.
3. Из двух одинаковых квадратов сложили прямоугольник. Найдите площадь данного квадрата, если периметр прямоугольника равен 48 см.
4. Тетрадь стоит 40 рублей. Сколько тетрадей можно будет купить на 250 рублей после повышения цены на $10\%$?
5. Решите уравнение: \[ 4\Bigl(x - \tfrac23\Bigr) + 3\Bigl(x + 1\tfrac23\Bigr) = -9{,}5. \]
6. В двух вазах было 400 орехов. После того, как из первой вазы съели 121 орех, а из второй – 143 ореха, в вазах осталось орехов поровну. Сколько орехов было во второй вазе?
7. Найдите площадь фигуры, изображённой на рисунке:
   
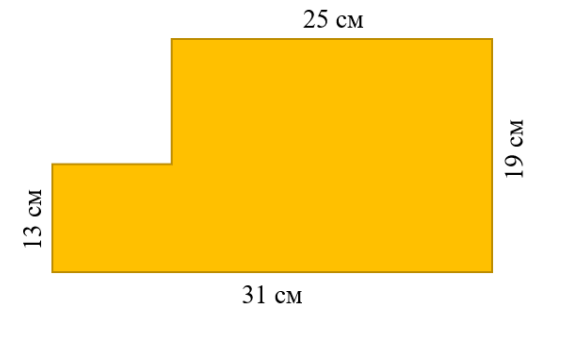
   (Ширины указаны: 21 см, 28 см, 19 см; высоты: 9 см, 12 см.)

1. У Василисы Прекрасной 5 дочерей, которые рождались ровно через 3 года друг за другом. Сейчас им вместе 60 лет. Сколько лет младшей?
2. Сколько существует таких натуральных чисел \(M\), для которых ровно одно из чисел \(M\) и \(M+641\) является трёхзначным?
3. Найдите сумму цифр числа \(10^{28} - 10^{9}\).
4. У какого числа от 2381895 до 2761984 самая маленькая сумма цифр?
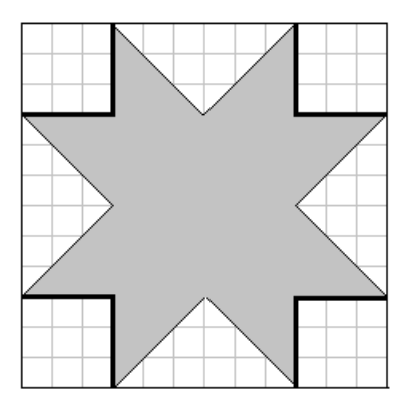
5. В углах квадрата \(12\times12\) вырезали маленькие квадратики \(3\times3\). Найдите площадь закрашенной области (см. рисунок).
   
   
6. Сколько существует трёхзначных чисел, произведение цифр которых равно 30?
7. В 2023 году в школе трижды проводились турниры по шахматам. В каждом соревновании принимали участие по 40 учащихся. При этом 70 учащихся только один раз участвовали, а 10 учащихся – ровно по 2 раза. Сколько учащихся принимали участие во всех трёх турнирах?
8. За 2 023 удара волшебной палочки Фея может сам осекол расколдовать свою чашку. Один взмах ослабляет её на 1 % крепости. Сколько взмахов потребуется, чтобы вернуть чашку полностью?
9. Однаковую степень двойки наибольшим образом делит число \(10^{146} - 10^7\)? Укажите показатель этой степени.
10. В июне прошлого года количество солнечных дней в Перми составляло 25% от пасмурных, а количество тёплых дней – 20% от прохладных. Только 3 дня были тёплыми и солнечными. Сколько дней были пасмурными и прохладными?

Решения задач

1. Вычислите: \[ \bigl(1{,}05 \cdot (0{,}15 - 1)\bigr) \cdot 2\tfrac{1}{4} + 1{,}25 \] Решение: \[ (0{,}15 - 1) = -0{,}85 \] \[ 1{,}05 \cdot (-0{,}85) = -0{,}8925 \] \[ 2\tfrac{1}{4} = 2{,}25 \quad \Rightarrow \quad -0{,}8925 \cdot 2{,}25 = -2{,}008125 \] \[ -2{,}008125 + 1{,}25 = -0{,}758125 \] Ответ: \(-0{,}758125\).
   
   
2. Найдите наибольшее трёхзначное число, которое делится на 2 и на 9. Решение: Число должно оканчиваться на чётную цифру и иметь сумму цифр, кратной 9. Наибольшее трёхзначное число 999 → 998 (26 → нет) → 996 (24 → нет) → 990 (18 → да). Ответ: 990.
   
   
3. Из двух одинаковых квадратов сложили прямоугольник. Найдите площадь квадрата, если периметр прямоугольника равен 48 см. Решение: Пусть сторона квадрата \(a\), тогда стороны прямоугольника \(a\) и \(2a\). Периметр: \[ 2(a + 2a) = 6a = 48 \quad \Rightarrow \quad a = 8 \text{ см} \] Площадь квадрата: \[ a^2 = 8^2 = 64 \text{ см}^2 \] Ответ: 64 см².
   
   
4. Тетрадь стоит 40 руб. Сколько тетрадей можно купить на 250 руб после повышения цены на $10\%$. Решение: Новая цена: \[ 40 \cdot 1{,}1 = 44 \text{ руб.} \] \[ \left\lfloor \frac{250}{44} \right\rfloor = 5 \] Ответ: 5.
   
   
5. Решите уравнение: \[ 4\left(x - \tfrac{2}{3}\right) + 3\left(x + 1\tfrac{2}{3}\right) = -9{,}5 \] Решение: \[ 4x - \tfrac{8}{3} + 3x + 5 = -9{,}5 \] \[ 7x + \tfrac{7}{3} = -\tfrac{19}{2} \] \[ x = -\tfrac{71}{42} \] Ответ: \(-\tfrac{71}{42}\).
   
   
6. В двух вазах было 400 орехов. После того, как из первой съели 121 орех, а из второй — 143, осталось поровну. Сколько орехов было во второй вазе? Решение: Пусть во второй вазе \(y\) орехов: \[ x + y = 400 \] \[ x - 121 = y - 143 \quad \Rightarrow \quad x - y = -22 \] \[ x = 189, \quad y = 211 \] Ответ: 211.
   
   
7. Найдите площадь фигуры. Решение: Составная фигура из прямоугольников: \[ 21 \cdot 9 + 28 \cdot 12 = 189 + 336 = 525 \text{ см}^2 \] Ответ: 525 см².
   
   
8. У Василисы 5 дочерей с разницей в 3 года. Им вместе 60 лет. Сколько лет младшей? Решение: Пусть младшей \(x\) лет: \[ x + (x + 3) + (x + 6) + (x + 9) + (x + 12) = 60 \] \[ 5x + 30 = 60 \quad \Rightarrow \quad x = 6 \] Ответ: 6.
   
   
9. Сколько чисел \(M\), для которых ровно одно из чисел \(M\) или \(M+641\) трёхзначно? Решение: \(M\) трёхзначно, \(M+641\) — нет: \(359 \leq M \leq 999\) (641 число). \(M\) не трёхзначно, \(M+641\) — трёхзначно: \(1 \leq M \leq 358\) (не трёхзначны 1-99). Всего: \(641 + 99 = 740\). Ответ: 740.
   
   
10. Сумма цифр числа \(10^{28} - 10^9\). Решение: \(10^{28} - 10^9 = 999\ldots999000\ldots000\) (19 девяток, 9 нулей). Сумма цифр: \[ 19 \cdot 9 = 171 \] Ответ: 171.
    
    
11. Число с минимальной суммой цифр между 2381895 и 2761984. Ответ: 2400000 (сумма цифр 2+4=6).
    
    
12. Площадь после вырезания углов 3×3 из квадрата 12×12. Решение: \[ 12 \cdot 12 - 4 \cdot (3 \cdot 3) = 144 - 36 = 108 \] Ответ: 108.
    
    
13. Трёхзначные числа с произведением цифр 30. Ответ: Перестановки \(1,5,6\) и \(2,3,5\) → \(6 + 6 = 12\) чисел.
    
    
14. Участники трёх турниров. Решение: Пусть \(c\) — участвовали во всех трёх: \[ 70 \cdot 1 + 10 \cdot 2 + c \cdot 3 = 120 \quad \Rightarrow \quad c = 10 \] Ответ: 10.
    
    
15. Взмахов для расколдовывания чашки. Ответ: 100 взмахов (каждый снижает на 1\%).
    
    
16. Наибольшая степень двойки в \(10^{146} -10^7\). Ответ: \(10^7(10^{139} -1) \Rightarrow\) степень двойки 7.
    
    
17. Пасмурные и прохладные дни в Перми. Решение: \(T = 5\), \(C = 25\), S = пасмурные и прохладные: \[ PC = C - (S - 3) = 25 - 3 = 22 \] Ответ: 22.