Лицей №146 из 6 в 7 класс 2022 вариант 2

1. Выполните действия: \[ 25\tfrac{2}{3} - \tfrac{3}{11} + 12\tfrac{3}{5} : 2{,}1. \]
2. Найдите наибольший общий делитель чисел $378$ и $396$.
3. Вычислите: \[ -5{,}34 - \bigl|-2{,}72\bigr| + 4{,}34 + 6{,}72. \]
4. Найдите наименьшее трёхзначное число $x$, при котором выражение \[ (x - 52) \] делится на $5$.
5. У Васи с Машей было поровну денег. Когда Вася купил книгу за 700 р., а Маша — журнал за 300 р., у Маши осталось денег в 3 раза больше, чем у Васи. Сколько рублей было у каждого из них вначале?
6. Сколько существует натуральных чисел $m$, больших $65\%$ числа 44, но меньших $\tfrac{4}{3}$ числа 31?
7. Один рабочий может выполнить заказ за 6 часов, а другой — за 8 часов. Какую часть заказа останется выполнить после 3 часов их совместной работы? Ответ запишите в виде десятичной дроби.
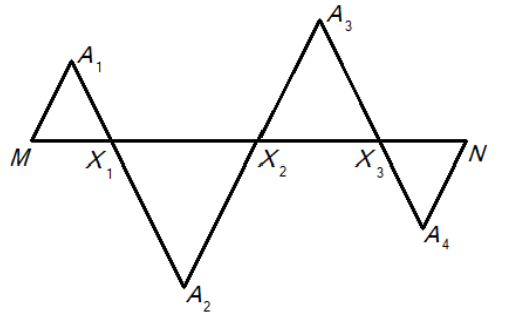
8. Отрезок $MN$ длиной 17 разбит точками $X_1,X_2,X_3$ на четыре неравных отрезка. На этих отрезках построены равносторонние треугольники $MA_1X_1$, $X_1A_2X_2$, $X_2A_3X_3$, $X_3A_4N$ (см. рис.). Найдите длину ломаной $MA_1X_1A_2X_2A_3X_3A_4N$.
   
   Задачи, оцениваемые в 2 балла
9. Саша задумал число, умножил его на 20, из результата вычел 900, полученное число разделил на 101, к результату прибавил 5 и, наконец, умножил на 4, получил 100. Какое число задумал Саша?
10. Отрезок делит прямоугольник на квадрат и прямоугольник, причём площадь квадрата в 3 раза больше площади прямоугольника. Во сколько раз периметр квадрата больше периметра прямоугольника?
11. Мальчик в парке кидает дротики в воздушные шарики. Он заплатил за 10 дротиков. За каждое попадание ему давали ещё 2 дротика. Всего он сделал 16 бросков. Сколько раз он попал в цель?
12. Саша написал число 531, после чего Юля приписала одну цифру слева и одну цифру справа так, что получившееся число делится на 72. Какое число получилось у Юли?
13. Сколько трёхзначных чисел имеет в своей записи ровно 2 одинаковые цифры?
14. В трёх электричках разное число мест: 265, 318 и 477. Во всех вагонах число мест одинаковое и больше 30. Сколько всего вагонов в этих поездах вместе?
15. По кругу стоят 32 ребёнка. Дед Мороз дарит им подарки: первому — 4, второму — 2, следующему — 4, потом — 2 и так далее. Всего он подарил 112 подарков. Сколько детей получили ровно 4 подарка?
16. На конкурсе мастеров каждая поделка оценивалась в целое число баллов от 1 до 20, но в окончательный подсчёт участнику засчитываются только 4 лучших поделки. За 5 поделок Петя набрал 82 балла. Какой наименьший результат может получиться при окончательном подсчёте?

Решения задач

1. Выполните действия: \[ 25\tfrac{2}{3} - \tfrac{3}{11} + 12\tfrac{3}{5} : 2{,}1. \] Решение: \( 25\tfrac{2}{3} = \frac{77}{3}, \quad 12\tfrac{3}{5} = \frac{63}{5}, \quad 2{,}1 = \frac{21}{10}. \) Выполним деление: \[ \frac{63}{5} : \frac{21}{10} = \frac{63}{5} \cdot \frac{10}{21} = 6. \] Теперь вычитаем и складываем: \[ \frac{77}{3} - \frac{3}{11} + 6 = \frac{77 \cdot 11 - 3 \cdot 3}{33} + 6 = \frac{847}{33} + 6 = \frac{847 + 198}{33} = \frac{1045}{33} = 31\frac{22}{33}. \] Ответ: \( 31\frac{22}{33} \).
   
   
2. Найдите наибольший общий делитель чисел 378 и 396.
   Решение: Разложим числа на простые множители: \[ 378 = 2 \cdot 3^3 \cdot 7, \quad 396 = 2^2 \cdot 3^2 \cdot 11. \] Общие простые множители с минимальными степенями: \( 2^1 \cdot 3^2 = 18 \).
   Ответ: 18.
   
   
3. Вычислите: \[ -5{,}34 - \bigl|-2{,}72\bigr| + 4{,}34 + 6{,}72. \] Решение: \[ -5{,}34 - 2{,}72 + 4{,}34 + 6{,}72 = (-5{,}34 + 4{,}34) + (-2{,}72 + 6{,}72) = -1 + 4 = 3. \] Ответ: 3.
   
   
4. Найдите наименьшее трёхзначное число \( x \), при котором выражение \( x - 52 \) делится на 5.
   Решение: \( x - 52 \equiv 0 \pmod{5} \Rightarrow x \equiv 52 \pmod{5} \Rightarrow x \equiv 2 \pmod{5} \). Наименьшее трёхзначное: 102 (проверка: \( 102 - 52 = 50 \), делится на 5).
   Ответ: 102.
   
   
5. У Васи с Машей было поровну денег. После покупок у Васи осталось \( S - 700 \), у Маши \( S - 300 \). По условию: \[ S - 300 = 3(S - 700) \Rightarrow S - 300 = 3S - 2100 \Rightarrow 2S = 1800 \Rightarrow S = 900. \] Ответ: 900 рублей.
   
   
6. Число \( m \) должно удовлетворять: \[ 0{,}65 \cdot 44 = 28{,}6 < m < \tfrac{4}{3} \cdot 31 \approx 41{,}33. \] Натуральные \( m \): 29, 30, ..., 41. Всего 13 чисел.
   Ответ: 13.
   
   
7. Совместная производительность: \[ \frac{1}{6} + \frac{1}{8} = \frac{7}{24} \text{ за час.} \] За 3 часа выполнили: \[ 3 \cdot \frac{7}{24} = \frac{7}{8} \Rightarrow \text{Осталось } \frac{1}{8} = 0{,}125. \] Ответ: 0,125.
   
   
8. Каждый отрезок \( MX_1, X_1X_2, X_2X_3, X_3N \) равен стороне соответствующего равностороннего треугольника. Ломаная содержит по две стороны каждого треугольника: \[ 2(MX_1 + X_1X_2 + X_2X_3 + X_3N) = 2 \cdot 17 = 34. \] Ответ: 34.
   
   
9. Решим уравнение: \[ \left(\frac{20x - 900}{101} + 5\right) \cdot 4 = 100 \Rightarrow \frac{20x - 900}{101} = 20 \Rightarrow 20x = 2920 \Rightarrow x = 146. \] Ответ: 146.
   
   
10. Пусть площадь квадрата \( a^2 \), прямоугольника \( \frac{a^2}{3} \Rightarrow a = 3b \). Периметр квадрата \( 4a = 12b \), прямоугольника \( 2(a + b) = 8b \). Отношение: \( \frac{12b}{8b} = 1{,}5 \).
    Ответ: 1,5.
    
    
11. Всего бросков: 10 (начальные) + 2x (за попадания) = 16 $\Rightarrow$ 2x = 6 $\Rightarrow$ x = 3.
    Ответ: 3.
    
    
12. Искомое число делится на 8 и 9. Проверим делимость на 8 для \( \overline{31B} \). Вариант: \( B = 2 \) (312). Сумма цифр \( A + 5 + 3 + 1 + 2 = A + 11 \). При \( A = 7 \): 18 (делится на 9). Число: 75312.
    Ответ: 75312.
    
    
13. Трёхзначные числа с ровно двумя одинаковыми цифрами: \[ 3 \times (9 \times 9) = 243 \text{ (3 позиции для пары)}. \] Ответ: 243.
    
    
14. Найдём НОД чисел: 265, 318, 477. НОД(265, 318) = 53; проверяем 53 с 477: 477 ÷ 53 = 9. Общий делитель 53. Количество вагонов: \[ \frac{265}{53} + \frac{318}{53} + \frac{477}{53} = 5 + 6 + 9 = 20. \] Ответ: 20.
    
    
15. Каждый полный круг содержит 16 «четвёрок» и 16 «двоек». За 3 круга и 8 дополнительных подарков: первые 16 детей получили 4 подарка.
    Ответ: 16.
    
    
16. Пример: оценки 20, 20, 14, 14, 14. Сумма: 82. Минимальный из четырёх лучших: 14.
    Ответ: 14.