Лицей №146 из 6 в 7 класс 2019 год вариант 4

1. Вычислите \[ \biggl(\frac{1\cdot2\cdot3 + 2\cdot4\cdot6 + 3\cdot6\cdot9 + \dots + 15\cdot30\cdot45} {1\cdot3\cdot5 + 2\cdot6\cdot10 + 3\cdot9\cdot15 + \dots + 15\cdot45\cdot75} \biggr)^{2}. \]
   
   
2. В числе \(A\) запятую перенесли влево на один знак и получили число \(B\), а затем ещё раз влево на один знак и получили число \(C\). Найдите число \(A\), если \[ A - B + C = 19{,}11. \]
   
   
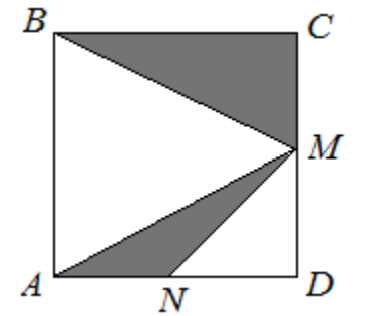
3. Площадь квадрата \(ABCD\) равна \(16\) м\(^2\). Точки \(M\) и \(N\) — середины его сторон. Определите площадь закрашенной части (см. рис.).
   
   
   
   
4. Найдите все целые \(n\), при которых дробь \[ \frac{7n^2 + 3n - 10}{n} \] принимает натуральные значения.

Решения задач

1. Вычислите $\left( \frac{1\cdot2\cdot3 + 2\cdot4\cdot6 + 3\cdot6\cdot9 + \dots + 15\cdot30\cdot45}{1\cdot3\cdot5 + 2\cdot6\cdot10 + 3\cdot9\cdot15 + \dots + 15\cdot45\cdot75} \right)^{2}$.
   Решение: Числитель каждого слагаемого в числителе соответствует $k \cdot (2k) \cdot (3k) = 6k^3$, а в знаменателе $k \cdot (3k) \cdot (5k) = 15k^3$. Тогда: \[ \frac{6(1^3 + 2^3 + \dots + 15^3)}{15(1^3 + 2^3 + \dots + 15^3)} = \frac{6}{15} = \frac{2}{5} \] Возводим в квадрат: \[ \left( \frac{2}{5} \right)^2 = \frac{4}{25} \] Ответ: $\left( \frac{4}{25} \right)$.
   
   
2. В числе $A$ запятую перенесли влево на один знак и получили число $B$, а затем ещё раз влево на один знак и получили число $C$. Найдите число $A$, если $A - B + C = 19{,}11$.
   Решение: \[ B = \frac{A}{10}, \quad C = \frac{B}{10} = \frac{A}{100} \] Подставляем в уравнение: \[ A - \frac{A}{10} + \frac{A}{100} = 19{,}11 \implies \frac{91A}{100} = 19{,}11 \implies A = \frac{1911}{91} = 21 \] Ответ: $21$.
   
   
3. Площадь квадрата $ABCD$ равна $16$ м$^2$. Точки $M$ и $N$ — середины его сторон. Определите площадь закрашенной части.
   Решение: Сторона квадрата $4$ м. Закрашенная фигура — квадрат, образованный соединением середин сторон. Каждая сторона внутреннего квадрата равна диагонали прямоугольного треугольника с катетами $2$ м. Длина диагонали $2\sqrt{2}$ м. Площадь внутреннего квадрата: \[ (2\sqrt{2})^2 = 8 \text{ м}^2 \] Ответ: $8$ м$^2$.
   
   
4. Найдите все целые $n$, при которых дробь $\frac{7n^2 + 3n - 10}{n}$ принимает натуральные значения.
   Решение: \[ \frac{7n^2 + 3n - 10}{n} = 7n + 3 - \frac{10}{n} \] Чтобы выражение было целым, $\frac{10}{n}$ должно быть целым. Возможные делители $10$: $\pm1, \pm2, \pm5, \pm10$. \[ \begin{aligned} n = -1: & \quad 7(-1) + 3 - \frac{10}{-1} = -7 +3 +10 =6 \quad (\text{натуральное}) \\ n = 2: & \quad 7(2) +3 - \frac{10}{2} =14 +3 -5 =12 \quad (\text{натуральное}) \\ n = 5: & \quad 7(5) +3 - \frac{10}{5}=35 +3 -2 =36 \quad (\text{натуральное}) \\ n = 10: & \quad 7(10)+3 - \frac{10}{10}=70 +3 -1 =72 \quad (\text{натуральное}) \\ \end{aligned} \] Ответ: $-1, 2, 5, 10$.