Лицей №146 из 6 в 7 класс 2019 год вариант 3

1. Вычислите \[ \biggl(\frac{1\cdot2\cdot4 + 2\cdot4\cdot8 + 3\cdot6\cdot12 + \dots + 10\cdot20\cdot40} {1\cdot4\cdot5 + 2\cdot8\cdot10 + 3\cdot12\cdot15 + \dots + 10\cdot40\cdot50} \biggr)^{2}. \]
   
   
2. В числе \(A\) запятую перенесли вправо на один знак и получили число \(B\), а затем ещё на один знак вправо и получили число \(C\). Найдите число \(A\), если \[ C + B - A = 13{,}08. \]
   
   
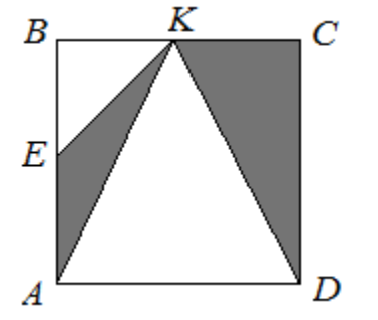
3. Площадь квадрата \(ABCD\) равна \(8\) м\(^2\). Точки \(E\) и \(K\) — середины его сторон. Определите площадь закрашенной части (см. рис.).
   
   
   
   
4. Найдите все целые \(n\), при которых дробь \[ \frac{9n^2 + 3n - 14}{n} \] принимает натуральные значения.

Решения задач

1. Вычислите \[ \biggl(\frac{1\cdot2\cdot4 + 2\cdot4\cdot8 + 3\cdot6\cdot12 + \dots + 10\cdot20\cdot40} {1\cdot4\cdot5 + 2\cdot8\cdot10 + 3\cdot12\cdot15 + \dots + 10\cdot40\cdot50} \biggr)^{2}. \]
   Решение:
   Рассмотрим общий член числителя:
   $k \cdot 2k \cdot 4k = 8k^3$ (для $k$ от 1 до 10).
   Сумма числителя: $8(1^3 + 2^3 + \dots + 10^3)$.
   Общий член знаменателя:
   $k \cdot 4k \cdot 5k = 20k^3$.
   Сумма знаменателя: $20(1^3 + 2^3 + \dots + 10^3)$.
   Отношение равно $\frac{8}{20} = \frac{2}{5}$.
   Квадрат отношения: $\left(\frac{2}{5}\right)^2 = \frac{4}{25}$.
   Ответ: $\frac{4}{25}$.
2. В числе \(A\) запятую перенесли вправо на один знак и получили число \(B\), а затем ещё на один знак вправо и получили число \(C\). Найдите число \(A\), если \[ C + B - A = 13{,}08. \]
   Решение:
   По условию:
   $B = 10A$, $C = 100A$.
   Уравнение: $100A + 10A - A = 13{,}08$.
   $109A = 13{,}08 \implies A = \frac{13{,}08}{109} = 0{,}12$.
   Проверка: $C = 12$, $B = 1{,}2$, $12 + 1{,}2 - 0{,}12 = 13{,}08$.
   Ответ: $0{,}12$.
3. Площадь квадрата \(ABCD\) равна \(8\) м\(^2\). Точки \(E\) и \(K\) — середины его сторон. Определите площадь закрашенной части.
   Решение:
   Сторона квадрата: $\sqrt{8} = 2\sqrt{2}$ м. Точки делят стороны пополам. Закрашенная фигура — восьмиугольник, образованный удалением четырёх треугольников из углов квадрата.
   Каждый треугольник имеет катеты $\sqrt{2}$ м. Площадь одного треугольника: $\frac{1}{2} \cdot \sqrt{2} \cdot \sqrt{2} = 1$ м².
   Всего удалено $4 \cdot 1 = 4$ м². Закрашенная площадь: $8 - 4 = 4$ м².
   Ответ: $4$ м².
4. Найдите все целые \(n\), при которых дробь \[ \frac{9n^2 + 3n - 14}{n} \] принимает натуральные значения.
   Решение:
   Упростим дробь: $9n + 3 - \frac{14}{n}$.
   Для натуральности дроби $n$ должно быть целым делителем $14$: $n \in \{\pm1, \pm2, \pm7, \pm14\}$.
   Проверяем:
   - $n = -1$: $\frac{9(-1)^2 + 3(-1) - 14}{-1} = \frac{9 - 3 - 14}{-1} = 8$ ✓
   - $n = 2$: $\frac{36 + 6 - 14}{2} = \frac{28}{2} = 14$ ✓
   - $n = 7$: $\frac{441 + 21 - 14}{7} = \frac{448}{7} = 64$ ✓
   - $n = 14$: $\frac{1764 + 42 - 14}{14} = \frac{1792}{14} = 128$ ✓
   Остальные значения дают нецелые или отрицательные результаты.
   Ответ: $n \in \{-1, 2, 7, 14\}$.