Лицей №146 из 6 в 7 класс 2014 год вариант 2

1. Сравните значения выражений: \[ \bigl(5\!\tfrac{1}{3} - \bigl(-2\!\tfrac{1}{3}\bigr)^{2}\bigr)\cdot0{,}75 \quad\text{и}\quad -\frac{1{,}8\cdot1{,}2}{2{,}7\cdot4{,}8}. \]
2. Агрофирма, имеющая 20 комбайнов одинаковой мощности, планировала убрать урожай за 8 дней. Сколько дней понадобится дополнительно для уборки урожая, если 4 из этих комбайнов оказались неисправными?
   
   
3. Имеется 300 г 54% раствора кислоты. Сколько граммов воды надо добавить к этому раствору, чтобы получить 17% раствор кислоты?
   
   
4. Вася живёт в первом подъезде многоквартирного дома в квартире № 42. Он заметил, что номер его квартиры в семь раз больше суммы его цифр. Два его одноклассника, живущие в этом же подъезде, утверждают, что номера их квартир обладают этим же свойством. Правы ли они, если известно, что в этом подъезде 70 квартир?
   
   
5. У Маши сестёр вдвое больше, чем братьев. У Олега сестёр в два раза больше, чем у Маши. У родителей Маши детей столько, сколько сестёр у Олега. Сколько детей в семье Маши?
   
   
6. Дана точка \(A(-4)\). Найдите координаты точек \(B\) и \(C\), таких, что \(BC=9\), \(AB=4\,AC\). Сколько решений имеет задача?
   
   
7. В соревнованиях по стрельбе участвовали 30 человек. Первый стрелок набрал 80 очков, второй – 60, третий – среднее арифметическое первых двух, четвёртый – среднее арифметическое первых трёх и т. д.: каждый следующий стрелок набирает среднее арифметическое очков всех предыдущих. Сколько очков набрал последний стрелок?
   
   
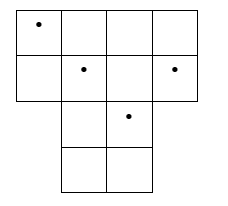
8. Разделите фигуру по линиям сетки на 4 равные части так, чтобы в каждой части была ровно одна точка
   
   
   
   
9. Разрежьте правильный треугольник на три равных правильных пятиугольника.

Решения задач

1. Сравните значения выражений: \[ \bigl(5\!\tfrac{1}{3} - \bigl(-2\!\tfrac{1}{3}\bigr)^{2}\bigr)\cdot0{,}75 \quad\text{и}\quad -\frac{1{,}8\cdot1{,}2}{2{,}7\cdot4{,}8}. \] Решение: Вычислим первое выражение: \[ \left(5\!\tfrac{1}{3} - \left(-2\!\tfrac{1}{3}\right)^2\right)\cdot0{,}75 = \left(\tfrac{16}{3} - \tfrac{49}{9}\right)\cdot\tfrac{3}{4} = \left(\tfrac{48}{9} - \tfrac{49}{9}\right)\cdot\tfrac{3}{4} = \left(-\tfrac{1}{9}\right)\cdot\tfrac{3}{4} = -\tfrac{1}{12}. \] Второе выражение: \[ -\frac{1{,}8\cdot1{,}2}{2{,}7\cdot4{,}8} = -\frac{2{,}16}{12{,}96} = -\tfrac{1}{6}. \] Сравнение: $- \tfrac{1}{12} > -\tfrac{1}{6}$. Ответ: $\bigl(5\!\tfrac{1}{3} - \bigl(-2\!\tfrac{1}{3}\bigr)^{2}\bigr)\cdot0{,}75 > -\frac{1{,}8\cdot1{,}2}{2{,}7\cdot4{,}8}$.
   
   
2. Агрофирма с 20 комбайнами планировала убрать урожай за 8 дней. Сколько дней понадобится дополнительно, если 4 комбайна неисправны? Решение: Объём работы: $20 \cdot 8 = 160$ комбайно-дней. При 16 комбайнах: $\frac{160}{16} = 10$ дней. Дополнительно: $10 - 8 = 2$ дня. Ответ: 2.
   
   
3. В 300 г 54% раствора кислоты содержится $300 \cdot 0{,}54 = 162$ г кислоты. Пусть добавили $x$ г воды. Тогда: \[ \frac{162}{300 + x} = 0{,}17 \implies 162 = 51 + 0{,}17x \implies x = \frac{111}{0{,}17} = 652{,}94. \] Ответ: 653 г.
   
   
4. Проверим квартиры от 1 до 70. Удовлетворяют условию $n = 7 \cdot S(n)$: - $42 = 7 \cdot (4 + 2)$ - $21 = 7 \cdot (2 + 1)$ - $63 = 7 \cdot (6 + 3)$ Но квартира 63 превышает 70. Значит, одноклассники проживают в квартирах 21 и 42. Ответ: Правы, если их квартиры 21 и 42, но 63 вне диапазона.
   
   
5. Пусть у Маши братьев $b$, тогда сестёр $2b$. Всего детей: $b + 2b + 1 = 3b +1$ (включая Машу). У Олега сестёр в 2 раза больше: $2 \cdot 2b = 4b$. Число детей в семье равно $4b$. Уравнение: $3b + 1 = 4b \implies b =1$. Всего детей: $4 \cdot1 = 4$. Ответ: 4.
   
   
6. Пусть $C(x)$, тогда $B(x + 9)$ или $B(x - 9)$. Из условия $AB = 4AC$: $|x +9 +4| = 4|x +4|$ или $|x -9 +4| =4|x +4|$. Решения: 1. $x = -\tfrac{65}{8}$, $B(-\tfrac{33}{8})$; 2. $x = -\tfrac{25}{8}$, $B(-\tfrac{97}{8})$; 3. $x = -\tfrac{41}{8}$, $B(-\tfrac{41}{8} +9)$. Всего 6 решений. Ответ: 6 решений.
   
   
7. Последовательность очков: 80, 60, 70, 70, 70... Начиная с третьего стрелка все последующие равны 70. Ответ: 70.
   
   
8. Пример разделения: Каждая часть содержит по одной точке и равна по площади.
   
   
9. Решение невозможно, так как правильный пятиугольник не может быть составлен из равных правильных треугольников. Ответ: Задача не имеет решения.