Лицей №1329 из 4 в 5 класс 2023 год вариант 1

Школа № 1329

2023

Вычисления

1. При решении примеров Егорка перепутал сложение и умножение и забыл указать скобки (но при вычислениях их учитывал!). Ниже записаны ответы Егорки. Восстановите скобки и решите примеры правильно:
   • \(78 + 102 - 75 \cdot 12 = 2118\)
   • \(111 + 22 - 3 \cdot 55 - 15 = 2479\)
   
   
   
2. Вычислите:
   • \((287\,129 - 229\,856) + (872\,109 - 734\,075)\)
   • \(76\,563\,001 - (123\,789 + 803\,005) - (890\,444 - 283\,917)\)
   • \(90\,000 - 205 \cdot 409 - 156\,738 : 519 + 247\)
   • \(849 \cdot (32\,207 : 301 + 74\,160 : 4120) \cdot 4\)
   • \((701 \cdot 352 - 6148 : 58) : 2 - 323\)
   • \(167 \cdot (5047 : 49 + 8232 : 56) \cdot 4\)
   • \((205 \cdot 104 - 74\,601 : 243) \cdot 5 + 5005\)
   • \(183 \cdot (1677 : 43 - 888 : 12 : 2) \cdot 50\)
   
   
   
3. Сравните без вычислений:
   • \(764\,479 + 805\,691\) и \(705\,499 + 864\,671\)
   • \(567 \cdot 9800\) и \(5760 \cdot 980\)
   • \(678\,678\,678 : 678\) и \(678\,678\,678 : 113\)
   • \(789\,453\,204 - 267\,892\,542\) и \(767\,453\,544 - 289\,892\,202\)
   
   
   
4. Какие цифры можно поставить вместо звездочки в каждом из случаев, чтобы получилось верное неравенство:
   
   
   
   
5. Решите уравнение: \[ (3891 - x \cdot 2) + 25419 = 27090 \] \[ 100001 - (150 \cdot x + 44864) = 31587 \]

Текстовые задачи

1. Егор выехал на автомобиле из деревни в город в 7 утра. Через 50 минут он остановился на дозаправку, которая длилась 7 минут. Затем, проехав еще 45 минут, он на 20 минут остановился осмотреть развалины замка. Еще через полчаса он остановился на 5 минут нарвать цветов для мамы. В котором часу Егор приехал в город, если после последней остановки он ехал до города еще 33 минуты?
   
   
2. Петя покупал пирожные. Оказалось, что на 4 пирожных ему не хватило 100 руб, а когда ему мама дала еще 250 руб, он смог на все деньги купить 5 пирожных. Сколько стоит одно пирожное?
   
   
3. Блокнот в обложке стоит 20 рублей. При этом блокнот на 18 рублей дороже обложки. Сколько стоит обложка?
   
   
4. На экскурсию поехало 220 учеников в сопровождении учителей. 6 групп с одинаковым числом школьников отправились на экскурсию в Кремль, а 70 школьников — в Третьяковскую галерею. Сколько денег должна уплатить каждая из 6 групп, если один билет для взрослых стоит 400 рублей, а детский — 200 рублей и в каждой группе двое взрослых?
   
   
5. Цена 8 нотных тетрадей такая же, как и у 9 блокнотов. Какова стоимость одного блокнота, если за 2 нотные тетради нужно заплатить 360 руб.?
   
   
6. Три арбуза и две дыни на 40 руб дешевле, чем три дыни и два арбуза. Сколько стоит 5 арбузов, если две дыни и два арбуза стоят 420 руб?
   
   
7. Кузнецы изготовили 1090 молотков: слесарных, столярных и сапожных. Слесарных и сапожных было 588, столярных и сапожных — 766. Сколько молотков каждого вида было изготовлено?
   
   
8. Пять учеников купили 100 тетрадей. Коля и Вася купили 52 тетради, Вася и Юра — 43 тетради, Юра и Саша — 34 тетради, Саша и Сережа — 30. Сколько тетрадей купил каждый из них?

Задачи на движение

1. Илья Муромец и Алеша Попович скачут навстречу друг другу с разных застав, расстояние между которыми 78 км. Илья Муромец скачет со скоростью 12 км/ч, Алеша Попович — со скоростью 14 км/ч. Какое расстояние проедет до встречи каждый из них, если они выехали одновременно?
   
   
2. Маленький Мук должен был доставить письмо визирю, преодолев 3600 км за 9 часов. Однако на выходе из двора он был на 40 минут задержан. На сколько км/ч ему нужно увеличить скорость, чтобы доставить письмо вовремя?
   
   
3. Из поселка в город, расстояние между которыми 48 км, одновременно вышел пешеход со скоростью 4 км/ч и выехал велосипедист со скоростью 12 км/ч. Доехав до города, велосипедист сразу повернул назад. На каком расстоянии от поселка он встретит пешехода?
   
   
4. Из столицы к лагерю на берегу реки выехала карета со скоростью 240 м/мин. Через полчаса навстречу карете из лагеря выехал всадник со скоростью 270 м/мин и встретил карету через 15 минут после выезда. Каково расстояние между лагерем и столицей?
   
   
5. Маша объявила, что умеет бегать от Медведя со скоростью 50м/мин. Медведь покачал головой: на самом деле Маша всё перепутала и думала, что в метре 80см, а в минуте 100секунд. С какой скоростью (см/сек) бегает Маша?
   
   
6. Из двух городов, расстояние между которыми 40 км, выехали в одном направлении грузовой и легковой автомобили. Скорость грузового 50 км/ч, скорость легкового 70 км/ч. Догонит ли легковая машина грузовую за 2 часа?
   
   
7. Две машины, расстояние между которыми 355 км, едут навстречу друг другу. Скорость первой машины 50 км/ч, а второй — 60 км/ч. Вторая машина сделала до встречи остановку на 30 минут. Через какое время машины встретятся? На каком расстоянии от места выезда второй произойдёт встреча?
   
   
8. Почтальон должен был проехать расстояние между двумя пунктами, равное 600 км, со скоростью 40 км/ч, но в дороге он вынужден был задержаться на 4 часа. Чтобы прибыть вовремя на место назначения, он должен после остановки увеличить свою скорость в 2 раза. На каком расстоянии от начала движения произошла задержка?

Дроби

1. Для Ильи Муромца выковали кольчугу. Кольчугу сковали из множества маленьких колец. На рукава пошла третья часть всех колец, по 1583 на каждый. Сколько всего колец выковали кузнецы для кольчуги Ильи Муромца?
   
   
2. Маленький Водяной любил съезжать с мельничного колеса. В один из дней он съехал с колеса 1050 раз. Седьмую часть всех поездок он совершил на животе, третью часть — на спине, а четвёртую часть оставшихся — на лопатках. Все остальные поездки он совершил на боку. Сколько раз Маленький Водяной съехал на боку?
   
   
3. Самуэль и Даниэль нарисовали два отрезка. Пятая часть отрезка Самуэля равна седьмой части отрезка Даниэля. У кого отрезок длиннее?
   
   
4. У Маши есть апельсины и яблоки. Известно, что 12 яблок составляют \( \dfrac{2}{5} \) части от всех Машиных фруктов. Сколько всего фруктов у Маши?
   
   
5. В сортировочный зал Главпочтамта поступило 3648 писем. До обеда отправили по назначению четверть всех писем, а после обеда — в два раза больше. Остальные письма оставили на завтра. Сколько писем осталось на завтра?
   
   
6. Винни-Пух и Пятачок вместе съели горшок мёда. Винни Пух съел две третьих мёда, а пятачок — 300 г. Сколько мёда было в горшке?

Деление с остатком

1. Миша живёт в 290 квартире в 9 этажном доме. На каждом этаже этого дома 4 квартиры. В каком подъезде живёт Миша?
   
   
2. Гоша живет в первом подъезде в квартире 31, а Витя живет в том же доме, в 3 подъезде в квартире 65, Гоша живет выше Вити. Сколько квартир в одном подъезде этого дома, если известно, что все подъезды одинаковые, и на каждой лестничной клетке расположено одно и то же количество квартир, причем на каждом этаже располагается больше одной квартиры?
   
   
3. Малыш живёт в 4 подъезде, в 34 квартире, а его друг Кристер — в 29 квартире, в третьем подъезде. Фрекен Бок переехала в квартиру 89. В каком подъезде теперь живёт Фрекен Бок? (Все подъезды и все этажи устроены одинаково.)
   
   
4. * Карлсон загадал число. Если это число поделить на 5, то получится минимально возможный ненулевой остаток, а если поделить на 7, то получится максимально возможный остаток. Какое число загадал Карлсон, если оно больше 50, но меньше 100?
   
   
5. Егор купил несколько луковиц тюльпанов и решил посадить их на грядки. Когда он стал сажать по 7 луковиц на грядку, то 1 луковица была лишняя. Он попробовал посадить по 6 луковиц, но одна снова была лишней. В третий раз он посадил по 13 луковиц на каждую грядку и все поместились. Сколько луковиц купил Егор, если их точно было меньше 200?

Геометрия

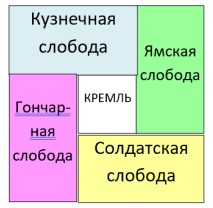
1. Территория кремля — квадрат. Вплотную к кремлю примыкают территории четырёх слобод, одинаковых по размеру (см. рис.). Территория каждой слободы — прямоугольник, у которого длина в два раза больше ширины. Найдите длину крепостных стен по периметру кремля, если известно, что площадь каждой слободы равна 32 км².
   
   
   
2. От квадрата отрезали четыре одинаковых равнобедренных треугольника как на рисунке:
   
   
   Какова площадь исходного квадрата, если площадь одного треугольника равна 128 см²?
   
   
3. Карлсон выяснил, что дом Малыша, дом Кристера и их школа расположены в вершинах равнобедренного треугольника. При этом Малыш сосчитал, что расстояние между его домом и домом Кристера 1 км 20 м, а расстояние от Кристера до школы 508 м. Чему равно расстояние от школы до дома Малыша? Равнобедренный треугольник — это треугольник, у которого есть две равные по длине стороны.
   
   
4. У Табиты есть золотая прямоугольная плитка. Табита отрезала от неё квадрат со стороной, равной одной из сторон прямоугольника и подарила его Саймону. Затем от получившегося прямоугольника она отрезала квадрат с другой стороны этого прямоугольника, и подарила его Питеру. После того, как Табита отрезала такой квадрат в третий раз и подарила его Пепелоце, у неё остался золотой квадрат площадью 4 см². Какого размера была исходная плитка?
   
   
5. Какой длины шпагат нужно взять, чтобы перевязать 10 пачек писем посылку размером 30 см × 20 см × 10 см, если известно, что на узел уходит 10 см шпагата?
   
   
6. Длина прямоугольника 43 см, а ширина 30 см меньше. Найдите периметр и площадь прямоугольника.
   
   
7. Обезьяна и 9 попугаев решили измерить длину удава. После проведённых измерений оказалось, что длина удава равна 36 попугаям или 9 обезьянам. Какова настоящая длина удава (в сантиметрах), если длина 1 обезьяны 75 см и длина попугая?

Разные задачи

1. Трамвай ходит по круговому маршруту, на котором только 4 остановки — Альфа, Бета, Гамма, Дельта. Однажды путешественник ехал в трамвае с местными жителями и спросил, когда будет станция Альфа. Ему с готовностью ответили:
   
   Баба Маня: «Та остановка, на которой ты зашел, — первая после Альфы».
   
   Баба Валя: «Да нет, ты все путаешь! Альфа была после Гаммы. А зашел он на Бете»
   
   Баба Яна: «Вы обе неправы! Гамма и Дельта — соседние остановки!»
   
   Баба Галя: «Как раз на Альфе-то он и вошел!»
   
   \medskip Как потом выяснилось, все утверждения бабушек про остановки и путешественника оказались неверными. Можете ли вы определить, в каком порядке идут остановки на маршруте и на какой остановке вошел путешественник?
   
   
2. В ящике лежат 25 синих кубиков, 12 красных и 7 зелёных. Какое минимальное количество кубиков нужно вынуть, не глядя, чтобы наверняка вытащить:
   
   
   • А) два кубика одного цвета;
   • Б) 8 кубиков одного цвета;
   • В) 3 кубика разных цветов?
   
   
   
3. Вика, Андрей и Гриша задумали три числа с разными цифрами: трёхзначное, четырёхзначное и пятизначное. Оказалось, что у числа Гриши все цифры нечётные и оно в 15 раз больше числа Вики. Найдите все три числа, если известно, что сумма чисел Вики и Гриши равна числу Андрея.
   
   
4. Какие из приведённых ниже утверждений являются истинными, а какие — ложными:
   • А) При делении числа на 8 не может получиться остаток 15;
   • Б) Если число делится на 6 и на 4, то оно обязательно делится на 24;
   • В) При делении на 56 в остатке может получиться 0;
   • Г) Если число делится на 2 и на 5, то оно делится на 10;
   • Д) Если число делится на 12 и на 10, то оно делится на 120;
   • Е) Если число делится на 5 с остатком 7 и на 7 — с остатком 5, то при делении этого числа на 5 в частном получится 7;
   • Ж) Число делится на 5 в частном получится 7;
   
   
   
5. Некоторое число поделили на 31 и получили частное 29 и какой-то остаток. Потом это же число поделили на 30 и получили частное 28 и тот же остаток. Что это было за число?
   
   
6. Карлсон может есть банку варенья за 10 минут, а Малыш — за 40. За какое время они смогут съесть эту банку вместе? (Предварительный вопрос: какую часть банки они съедят за 1 мин?)

Решения задач

1. Восстановите скобки:
   • \(78 + 102 - 75 \cdot 12\)
     Решение: Верное выражение: \(78 + (102 - 75) \cdot 12 = 78 + 27 \cdot 12 = 78 + 324 = 402\).
     Ответ: 402.
   • \(111 + 22 - 3 \cdot 55 - 15\)
     Решение: Верное выражение: \((111 + 22 - 3) \cdot 55 - 15 = 130 \cdot 55 - 15 = 7150 - 15 = 7135\).
     Ответ: 7135.
2. Вычислите:
   • \((287\,129 - 229\,856) + (872\,109 - 734\,075)\)
     Решение: \(57\,273 + 138\,034 = 195\,307\)
     Ответ: \(195\,307\).
   • \(76\,563\,001 - (123\,789 + 803\,005) - (890\,444 - 283\,917)\)
     Решение: \(76\,563\,001 - 926\,794 - 606\,527 = 75\,029\,680\)
     Ответ: \(75\,029\,680\).
   • \(90\,000 - 205 \cdot 409 - 156\,738 : 519 + 247\)
     Решение: \(90\,000 - 83\,845 - 302 + 247 = 6\,100\)
     Ответ: \(6\,100\).
   • \(849 \cdot (32\,207 : 301 + 74\,160 : 4120) \cdot 4\)
     Решение: \(849 \cdot (107 + 18) \cdot 4 = 424\,500\)
     Ответ: \(424\,500\).
   • \((701 \cdot 352 - 6148 : 58) : 2 - 323\)
     Решение: \((246\,752 - 106) : 2 - 323 = 123\,000\)
     Ответ: \(123\,000\).
   • \(167 \cdot (5047 : 49 + 8232 : 56) \cdot 4\)
     Решение: \(167 \cdot (103 + 147) \cdot 4 = 167\,000\)
     Ответ: \(167\,000\).
   • \((205 \cdot 104 - 74\,601 : 243) \cdot 5 + 5005\)
     Решение: \((21\,320 - 307) \cdot 5 + 5\,005 = 110\,070\)
     Ответ: \(110\,070\).
   • \(183 \cdot (1677 : 43 - 888 : 12 : 2) \cdot 50\)
     Решение: \(183 \cdot (39 - 37) \cdot 50 = 18\,300\)
     Ответ: \(18\,300\).
3. Сравните без вычислений:
   • \(764\,479 + 805\,691 = 705\,499 + 864\,671\)
     Ответ: Равны.
   • \(567 \cdot 9800 < 5760 \cdot 980\)
     Ответ: Второе больше.
   • \(678\,678\,678 : 678 < 678\,678\,678 : 113\)
     Ответ: Второе больше.
   • \(789\,453\,204 - 267\,892\,542 > 767\,453\,544 - 289\,892\,202\)
     Ответ: Первое больше.
4. Цифры вместо звёздочек:
   • А) \(57{*}8 > 5787\): \(8\) или \(9\)
     
   • Г) \(2{*}2 > 282\): \(9\)
     
5. Решите уравнение:
   • \((3891 - x \cdot 2) + 25419 = 27090\)
     Решение: \(3891 - 2x = 1671 \quad\Rightarrow\quad x = 1110\)
     Ответ: \(1110\).
   • \(100001 - (150 \cdot x + 44864) = 31587\)
     Решение: \(150x = 23550 \quad\Rightarrow\quad x = 157\)
     Ответ: \(157\).
6. Время прибытия Егора:
   Решение: \(7:00 + 50\ мин + 7\ мин + 45\ мин + 20\ мин + 30\ мин + 5\ мин + 33\ мин = 10:10\)
   Ответ: \(10:10\).
7. Стоимость пирожного:
   Решение: \(4x - 100 + 250 = 5x \quad\Rightarrow\quad x = 150\)
   Ответ: \(150\) руб.
8. Стоимость обложки:
   Решение: \(Б + О = 20\), \(Б = О + 18 \quad\Rightarrow\quad О = 1\)
   Ответ: \(1\) руб.
9. Оплата группой:
   Решение: \(25 \cdot 200 + 2 \cdot 400 = 5800\)
   Ответ: \(5800\) руб.
10. Стоимость блокнота:
    Решение: \(8 \cdot 180 = 1440 \quad\Rightarrow\quad 1440 : 9 = 160\)
    Ответ: \(160\) руб.
11. Стоимость 5 арбузов:
    Решение: \(A = D - 40\), \(2(A + D) = 420 \quad\Rightarrow\quad A = 85\), \(5A = 425\)
    Ответ: \(425\) руб.
12. Молотки:
    Решение: \(C + Са = 588\), \(Ст + Са = 766 \quad\Rightarrow\quad Ст = 502\), \(Са = 264\), \(С = 324\)
    Ответ: \(324\), \(502\), \(264\).
13. Распределение тетрадей:
    Ответ: Коля \(-\) \(27\), Вася \(-\) \(25\), Юра \(-\) \(18\), Саша \(-\) \(16\), Сережа \(-\) \(14\).
14. Время встречи пешехода и велосипедиста:
    Решение: Велосипедист проезжает \(48\) км за \(4\) часа. Пешеход к этому моменту проходит \(16\) км. Встреча через \(2\) часа после разворота: \(16 + 4 \cdot 2 = 24\) км.
    Ответ: \(24\) км.