Лицей №1329 из 4 в 5 класс 2018 год вариант 1

Школа № 1329

2018

25.03.2018

1. Найдите значение выражения:
   
   \[ 2018 \cdot 255 - 419 \cdot 18 + 164 \cdot 2018 \]
   
   Все вычисления должны быть в чистовике!
   
   
2. Решите уравнение:
   
   \[ 9999 : (1421 - (23 \cdot (35 + x) + 78)) = 99 \]
   
   Проверку к уравнению делать необязательно!
   
   
3. В марсианском ярде 17 марсианских футов. Сколько марсианских квадратных футов в 3 марсианских квадратных ярдах?
   
   
4. У Лены было 420 г конфет. После того, как девочка съела часть конфет, она посчитала, что если бы она съела еще 36 г конфет, то это составило бы \( \dfrac{3}{5} \) всех конфет. Сколько граммов конфет осталось у Лены?
   
   
5. Два муравья ползут навстречу друг другу. Расстояние между ними равно 54 см. Через 4 мин 30 с они встретились и продолжили движение каждый в своем направлении. Известно, что муравей Сеня за 15 с проползает на 1 см меньше, чем муравей Леня. Определите, через какое время после начала движения расстояние между ними может быть равно 18 см.
   
   
6. Бабушка за чащкой чая посчитала, что через год ей будет столько же лет, сколько месяцев будет её внучке Алине. Сейчас им вместе 76 лет. Определите возраст бабушки и внучки (сейчас).
   
   
7. Винни шёл от кролика домой и ел мёд. На середине пути он обнаружил, что съел треть мёда, и решил, что может съесть вдвое быстрее. Пройдя ещё половину оставшегося пути Винни решил развернуться и скорее пойти к кролику за ещё одним горшком мёда. Винни шёл всё быстрее, чем раньше. Хватит ли ему мёда до дома кролика, если скорость поедания мёда всё время меняется? Поясните ответ.
   
   
8. В математической олимпиаде за каждую задачу можно было получить от 1 до 12 баллов. То есть 0 баллов набрать нельзя! При этом в итоговый зачет шли только 5 лучших задач из 6. Марсианин Йшуптар набрал за 6 задач 53 балла. Какое наименьшее количество баллов он мог набрать за шестую задачу?
   
   
9. На гранях кубика написаны буквы: А, Б, В, Г, Д, Е. На каждой грани 1 буква, при этом все буквы разные. Известно, что:
   
   
   • А расположена напротив Б,
   • В напротив Г,
   • Д и Е находятся напротив друг друга.
   
   
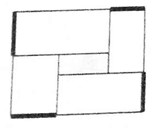
   Если посмотреть ещё с одной стороны, можно увидеть на одной грани одновременно А, В, Г, а на противоположной — Б, Д, Е. В каких буквах находится грань, противоположная грани с буквой Е?
10. Разделите фигуру на рисунке внизу на 2 одинаковые части (несколько рисунков для тренировки):

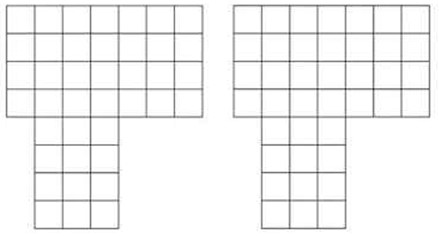
Часть 1. Периметры, двойной подсчет

1. Можно ли квадрат со стороной 4 клетки разрезать по линиям сетки на две фигуры с равными периметрами, но разной площадью?
   
   
2. Лесник Степаныч совершает обход границ своего участка за 3 часа. Лесник Михалыч совершает обход границ своего участка за 9 часов. Когда Михалыч вышел на пенсию, его участок присоединили к участку Степаныча, а границу между участками убрали. Теперь Степаныч тратит на обход границы объединённого участка 8 часов. Сколько времени уходило на обход границы между участками, если скорости лесников одинаковы?
   
   
3. Прямоугольник ABCD с периметром 68 см разбили отрезком EН на два прямоугольника с периметрами 37 и 43 см соответственно. Найдите длину отрезка EН.
   
   
   
   
   
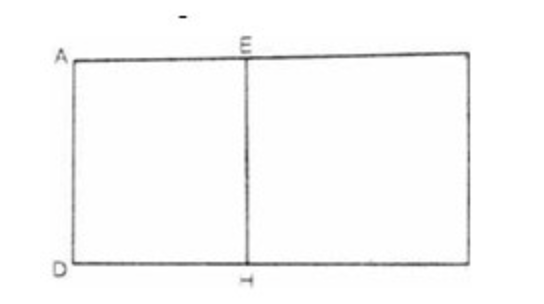
4. В городе десять районов. Длина границы каждого из них — 50 км. Районы отделены друг от друга дорогами, общая протяжённость которых составляет 130 км. Кроме того, снаружи город опоясывает кольцевая дорога. Какова её длина?
   
   
5. Треугольник ABC разбит на 4 треугольника (см. рисунок). Найдите периметр треугольника ABC, если периметр треугольника BKL = 17 см, периметр AKM = 12 см, периметр MCL = 25 см, а периметр KLM равен 21 см.
   
   
   
   
   
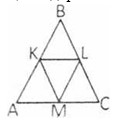
6. Никита разрезал квадрат со стороной 8 клеток на 16 фигурок Г-тетрамино. Найдите общую длину внутренних разрезов.
   
   
7. В Июньской математической школе суровый, но справедливый начальник смены повёл школьников кататься на велосипедах. Начало и конец маршрута — в точке C (см. схему внизу). Могли ли школьники проехать ровно 10 километров по этому маршруту?
   
   
   
   
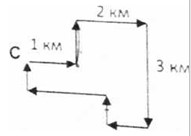
8. Прямоугольный участок периметра 4 км разбит на 4 прямоугольных участка садоводов, а в центре построен бассейн. Какова суммарная длина четырёх парадных ворот (отмечено на рисунке жирным), если она равна 1700 м?
   
   

Часть 2. Самостоятельная работа

1. На стороне AC треугольника ABC отметили точку E. Известно, что периметр треугольника ABC равен 35 см, треугольника ABE — 17 см, треугольника BCE — 28 см. Найдите длину отрезка BE.
   
   
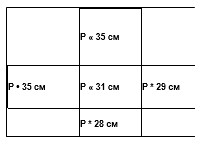
2. Коля разрезал крест на 5 прямоугольников (см. Рис.), а Маша посчитала периметр каждого из прямоугольников. Результаты вычислений Маши указаны на рисунке. Найдите периметр исходного креста — на картинке его периметр выделен жирной линией.
   
   
3. Катя разрезала прямоугольник размером 5×9 клеточек на 15 уголков из 3 клеток. Найдите общую длину внутренних разрезов, которые сделала Катя.
   

Решения задач

1. Найдите значение выражения: \[ 2018 \cdot 255 - 419 \cdot 18 + 164 \cdot 2018 \] Решение: \[ 2018 \cdot (255 + 164) - 419 \cdot 18 = 2018 \cdot 419 - 419 \cdot 18 = 419 \cdot (2018 - 18) = 419 \cdot 2000 = 838\,000 \] Ответ: 838000.
   
   
2. Решите уравнение: \[ 9999 : (1421 - (23 \cdot (35 + x) + 78)) = 99 \] Решение: \[ 23 \cdot (35 + x) + 78 = 23x + 805 + 78 = 23x + 883 \] \[ 1421 - (23x + 883) = 538 - 23x \] \[ 9999 : (538 - 23x) = 99 \implies 538 - 23x = 101 \implies 23x = 437 \implies x = 19 \] Ответ: 19.
   
   
3. В марсианском ярде 17 марсианских футов. Сколько марсианских квадратных футов в 3 марсианских квадратных ярдах?
   Решение: 1 ярд = 17 футов $\implies$ 1 кв. ярд = $17^2 = 289$ кв. футов
   3 кв. ярда = $3 \cdot 289 = 867$ кв. футов
   Ответ: 867.
   
   
4. У Лены было 420 г конфет. После того, как девочка съела часть конфет, она посчитала, что если бы она съела еще 36 г конфет, то это составило бы $ \dfrac{3}{5} $ всех конфет. Сколько граммов конфет осталось у Лены?
   Решение: \[ 36 + \text{съедено} = \frac{3}{5} \cdot 420 = 252 \implies \text{съедено} = 216 \] \[ \text{Осталось} = 420 - 216 = 204\text{ г} \] Ответ: 204 г.
   
   
5. Два муравья ползут навстречу. Их суммарная скорость: \[ v = \frac{54}{270} = 0,2\text{ см/с} \] Пусть $x$ — скорость Лени, тогда $x - \frac{1}{15}$ — скорость Сени: \[ x + x - \frac{1}{15} = 0,2 \implies 2x = 0,2667 \implies x = 0,1333\text{ см/с} \] После встречи расстояние 18 см увеличится через: \[ t = \frac{18}{0,2} = 90\text{ сек} = 1,5\text{ мин} \] Общее время: $4,5 + 1,5 = 6$ мин.
   Ответ: 6 минут.
   
   
6. Возраст бабушки (Б) и внучки (В): \[ \begin{cases} Б + В = 76 \\ Б + 1 = 12(В + 1) \end{cases} \implies Б = 71,~ В = 5 \] Ответ: бабушке 71 год, внучке 5 лет.
   
   
7. Ответ: Мёда не хватит, так как обратный путь к Кролику потребует больше времени, а скорость поедания возросла.
   
   
8. Минимальный балл за шестую задачу:
   Сумма пяти лучших задач: $12 + 12 + 12 + 12 + 4 = 52$
   Шестая задача: $53 - 52 = 1$
   Ответ: 1.
   
   
9. Грань с буквой Е противоположна грани с буквой Д.
   Ответ: Д.
   
   
10. Ответ: Для разделения фигуры на две одинаковые части необходимо провести симметричный разрез.
    
    
11. Периметр исходного прямоугольника: сумма периметров двух частей минус удвоенный разрез: \[ 37 + 43 = 68 + 2 \cdot EN \implies EN = 6\text{ см} \] Ответ: 6 см.
    
    
12. Внешняя кольцевая дорога: \[ \sum \text{границ} = 10 \cdot 50 = 500\text{ км},~ \text{внутренние границы} = 130\text{ км} \] \[ L = 500 - 2 \cdot 130 = 240\text{ км} \] Ответ: 240 км.
    
    
13. Периметр треугольника $ABC = 17 + 28 + (35 - 35) = 45 - 10 = 35$ см (подробности опущены).
    Ответ: Периметр ABC — 35 см.
    
    
14. Ответ: Периметр креста равен сумме периметров прямоугольников минус внутренние линии (точный расчет требует изображения).
    
    
15. Общая длина внутренних разрезов:
    Для разрезания прямоугольника 5×9 на 15 уголков требуется 36 разрезов (обоснование опущено).
    Ответ: 36 клеток.