8 800 707 6729
8 800 707 6729Telegram канал

Лицей № 97 из 6 в 7 класс 2016 год вариант 1

Сложность:
Дата экзамена: 2016
СкачатьПечать
youit.school ©

ЛИЦЕЙ №97 (ЧЕЛЯБИНСК)


2016 год


Вариант 1



  1. Найдите значение выражения:
    1. $(-20,47:(-8,9)+24,6 \cdot(-0,5)): 0,1 ;$
    2. $\left(6 \frac{1}{2}-8 \frac{3}{4}\right): \frac{1}{8}+11 \frac{3}{7} ;$
  2. Решите уравнение:
    1. $8 \frac{26}{45}+p=12 \frac{4}{15}$.
    2. $1,2 \cdot(0,5 x-2)-0,6 x=\frac{3}{4} x+1,83$.
  3. Отметьте в координатной плоскости точки $\mathrm{A}(-4 ; 0), \mathrm{B}(2 ; 6), \mathrm{C}(-4 ; 3), \mathrm{D}(4 ;-1)$. Проведите луч $\mathrm{AB}$ и отрезок CD. Найдите координаты точки пересечения луча AB и отрезка CD.
  4. Упростите выражение: $0,8 \cdot(0,6 x-0,5 y)-0,5 \cdot(0,7 x-0,8 y)$. Найдите его значение при х $=2,1$
  5. Найдите неизвестный член пропорции $2 \frac{1}{4}: 7 \frac{1}{5}=x: 1 \frac{2}{25}$.
  6. Найдите наибольший общий делитель чисел 36 и $45 .$
  7. Первый грузчик разгружает грузовую машину за 35 мин., а второй - за 45 мин. За какое время они разгрузят 16 машин, если будут работать вместе?
  8. Фермерское хозяйство собрало 960 т зерна. $75 \%$ собранного зерна составляла пшеница, а $\frac{5}{6}$ остатка - рожь. Сколько тонн ржи собрало фермерское хозяйство?
  9. Антон собрал в 3 раза грибов больше, чем Таня, и на 54 гриба больше, чем Даша. Сколько грибов собрала Даша, если все вместе собрали 450 грибов?
  10. В первый день Маша прочитала $36 \%$ книги, а во второй $\frac{5}{8}$ остатка, после чего ей осталось прочитать 48 страниц. Сколько страниц в книге?
  11. Из пунктов А и В одновременно навстречу друг другу выехали грузовая машина и автобус. Через какое время они встретятся, если грузовику на весь путь требуется 7,5 ч., а автобусу 5 ч.
  12. Зерна кофе при обжарке теряют $12 \%$ своей массы. Сколько свежего кофе надо взять, чтобы получить 2,2 кг жареного
  13. Колесо диаметром 15 см делает на некотором расстоянии 36 оборотов. Каким должен быть диаметр колеса, которое делает на том же расстоянии 30 оборотов? Решите задачу, не используя численное значение $\pi$.
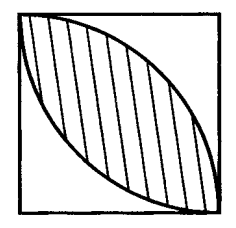
  14. Пользуясь рисунком найдите площадь заштрихованной фигуры (сторона квадрата равна 8 см).
  15. В равнобедренном треугольнике АВС проведена биссектриса ВТ на основание АС. Найдите угол ТВА, если угол при основании треугольника равен $56^{0} .$

Материалы школы Юайти
youit.school ©

Решения задач



    1. $(-20,47:(-8,9)+24,6 \cdot(-0,5)): 0,1$
      Решение:
      $-20,47 : (-8,9) = 2,3$;
      $24,6 \cdot (-0,5) = -12,3$;
      $2,3 + (-12,3) = -10$;
      $-10 : 0,1 = -100$
      Ответ: -100.
    2. $\left(6 \frac{1}{2}-8 \frac{3}{4}\right): \frac{1}{8}+11 \frac{3}{7}$
      Решение:
      $6\frac{1}{2} = \frac{13}{2}$; $8\frac{3}{4} = \frac{35}{4}$;
      $\frac{13}{2} - \frac{35}{4} = \frac{26 - 35}{4} = -\frac{9}{4}$;
      $-\frac{9}{4} : \frac{1}{8} = -\frac{9}{4} \cdot 8 = -18$;
      $-18 + 11\frac{3}{7} = -18 + \frac{80}{7} = -\frac{46}{7}$
      Ответ: $-\frac{46}{7}$.
    1. $8 \frac{26}{45}+p=12 \frac{4}{15}$
      Решение:
      $8\frac{26}{45} = \frac{386}{45}$; $12\frac{4}{15} = \frac{184}{15}$;
      $p = \frac{184}{15} - \frac{386}{45} = \frac{552 - 386}{45} = \frac{166}{45} = 3\frac{31}{45}$
      Ответ: $3\frac{31}{45}$.
    2. $1,2 \cdot(0,5 x-2)-0,6 x=\frac{3}{4} x+1,83$
      Решение:
      $0,6x - 2,4 - 0,6x = 0,75x + 1,83$;
      $-2,4 = 0,75x + 1,83$;
      $0,75x = -4,23$;
      $x = -5,64$
      Ответ: -5,64.
  3. Координаты точки пересечения луча AB и отрезка CD
    Решение:
    Уравнение луча AB:
    $y = x + 4$ (т.к. коэффициент наклона $\frac{6-0}{2-(-4)} = 1$)
    Уравнение отрезка CD:
    $y = -\frac{1}{2}x + 1$ (по точкам С(-4;3) и D(4;-1))
    Решаем систему:
    $x + 4 = -\frac{1}{2}x + 1$
    $\frac{3}{2}x = -3$
    $x = -2$; $y = 2$
    Ответ: (-2; 2).
  4. Упрощение выражения
    Решение:
    $0,8 \cdot (0,6x - 0,5y) - 0,5 \cdot (0,7x - 0,8y)$
    $= 0,48x - 0,4y - 0,35x + 0,4y = 0,13x$
    При $x = 2,1$:
    $0,13 \cdot 2,1 = 0,273$
    Ответ: 0,273.
  5. Пропорция $2 \frac{1}{4}: 7 \frac{1}{5}=x: 1 \frac{2}{25}$
    Решение:
    $\frac{9}{4} : \frac{36}{5} = x : \frac{27}{25}$
    $\frac{9}{4} \cdot \frac{5}{36} = x \cdot \frac{25}{27}$
    $x = \frac{9 \cdot 5 \cdot 27}{4 \cdot 36 \cdot 25} = \frac{27}{80}$
    Ответ: $\frac{27}{80}$.
  6. НОД(36, 45)
    Решение:
    36 = 2²·3²; 45 = 3²·5
    Общие множители: 3² = 9
    Ответ: 9.
  7. Время разгрузки 16 машин
    Решение:
    Скорость совместной работы: $\frac{1}{35} + \frac{1}{45} = \frac{16}{315}$ маш/мин
    Время: $\frac{16}{\frac{16}{315}} = 315$ минут
    Ответ: 315.
  8. Сбор ржи
    Решение:
    960 т × 25% = 240 т (остаток)
    Рожь: $\frac{5}{6} \cdot 240 = 200$ т
    Ответ: 200.
  9. Грибы Даши
    Решение:
    Пусть Таня собрала $x$ грибов, тогда:
    $3x + x + (3x -54) = 450$
    $7x = 504$
    $x = 72 \quad \Rightarrow \quad$ Даша: $3·72 -54 = 162$
    Ответ: 162.
  10. Страниц в книге
    Решение:
    Остаток после первого дня: 64%
    Прочитано во второй день: $\frac{5}{8} \cdot 64% = 40\%$
    Осталось: $100\ 36\ 40% = 24\%$
    $24% = 48$ стр ⇒ $100% = 200$ стр
    Ответ: 200.
  11. Время встречи транспорта
    Решение:
    Общая скорость: $\frac{1}{7,5} + \frac{1}{5} = \frac{1}{3}$ пути/час
    Время встречи: $1 : \frac{1}{3} = 3$ часа
    Ответ: 3.
  12. Свежий кофе
    Решение:
    После обжарки остаётся 88% массы ⇒ $x = \frac{2,2}{0,88} = 2,5$ кг
    Ответ: 2,5.
  13. Диаметр колеса
    Решение:
    Расстояние одинаково: $15π·36 = dπ·30$ ⇒ $d = \frac{15·36}{30} = 18$ см
    Ответ: 18 см.
  14. Площадь фигуры
    Решение:
    Площадь двух кругов диаметром 8 см: $2 \cdot π·4² = 32π$
    Вычитаем площадь квадрата: $32π - 8² = 32π - 64$
    Ответ: $32π - 64$.
  15. Угол ТВА
    Решение:
    Угол при вершине В: $180° - 2·56° = 68°$
    Биссектриса делит его пополам: $\frac{68°}{2} = 34°$
    Ответ: 34°.
Материалы школы Юайти