Лицей № 1525 «Воробьевы Горы» из 8 в 8 класс 2025 год

1. Найдите значение выражения: \[ (\sqrt{13} - 2)(\sqrt{13} + 2) \]
2. Решите уравнение: \[ x^4 = (x-2)^2 \]
3. Какие целые числа расположены между $\sqrt{6}$ и $\sqrt{62}$.
4. Диагональ прямоугольника образует угол $51^\circ$ с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника.
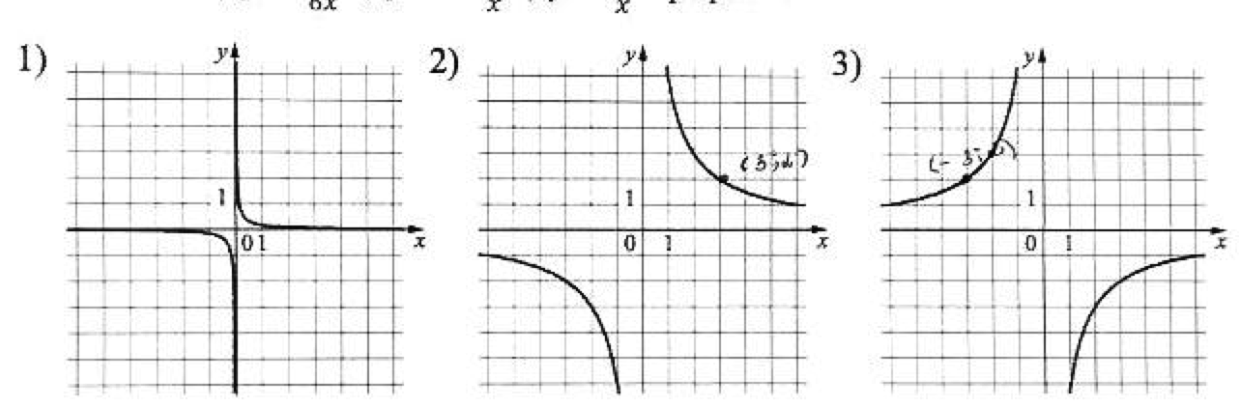
5. Установите соответствие между функциями и их графиками. Функции: а) $y = \dfrac{6}{x}$ $\quad$б) $y = -\dfrac{1}{x}$ $\quad$ в) $y = \dfrac{6}{x^2}$ Графики:
   
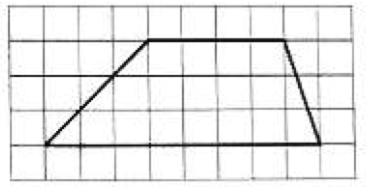
6. На клетчатой бумаге с размером клетки $1 \times 1$ изображена трапеция. Найдите её площадь.
   
7. Через точку $O$ пересечения диагоналей параллелограмма $ABCD$ проведена прямая, пересекающая стороны $AB$ и $CD$ в точках $E$ и $F$ соответственно. Докажите, что отрезки $AE$ и $CF$ равны.
8. На клетчатой бумаге с размером клетки $1 \times 1$ нарисована «змейка», представляющая из себя ломаную, состоящую из чётного числа звеньев, каждое из которых имеет длину 1. Нарисуйте изображённую змейку, когда последнее звено имеет длину 10. Найдите длину ломаной, построенной аналогичным образом, последнее звено которой имеет длину 110.
   

Решения задач

1. Найдите значение выражения: \[ (\sqrt{13} - 2)(\sqrt{13} + 2) \] Решение: Воспользуемся формулой разности квадратов: \[ (\sqrt{13})^2 - 2^2 = 13 - 4 = 9 \] Ответ: 9.
2. Решите уравнение: \[ x^4 = (x-2)^2 \] Решение: Перенесём все слагаемые в левую часть: \[ x^4 - (x-2)^2 = 0 \quad \Rightarrow \quad (x^2 - (x-2))(x^2 + (x-2)) = 0 \] Решаем уравнения по отдельности:
   • $x^2 - x + 2 = 0$ — дискриминант $D = (-1)^2 - 8 = -7 < 0$, корней нет.
   • $x^2 + x - 2 = 0$ — корни $x = 1$ и $x = -2$.
   Проверка показывает, что оба корня удовлетворяют исходному уравнению.
   Ответ: $1; -2$.
3. Какие целые числа расположены между $\sqrt{6}$ и $\sqrt{62}$.
   Решение: Оценим значения корней: \[ \sqrt{6} \approx 2,45; \quad \sqrt{62} \approx 7,87 \] Целые числа между ними: $3, 4, 5, 6, 7$.
   Ответ: 3, 4, 5, 6, 7.
4. Диагональ прямоугольника образует угол $51^\circ$ с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника.
   Решение: Диагонали прямоугольника равны и делятся пополам. Угол между диагональю и стороной $51^\circ$, значит угол между диагоналями: \[ 180^\circ - 2 \cdot 51^\circ = 78^\circ \] Ответ: $78^\circ$.
5. Установите соответствие между функциями и их графиками.
   Решение:
   • $y = \dfrac{6}{x}$ — гипербола в I и III квадрантах (график А).
   • $y = -\dfrac{1}{x}$ — гипербола во II и IV квадрантах (график Б).
   • $y = \dfrac{6}{x^2}$ — график в виде "галочки" в верхней полуплоскости (график В).
   Ответ: А-а, Б-б, В-в.
6. На клетчатой бумаге с размером клетки $1 \times 1$ изображена трапеция. Найдите её площадь.
   Решение: Основания трапеции равны 3 и 5 клеток, высота — 4 клетки: \[ S = \frac{3 + 5}{2} \cdot 4 = 16 \] Ответ: 16.
7. Через точку $O$ пересечения диагоналей параллелограмма $ABCD$ проведена прямая, пересекающая стороны $AB$ и $CD$ в точках $E$ и $F$ соответственно. Докажите, что отрезки $AE$ и $CF$ равны.
   Решение: Треугольники $\triangle AEO$ и $\triangle CFO$ равны по ASA (углы при вершине $O$ равны как вертикальные, $AO = OC$, углы при $A$ и $C$ равны как накрест лежащие). Следовательно, $AE = CF$.
   Ответ: Доказано.
8. На клетчатой бумаге с размером клетки $1 \times 1$ нарисована «змейка», состоящая из чётного числа звеньев длиной 1. Найдите длину ломаной, последнее звено которой имеет длину 110.
   Решение: Каждые два звена образуют "уголок", увеличивая длину последнего звена на 2. Для последнего звена 110 количество пар звеньев равно 110, общее количество звеньев: \[ 110 \cdot 2 = 220 \] Ответ: 220.