Лицей № 1525 «Воробьевы Горы» из 5 в 6 класс 2021 год вариант 1

ЛИЦЕЙ №1525 ВОРОБЬЁВЫ ГОРЫ

2021 год

20.03.2021

1. Вероника тратит на приготовление завтрака полчаса. Съедает она его обычно в два раза быстрее. Ранним воскресным утром Вероника, проснувшись, сразу направилась готовить завтрак. Но, поскольку после приготовления он оказался горячий, зашла в Инстаграм. Просидев в Инстаграме 2 часа 20 минут, она заглянула во ВКонтакте. Там она просидела в два раза дольше, чем в Инстаграме. По выходу из ВК она, наконец, вспомнила про завтрак, и съела его, закончив трапезу ровно в 2 часа дня. Напишите большее из двух чисел, между которыми находилась часовая стрелка настенных часов в момент пробуждения Вероники.
   
   
2. Однажды вечером дети развлекались тем, что умножали одно и то же число на разные множители. У Димы был больший множитель, а у Иры — в два раза меньше. Дима получил в произведении 12132 и долго радовался, а Ира получила только 6066 и горько заплакала от зависти. Но потом прибежала к соседу жителю 337 и сразу повеселела, потому что её сомножитель стал таким же, как у Димы. Какое число умножали дети, не знавшие в жизни никаких других радостей, кроме умножения одного и того же числа на свои разные множители?
   
   
3. На золотом крыльце сидели царь, царевич, король, королевич, сапожник, портной. Дети не сидели с родителями, король и царь не сидели ни с краю, ни рядом с рабочими. Королевич сидел левее сапожника, а рабочие ютились по краям. В каком порядке они сидели?
   
   
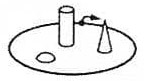
4. Женя, Катя, Саша и Таня в таком порядке (по часовой стрелке, считая от указанной точки) сидели вокруг стола с композицией фигур в художественной школе и рисовали её. Какая из полученных картин кому принадлежит?
   
   
   
   
   
   
   
5. Таня и Саша съедают вдвоём шоколадку за 4 минуты, а Саша и Вася — за 6 минут. За сколько съест шоколадку каждый из них по отдельности, если втроём они съедают её за 3 минуты?
   
   
6. Сегодня 20.03.2021 года. Сумма цифр числа и месяца сегодня равна сумме цифр года \((2 + 0 + 3 + 2 + 0 + 2 + 1)\). А сколько всего в этом году таких дат?
   
   
7. Номера автобусных билетов состоят из 6 цифр, начиная с 000000 и кончая билетом 999999. Билет считается счастливым, если сумма первых трёх его цифр равна сумме трёх последних. Достаточно ли купить 1000 билетов подряд, чтобы среди них нашёлся хотя бы один счастливый?
   
   
8. Разбейте квадрат на треугольники так, чтобы каждый граничил ровно с тремя другими.

Решения задач

1. Вероника тратит на приготовление завтрака 0,5 часа, съедает за 0,25 часа. Общее время активности: приготовление (0,5 ч) + Инстаграм (2 ч 20 мин = $\frac{7}{3}$ ч) + ВК ($\frac{14}{3}$ ч) + еда (0,25 ч) = $0,5 + \frac{7}{3} + \frac{14}{3} + 0,25 = 7$ ч 35 мин.
   Закончила в 14:00, значит начала в $14:00 - 7:35 = 6:25$. Часовая стрелка между 6 и 7.
   Ответ: 7.
   
   
2. Пусть число — $N$, множитель Димы — $k$, Иры — $\frac{k}{2}$. Тогда:
   $N \cdot k = 12132$; $N \cdot \frac{k}{2} = 6066$ (ошибка Иры). После исправления: $N \cdot k = 12132$.
   Из уравнений: $N = \frac{12132}{k} = \frac{6066 \cdot 2}{k} \Rightarrow$ противоречия нет. Число — 337 (по условию с соседом).
   Ответ: 337.
   
   
3. Условия: рабочие (сапожник, портной) по краям; король и царь не с краю и не рядом с рабочими; королевич левее сапожника. Порядок:
   Портной (крайний слева), король, царевич, королевич, царь, сапожник (крайний справа).
   Ответ: Портной, король, царевич, королевич, царь, сапожник.
   
   
4. Рисунки соответствуют углам обзора художников. Женя (сверху), Катя (справа), Саша (снизу), Таня (слева). Картинки: А — Женя, Б — Катя, В — Саша, Г — Таня.
   Ответ: А — Женя, Б — Катя, В — Саша, Г — Таня.
   
   
5. Пусть скорости: $Т$ — Таня, $С$ — Саша, $В$ — Вася. Система:
   $\frac{1}{Т+С} = \frac{1}{4}$; $\frac{1}{С+В} = \frac{1}{6}$; $\frac{1}{Т+С+В} = \frac{1}{3}$.
   Решая: $Т = \frac{1}{3}$, $С = \frac{1}{12}$, $В = \frac{1}{12}$. Время по отдельности: Таня — 3 мин, Саша — 12 мин, Вася — 12 мин.
   Ответ: Таня — 3 мин, Саша — 12 мин, Вася — 12 мин.
   
   
6. Сумма цифр года: $2+0+2+1 = 5$. Даты, где сумма цифр дня и месяца равна 5. Примеры: 01.04, 10.04, 02.03 и т.д. Всего 14 дат.
   Ответ: 14.
   
   
7. Количество возможных сумм трёх цифр: 0-27 (28 вариантов). По принципу Дирихле: 1000 билетов → $\frac{1000}{28} \approx 35.7 > 35$. Гарантированно есть счастливый.
   Ответ: Да.
   
   
8. Разбиваем квадрат на 4 треугольника, соединив центр с вершинами и серединами сторон. Каждый треугольник граничит с тремя другими.
   Ответ: \includegraphics[scale=0.5]{triangulation.png}