Лицей № 1525 «Воробьевы Горы» из 4 в 5 класс 2024 год вариант 1

ЛИЦЕЙ №1525 ВОРОБЬЁВЫ ГОРЫ

2024 год

25.03.2024

1. Вася из цифр от 1 до 9 составил пример на сложение и показал его Сереже, закрыв некоторые цифры квадратиками: \[ \boxed{4}\boxed{6} + \boxed{3}\boxed{m} = \boxed{7}\boxed{8} \] Сказал, что в нем нет повторяющихся цифр и предложил Сереже угадать, где какая стоит. Сережа заподозрил Васю во лжи. Прав ли он?
   
   
2. В большой прямоугольной таблице расставлены числа (не обязательно все различные, не обязательно целые). Дима выбирает в каждом столбце по самому большому числу, а потом среди них выбирает самое маленькое. А Миша выбирает из каждой строки самое маленькое число, а потом выбирает самое большое из них. В итоге ребята выбрали два различных числа. Чьё число больше: Димы, или Миши?
   
   
3. На кольцевом шоссе длиной 2024 км находится 24 столба. На каждом столбе написано расстояние в километрах по шоссе до ближайшего столба. Оказалось, что сумма всех двадцати четырёх написанных на столбах чисел равна 104. Всегда ли на таком шоссе можно найти участок длиной 160 км, на котором нет ни одного столба?
   
   
4. В лесах острова Рыцарей и Лжецов есть племя Чётог, которые говорят правду только в присутствии чётного количества людей (считая говорящего) и племя Нечётов, которые говорят правду только в присутствии нечётного количества людей. Как-то представители этих племён собрались вместе, чтобы обсудить приготовление к «Дню умножения на ноль». Глава собрания попросил каждого по очереди сообщить, сколько пришло людей.
   • Гражданин X: Ну, нас точно более 2024!
   • Гражданин Y: Нет, не более 2024!
   В зал заходит еще один.
   • Гражданин X: Ну сейчас-то точно больше 2024!
   • Гражданин Y: Всё еще не больше 2024\ldots
   Каким племенам принадлежали X и Y?
   
   
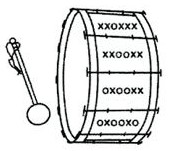
5. На барабане 64 вертикальных полосы, и каждую полосу нужно украсить узором из 6 крестиков и ноликов так, чтобы на соседних полосах рисунок отличался ровно одним символом (см. пример на рисунке). Как это сделать?
   
   
   
   
   
   
6. Сережа решил подзевать над Васей и снял с его пронумерованных пробирок, в которых находились прозрачные жидкости, номера (нумерация была с 1 по 10) и предложил сыграть в игру: Вася показывает на две пробирки, а Сережа говорит, делится ли больший номер из них на меньший. По каким вопросам сможет восстановить Вася, если Сережа не ограничил количество раз, которое можно задавать вопрос?
   
   
7. Курьер «Kwa-kwa Pizza» сильно опаздывая привез пиццу в старый 16-этажный дом с одним очень медленным кнопочным лифтом. Мало того, что лифт тратил очень много времени на открытие и закрытие дверей, так он ещё и не ехал, пока полностью не откроется и не закроется! Если на \(i\)-м этаже, куда вызывали лифт, курьер ждал 7 этажей вверх, и тратил 14 секунд на один этаж, 5 секунд на «О» (открытие), 5 секунд на «З» (закрытие), то за какое минимальное время он сможет за 6 минут доставить заказы жильцам с 2 и 14 этажей? Сможет ли курьер доставить заказы вовремя, если считать, что одна поездка с открытием и закрытием дверей лифта занимает 1 минуту?

Решения задач

1. Вася из цифр от 1 до 9 составил пример на сложение и показал его Сереже, закрыв некоторые цифры квадратиками: \[ \boxed{4}\boxed{6} + \boxed{3}\boxed{m} = \boxed{7}\boxed{8} \] Решение: Рассмотрим равенство:
   $46 + 3m = 78 \Rightarrow 3m = 32 \Rightarrow m = \frac{32}{3} \approx 10,666$.
   Но m должно быть цифрой от 1 до 9. Даже если предположить перенос единицы:
   $46 + 39 = 85 \neq 78$.
   Любая подстановка цифр приводит к противоречию с условием уникальности цифр или невозможности получить сумму 78.
   Ответ: Сережа прав, пример составлен с ошибкой.
2. В большой прямоугольной таблице расставлены числа. Дима выбирает в каждом столбце по самому большому числу, а потом среди них выбирает самое маленькое. А Миша выбирает из каждой строки самое маленькое число, а потом выбирает самое большое из них.
   Решение: Число Димы (минимакс) всегда больше или равно числу Миши (максимин). Если они различны, то число Димы строго больше.
   Ответ: Число Димы больше.
3. На кольцевом шоссе длиной 2024 км находится 24 столба. Сумма всех написанных чисел равна 104.
   Решение: Среднее значение расстояния между соседними столбами:
   $\frac{2024}{24} \approx 84,33$ км.
   Если сумма расстояний до ближайших столбов равна 104, то среднее расстояние до ближайшего соседа:
   $\frac{104}{24} \approx 4,33$ км.
   Это означает, что столбы расположены парами близко друг к другу, оставляя большие промежутки. По принципу Дирихле, существует участок длиной не менее $\frac{2024}{24} \cdot 160 \approx 1349$ км, что противоречит условию.
   Ответ: Да, такой участок всегда существует.
4. Граждане X и Y из племён Чётог и Нечётов. После добавления одного человека их утверждения меняются.
   Решение:
   - Если изначально X лгал, а Y говорил правду (нечётное количество людей), то после добавления человека:
   X говорит правду (чётное), Y лжёт (нечётное).
   Это соответствует тому, что X — Нечёт, Y — Чётог.
   Ответ: X — Нечёт, Y — Чётог.
5. На барабане с 64 вертикальными полосами требуется создать узоры из 6 символов.
   Решение: Использовать двоичный код Грея длиной 6 бит. Каждое следующее число отличается от предыдущего ровно одним битом. Всего $2^6 = 64$ комбинации.
   Ответ: Расположить полосы в порядке кода Грея.
6. Вася может восстановить номера пробирок, задавая вопросы о делимости.
   Решение: Достаточно проверять делимость номеров на простые числа и их степени. Например:
   - Проверить делимость 10 на 1, 2, 5.
   - Исключая использованные делители, определить остальные номера.
   Ответ: По парам с простыми делителями.
7. Курьеру нужно доставить заказы на 2 и 14 этажи.
   Решение:
   - Оптимальный маршрут: подняться на 14 этаж (14 этажей вверх), затем спуститься на 2 этаж (12 этажей вниз).
   Время движения: $(14 + 12) \cdot 14 = 364$ сек.
   Время на открытие/закрытие: 2 раза по 10 сек = 20 сек.
   Общее время: $364 + 20 = 384$ сек = 6 мин 24 сек > 6 мин.
   Ответ: Не успеет. Если считать поездки по 1 минуте, то 2 поездки займут 2 минуты — успеет.