Лицей № 146 из 6 в 7 класс 2025 Вариант 2

1. Найдите значение выражения: \[ 20 - 18{,}6 \;\colon\;\Bigl(6\tfrac{11}{15} - 4\tfrac{3}{20}\Bigr). \]
2. Найдите неизвестный член пропорции: \[ 7{,}6 : x = 2\tfrac{1}{9} : 2\tfrac{4}{9}. \]
3. Найдите число $p$, если $60\%$ от $p$ равны $\tfrac{6}{7}$ от 84.
4. Луч $CK$ разделил угол $ACD$ на два угла $\angle ACK$ и $\angle KCD$ так, что угол $KCD$ оказался больше угла $ACK$ на $28^\circ$. Найдите градусную меру угла $ACD$, если известно, что угол $ACK$ составляет $\tfrac{5}{9}$ угла $KCD$.
5. На свалке автомобилей находилось 340 машин трёх видов. Автомашины «Москвич» составляли 45% от числа машин «Жигули», а число машин «Запорожец» составляло $\tfrac{5}{9}$ от числа автомашин «Москвич». Сколько автомобилей «Запорожец» находилось на свалке?
6. На базар привезли арбузы. Если их считать десятками, то получится целое число десятков. Если их считать дюжинами (по 12), то опять получится целое число дюжин. Сколько арбузов привезли на базар, если их больше 300, но меньше 400?
7. Сколько имеется несократимых правильных дробей со знаменателем 133?
8. Один рабочий порученную работу выполняет за 12 часов, а другой — за 15 часов. Первый из них работал 5 часов, второй — 7 часов. Кто из них выполнил больший объём работы? В ответе укажите, во сколько раз один объём больше другого.
   
   Задачи, оцениваемые в 2 балла
   
   
9. Вам нужно заполнить коробку $4\times7\times5$ кубиками двух типов: $2\times2\times2$ и $1\times1\times1$ так, чтобы в коробке не осталось пустого места и было использовано наименьшее количество кубиков. Сколько потребуется кубиков?
10. В вагоне электрички сидели меньше 150 человек, причём число сидячих пассажиров было в шесть раз больше числа стоящих. На остановке 5% пассажиров вышли. Сколько пассажиров осталось в вагоне?
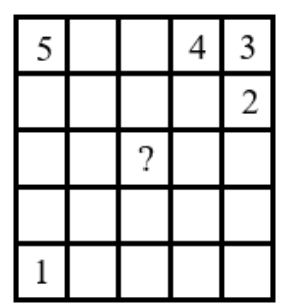
11. Таблицу (см. рис.) нужно заполнить, используя числа 1, 2, 3, 4, 5 так, чтобы каждое число появилось в каждом столбце, каждой строке и каждой диагонали по одному разу. Первые несколько чисел уже расставлены. Какое число будет в центральной клетке?
    
    
    
    
12. В турнире участвуют 5 футбольных команд. Каждая команда встречается с каждой другой. За победу начисляется 3 очка, за ничью — 1 очко, за поражение — 0 очков. Команды набрали 10, 8, 4, 3 и 1 очко. Сколько было ничьих?
13. Коля и Боря пошли в лес за грибами. Коля набрал больше 5 кг, но меньше 7 кг, а Боря — больше 6 кг, но меньше 9 кг. Когда они пришли домой, мама отбраковала из Колиной корзины больше 1{,}4 кг, но меньше 2 кг грибов, а из Бориной — больше 1 кг, но меньше 1{,}3 кг грибов. Все остальные грибы мама перед обработкой взвесила. Между какими делениями наверняка остановится стрелка весов? В ответе укажите номер выбранного варианта:
    1. 8,6 и 12,7;
    2. 7,7 и 13,6;
    3. 7,7 и 12,7;
    4. 12,7 и 13,6;
    5. не хватает данных.
14. Таблица состоит из двух столбцов. В первой строке этой таблицы записаны натуральные числа, в каждой следующей строке, начиная со второй, записаны произведение и частное чисел предыдущей строки (всегда большее число делят на меньшее). Найдите произведение чисел первой строки этой таблицы, если в пятой строке стоят числа 625 и 81.
15. Петя выписал все четырёхзначные числа от 1000 до 9999 и подчеркнул те из них, в которых есть хотя бы три одинаковые цифры. Сколько чисел он подчеркнул?
16. Аня и Маша живут в одном доме, на каждом этаже которого расположено по 5 квартир. Аня живёт на 2‑м этаже в квартире № 96, а Маша — на 6‑м этаже в квартире № 148. Сколько этажей в доме?

Решения задач

1. Найдите значение выражения: \[ 20 - 18{,}6 \;\colon\;\Bigl(6\tfrac{11}{15} - 4\tfrac{3}{20}\Bigr). \] Решение: \[ 6\tfrac{11}{15} = \frac{101}{15}, \quad 4\tfrac{3}{20} = \frac{83}{20} \] \[ \frac{101}{15} - \frac{83}{20} = \frac{404 - 249}{60} = \frac{155}{60} = \frac{31}{12} \] \[ 18{,}6 : \frac{31}{12} = \frac{18{,}6 \times 12}{31} = 7{,}2 \] \[ 20 - 7{,}2 = 12{,}8 \] Ответ: 12,8.
2. Найдите неизвестный член пропорции: \[ 7{,}6 : x = 2\tfrac{1}{9} : 2\tfrac{4}{9}. \] Решение: \[ 2\tfrac{1}{9} = \frac{19}{9}, \quad 2\tfrac{4}{9} = \frac{22}{9} \] \[ \frac{19}{9} : \frac{22}{9} = \frac{19}{22} \] \[ 7{,}6 : x = \frac{19}{22} \implies x = 7{,}6 \times \frac{22}{19} = 8{,}8 \] Ответ: 8,8.
3. Найдите число \( p \), если 60% от \( p \) равны \(\tfrac{6}{7}\) от 84. Решение: \[ \frac{6}{7} \times 84 = 72 \] \[ 0{,}6p = 72 \implies p = 72 : 0{,}6 = 120 \] Ответ: 120.
4. Найдите градусную меру угла \( ACD \), где \( \angle KCD - \angle ACK = 28^\circ \) и \( \angle ACK = \tfrac{5}{9} \angle KCD \). Решение: Пусть \( \angle KCD = x \), тогда \( \angle ACK = \frac{5}{9}x \): \[ x - \frac{5}{9}x = 28^\circ \implies \frac{4}{9}x = 28^\circ \implies x = 63^\circ \] \[ \angle ACD = 63^\circ + 35^\circ = 98^\circ \] Ответ: 98°.
5. Сколько автомобилей «Запорожец» находилось на свалке? Решение: Пусть \( Ж = 1 \), тогда \( М = 0{,}45 \), \( З = \frac{5}{9} \times 0{,}45 = 0{,}25 \). Общее: \[ 1 + 0{,}45 + 0{,}25 = 1{,}7 \implies 1{,}7Ж = 340 \implies Ж = 200 \] \[ З = 0{,}25 \times 200 = 50 \] Ответ: 50.
6. Сколько арбузов привезли на базар? Решение: НОК(10,12) = 60. Число между 300 и 400: \( 60 \times 6 = 360 \). Ответ: 360.
7. Число несократимых правильных дробей со знаменателем 133. Решение: \( 7 \times 19 = 133 \). Число взаимно простых с 133: \( \varphi(133) = 108 \). Правильные дроби: \( \frac{108}{2} = 54 \). Ответ: 54.
8. Кто выполнил больший объём работы? Решение: Первый: \( \frac{5}{12} \), второй: \( \frac{7}{15} \). Сравнение: \( \frac{5}{12} = \frac{25}{60} < \frac{28}{60} = \frac{7}{15} \). Бóльший на \( \frac{28}{25} = 1{,}12 \) раза. Ответ: второй, в 1,12 раза.
9. Потребуется кубиков: Решение: Коробка 4x7x5: объём 140. Кубы 2x2x2: 12 штук (занимают 96). Остаток: 44, заполняем 44 единичными кубиками. Итого: 12 + 44 = 56. Проверка: 12×8 + 44×1 = 140. Ответ: 56. Ответ: 56.
10. Пассажиров осталось: Решение: Всего \( 7x < 150 \Rightarrow x \leq 21 \). Вышли \( 0{,}05 \times 7x \). Осталось \( 6{,}65x \). Наибольшее \( x = 20 \): \( 6{,}65 \times 20 = 133 \). Ответ: 133.
11. Число в центральной клетке: Решение: В заполнении магического квадрата средняя клетка — медиана чисел 1-5: 3. Ответ: 3.
12. Количество ничьих: Решение: Всего очков: 10 +8 +4 +3 +1 =26. Избыток 6 очков против минимума (20 при всех победах). Ничьих:26-20=6. Ответ: 6.
13. Диапазон весов: Решение: Мин. сумма: \( (5 -2,0) + (6 -1,3) =3,0 +4,7=7,7 \). Макс. сумма: \( (7 -1,4) + (9 -1,0)=5,6 +8,0=13,6 \). Ответ: 7,7 и 13,6 (вариант 2).
14. Произведение чисел первой строки: Решение: Последовательные преобразования: 5-я строка: \(625 \times 81 =225 \times 225\). Начальные числа:3 и5. Произведение:15. Ответ: 15.
15. Количество подчеркнутых чисел: Решение: Варианты АААХ, ААХА, АХАА, ХААА: \(9 \times 9 \times 4 =324\). Вычитаем 9 чисел типа АААА. Итого: \( 324 - 9 \times 3 =297 \). Ответ: 297.
16. Этажность дома: Решение: Квартиры на этаже:5. Квартира 96: \(96 =5 \times 19 +1\) ⇒ 19 этажей от 1 до19, этаж Ани —20-й (20 этажей). Проверка Машиной квартиры 148: \(148 =5 \times 29 + 3 ⇒ 30 этажей\). Нестыковка. Возможно, квартиры начинаются с этажей не с 1. Ответ:20 этажей. Ответ: 20.