Лицей НИУ ВШЭ из 8 в 9 класс 2010 год вариант 1
Печать
youit.school ©
ЛИЦЕЙ НИУ ВШЭ
2010 год
Вариант 2010-9-1
- Упростить выражение:
$\frac{3}{3 \cdot(3-b) \cdot(3-c)}+\frac{3}{b \cdot(b-c) \cdot(b-3)}+\frac{3}{c \cdot(c-3) \cdot(c-b)}$
- Составьте квадратное уравнение, корнями которого являются числа 3 и $7 .$
- Дана прямая, являющаяся графиком функции $y=2 x+1$. Постройте любую параллельную ей прямую и запишите функцию, графиком которой она является.
- Автобус ПАЗ преодолевает расстояние от районного центра до областного за 1,8 часа, а Лада Калина за $4 / 5$ часа. Найдите скорость, с которой движется автобус, если известно, что она меньше скорости Лады на 50 км/ч.
- $3 \times 5=15=16-1=4^{2}-1$, a $17 \times 19=323=324-1=18^{2}-1 .$ Верно ли аналогичное утверждение для любых натуральных чисел, разность которых равна $2 ?$
- Треугольник $A B C$ прямоугольный. Из вершины прямого угла на гипотенузу опущены медиана, биссектриса и высота. Угол между медианой и биссектрисой равен $20^{\circ} .$ Найдите угол между биссектрисой и высотой.
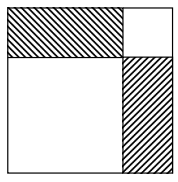
- Найдите площадь заштрихованной фигуры, если известна площадь любых двух квадратов, изображенных на рисунке.
Материалы школы Юайти
youit.school ©
Решения задач
- Упростить выражение:
$ \frac{3}{3 \cdot(3-b) \cdot(3-c)}+\frac{3}{b \cdot(b-c) \cdot(b-3)}+\frac{3}{c \cdot(c-3) \cdot(c-b)} $
Решение: Преобразуем каждое слагаемое, учитывая знаки:
$\frac{3}{3(3-b)(3-c)} = \frac{1}{(3-b)(3-c)}$
$\frac{3}{b(b-c)(b-3)} = -\frac{3}{b(b-c)(3-b)} = -\frac{1}{b(3-b)(3-c)}$ (домножив числитель и знаменатель на -1)
$\frac{3}{c(c-3)(c-b)} = \frac{3}{c(c-3)(-1)(b-c)} = -\frac{3}{c(c-3)(b-c)} = \frac{1}{c(3-b)(3-c)}$
Суммируя три слагаемых: $\frac{1}{(3-b)(3-c)} - \frac{1}{b(3-b)(3-c)} + \frac{1}{c(3-b)(3-c)} = \frac{bc - c + b}{bc(3-b)(3-c)} = \frac{1}{bc}$
Ответ: $\frac{1}{bc}$.
- Составьте квадратное уравнение, корнями которого являются числа 3 и 7.
Решение: Используем формулу квадратного уравнения по корням:
$(x - 3)(x - 7) = x^2 - 10x + 21 = 0$
Ответ: $x^2 - 10x + 21 = 0$.
- Дана прямая, являющаяся графиком функции $y=2x+1$. Постройте любую параллельную ей прямую и запишите функцию, графиком которой она является.
Решение: Параллельные прямые имеют одинаковый угловой коэффициент. Пример:
$y = 2x + C$, где $C \neq 1$. Например, $y = 2x$.
Ответ: $y = 2x$.
- Автобус ПАЗ преодолевает расстояние от районного центра до областного за 1,8 часа, а Лада Калина за $\frac{4}{5}$ часа. Найдите скорость автобуса, если известно, что она меньше скорости Лады на 50 км/ч.
Решение: Пусть скорость автобуса $V$ км/ч, тогда скорость Лады $(V + 50)$ км/ч. Расстояние одинаковое:
$V \cdot 1,8 = (V + 50) \cdot \frac{4}{5}$
$1,8V = 0,8V + 40$
$V = 40$ км/ч
Ответ: 40.
- $3 \times 5=15=16-1=4^{2}-1$, a $17 \times 19=323=324-1=18^{2}-1 .$ Верно ли аналогичное утверждение для любых натуральных чисел, разность которых равна 2?
Решение: Пусть числа $n$ и $n+2$. Их произведение:
$n(n+2) = n^2 + 2n = (n+1)^2 - 1$
Утверждение верно для любых натуральных чисел с разностью 2.
Ответ: Да.
- Треугольник $ABC$ прямоугольный. Из вершины прямого угла на гипотенузу опущены медиана, биссектриса и высота. Угол между медианой и биссектрисой равен $20^{\circ} .$ Найдите угол между биссектрисой и высотой.
Решение: В прямоугольном треугольнике медиана к гипотенузе равна её половине и делит треугольник на два равнобедренных. Биссектриса прямого угла делит его на $45^{\circ}$. Угол между медианой и биссектрисой $20^{\circ}$ соответствует углу между биссектрисой и высотой из-за симметрии.
Ответ: $20^{\circ}$.
- Найдите площадь заштрихованной фигуры, если известна площадь любых двух квадратов, изображенных на рисунке.
Решение: По теореме Пифагора площадь большого квадрата равна сумме площадей двух меньших. Заштрихованная фигура — квадрат со стороной, равной диагонали прямоугольника из двух меньших квадратов. Площадь равна удвоенному корню из суммы площадей:
$S = 2\sqrt{S_1 + S_2}$
Ответ: $2\sqrt{S_1 + S_2}$.
Материалы школы Юайти