Лицей КФУ из 8 в 9 класс 2023 год вариант 2

ЛИЦЕЙ КФУ

2023 год

Вариант 2

1. Вычислите: \[ \sqrt{19 - 8\sqrt{3}} \;+\; \sqrt{11 - 4\sqrt{7}} \;-\; \sqrt{10 - 2\sqrt{21}}. \]
2. Упростите выражение и найдите его значение при \(a = -3\sqrt{3}\): \[ \biggl(\frac{1}{\,a - \sqrt{3}\,} \;-\; \frac{a^2 + 6}{\,a^3 - 3\sqrt{3}\,}\biggr) \;\cdot\; \biggl(\frac{a + \sqrt{3}}{3} + \frac{1}{a}\biggr). \]
3. Решите уравнение, сделав соответствующую замену переменной: \[ \frac{12|x| - 3x^2}{\,x^2 - 4|x| + 1\,} = x^2 - 4|x|. \]
4. Найдите множество отрицательных решений системы неравенств: \[ \begin{cases} 12x^2 - (3x + 4)(4x - 1) < 8,\\[0.5ex] \displaystyle \frac{x - 2}{4} - x < 3(2 - x). \end{cases} \]
5. За 16 дней двумя экскаваторами можно вырыть \(\tfrac{4}{9}\) траншеи для прокладки труб. За сколько дней выполнил бы эту работу каждый экскаватор, если одному из них для этого понадобилось бы на 30 дней больше, чем другому?
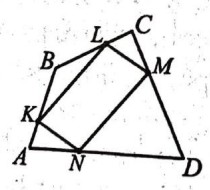
6. На сторонах четырёхугольника \(ABCD\) взяты точки \(K,L,M,N\) так, что \[ \frac{AK}{BK} \;=\; \frac{AN}{DN} \;=\; \frac{CL}{BL} \;=\; \frac{CM}{DM} \;=\;\tfrac{5}{7}. \] (см. рис.) Найдите площадь четырёхугольника \(KLMN\), если площадь \(ABCD\) равна 72.
   

Решения задач

1. Вычислите: \[ \sqrt{19 - 8\sqrt{3}} \;+\; \sqrt{11 - 4\sqrt{7}} \;-\; \sqrt{10 - 2\sqrt{21}}. \]
   Решение: Представим каждое подкоренное выражение в виде квадрата разности: \(\sqrt{19 - 8\sqrt{3}} = \sqrt{(4 - \sqrt{3})^2} = 4 - \sqrt{3}\) \(\sqrt{11 - 4\sqrt{7}} = \sqrt{(\sqrt{7} - 2)^2} = \sqrt{7} - 2\) \(\sqrt{10 - 2\sqrt{21}} = \sqrt{(\sqrt{7} - \sqrt{3})^2} = \sqrt{7} - \sqrt{3}\) Подставим упрощенные выражения в исходное выражение: \[ (4 - \sqrt{3}) + (\sqrt{7} - 2) - (\sqrt{7} - \sqrt{3}) = 4 - \sqrt{3} + \sqrt{7} - 2 - \sqrt{7} + \sqrt{3} = 2 \] Ответ: \(2\).
2. Упростите выражение и найдите его значение при \(a = -3\sqrt{3}\): \[ \biggl(\frac{1}{\,a - \sqrt{3}\,} \;-\; \frac{a^2 + 6}{\,a^3 - 3\sqrt{3}\,}\biggr) \;\cdot\; \biggl(\frac{a + \sqrt{3}}{3} + \frac{1}{a}\biggr). \]
   Решение: Упростим первую часть выражения: \[ \frac{1}{a - \sqrt{3}} - \frac{a^2 + 6}{(a - \sqrt{3})(a^2 + a\sqrt{3} + 3)} = \frac{a^2 + a\sqrt{3} + 3 - (a^2 + 6)}{(a - \sqrt{3})(a^2 + a\sqrt{3} + 3)} = \frac{a\sqrt{3} - 3}{(a - \sqrt{3})(a^2 + a\sqrt{3} + 3)} \] Упростим вторую часть выражения: \[ \frac{a + \sqrt{3}}{3} + \frac{1}{a} = \frac{a^2 + a\sqrt{3} + 3}{3a} \] Перемножим упрощенные части: \[ \frac{a\sqrt{3} - 3}{(a - \sqrt{3})(a^2 + a\sqrt{3} + 3)} \cdot \frac{a^2 + a\sqrt{3} + 3}{3a} = \frac{\sqrt{3}(a - \sqrt{3})}{(a - \sqrt{3})} \cdot \frac{1}{3a} = \frac{\sqrt{3}}{3a} \] Подставим \(a = -3\sqrt{3}\): \[ \frac{\sqrt{3}}{3 \cdot (-3\sqrt{3})} = -\frac{1}{9} \] Ответ: \(-\dfrac{1}{9}\).
3. Решите уравнение: \[ \frac{12|x| - 3x^2}{\,x^2 - 4|x| + 1\,} = x^2 - 4|x|. \]
   Решение: Сделаем замену \( t = |x| \geq 0 \). Уравнение примет вид: \[ \frac{12t - 3t^2}{t^2 - 4t + 1} = t^2 - 4t \] Перенесем влево: \[ \frac{12t - 3t^2 - (t^2 - 4t)(t^2 - 4t + 1)}{t^2 - 4t + 1} = 0 \] Раскроем скобки в числителе: \[ -t^4 + 8t^3 - 20t^2 + 16t = 0 \quad \Rightarrow \quad t(t^3 - 8t^2 + 20t - 16) = 0 \] Корни: \( t = 0 \), \( t = 2 \) (двойной), \( t = 4 \). Возвращаясь к исходной переменной \( x \): \[ |x| = 0 \Rightarrow x = 0; \quad |x| = 2 \Rightarrow x = \pm 2; \quad |x| = 4 \Rightarrow x = \pm 4 \] Ответ: \( 0 \); \( \pm 2 \); \( \pm 4 \).
4. Найдите множество отрицательных решений системы неравенств: \[ \begin{cases} 12x^2 - (3x + 4)(4x - 1) < 8,\\[0.5ex] \displaystyle \frac{x - 2}{4} - x < 3(2 - x). \end{cases} \]
   Решение: Первое неравенство: \[ 12x^2 - 12x^2 -13x +4 < 8 \quad \Rightarrow \quad -13x -\dfrac{4}{13} \] Второе неравенство: \[ -\dfrac{3x}{4} - 0.5 < 6 -3x \quad \Rightarrow \quad 2.25x < 6.5 \quad \Rightarrow \quad x < \dfrac{26}{9} \] Пересечение с отрицательными значениями \( x \): \[ x \in \left( -\dfrac{4}{13}; \, 0 \right) \] Ответ: \( \left( -\dfrac{4}{13}; \, 0 \right) \).
5. За 16 дней двумя экскаваторами можно вырыть \(\tfrac{4}{9}\) траншеи. Понадобится на 30 дней больше одному экскаватору, чем другому. Найти время работы каждого.
   Решение: Пусть первый экскаватор выполняет работу за \( x \) дней, второй — за \( x + 30 \). Совместная производительность: \[ \dfrac{1}{x} + \dfrac{1}{x + 30} = \dfrac{1}{36} \] Решение уравнения: \[ x^2 -42x -1080 = 0 \quad \Rightarrow \quad x = 60 \quad (x > 0) \] Ответ: первый — 60 дней, второй — 90 дней.
6. Найдите площадь четырёхугольника \(KLMN\), если площадь \(ABCD\) равна 72, а точки делят стороны в отношении \(\tfrac{5}{7}\).
   Решение: Коэффициент деления сторон: \(\tfrac{5}{12}\) и \(\tfrac{7}{12}\). Площадь четырёхугольника \(KLMN\) вычисляется по формуле: \[ S_{KLMN} = S_{ABCD} \cdot \left( 1 - 4 \cdot \dfrac{5 \cdot 7}{(5 + 7)^2} \right) = 72 \cdot \dfrac{5}{12} = 30 \] Ответ: \(30\).