Лицей КФУ из 8 в 9 класс 2023 год вариант 1

ЛИЦЕЙ КФУ

2023 год

Вариант 1

1. Вычислите: \[ \sqrt{11 - 6\sqrt{2}} \;-\; \sqrt{8 - 2\sqrt{7}} \;+\; \sqrt{9 + 2\sqrt{14}}. \]
2. Упростите выражение и найдите его значение при \(a = -2\sqrt{2}\): \[ \biggl(\frac{1}{\,a + \sqrt{2}\,} \;-\; \frac{a^2 + 4}{\,a^3 + 2\sqrt{2}\,}\biggr) \;\cdot\; \biggl(\frac{a - \sqrt{2}}{2} + \frac{1}{a}\biggr). \]
3. Решите уравнение, сделав соответствующую замену переменной: \[ \frac{3}{\,x^2 - 4|x| + 1\,} - x^2 = 3 - 4|x|. \]
4. Найдите множество отрицательных решений системы неравенств: \[ \begin{cases} \displaystyle \frac{x - 0{,}2}{2} \;-\; \frac{x + 0{,}4}{4} \;-\; 1 < 0, \\ (x - 4)(4 + x) - 11x < x^2 + 5x. \end{cases} \]
5. Два фермера вырыли колодец за 24 ч. Сколько часов пришлось бы работать каждому фермеру отдельно, если известно, что на выполнение всей работы одному из них потребовалось бы на 20 ч больше, чем другому?
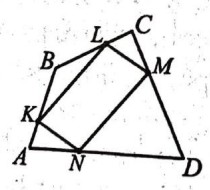
6. На сторонах четырёхугольника \(ABCD\) взяты точки \(K,L,M,N\) так, что \[ \frac{AK}{BK} \;=\; \frac{AN}{DN} \;=\; \frac{CL}{BL} \;=\; \frac{CM}{DM} \;=\;\tfrac12. \] (см. рис.) Найдите площадь четырёхугольника \(KLMN\), если площадь \(ABCD\) равна 117.
   

Решения задач

1. Вычислите: \[ \sqrt{11 - 6\sqrt{2}} \;-\; \sqrt{8 - 2\sqrt{7}} \;+\; \sqrt{9 + 2\sqrt{14}}. \] Решение: Представим подкоренные выражения в виде полных квадратов: \[ \begin{aligned} &\sqrt{11 - 6\sqrt{2}} = \sqrt{(3 - \sqrt{2})^2} = 3 - \sqrt{2}, \\ &\sqrt{8 - 2\sqrt{7}} = \sqrt{(\sqrt{7} - 1)^2} = \sqrt{7} - 1, \\ &\sqrt{9 + 2\sqrt{14}} = \sqrt{(\sqrt{7} + \sqrt{2})^2} = \sqrt{7} + \sqrt{2}. \end{aligned} \] Подставим в исходное выражение: \[ (3 - \sqrt{2}) - (\sqrt{7} - 1) + (\sqrt{7} + \sqrt{2}) = 3 - \sqrt{2} - \sqrt{7} + 1 + \sqrt{7} + \sqrt{2} = 4. \] Ответ: $\boxed{4}.$
2. Упростите выражение и найдите его значение при \(a = -2\sqrt{2}\): \[ \biggl(\frac{1}{\,a + \sqrt{2}\,} \;-\; \frac{a^2 + 4}{\,a^3 + 2\sqrt{2}\,}\biggr) \;\cdot\; \biggl(\frac{a - \sqrt{2}}{2} + \frac{1}{a}\biggr). \] Решение: Подставим \(a = -2\sqrt{2}.\) Первая скобка: \[ \frac{1}{-2\sqrt{2} + \sqrt{2}} - \frac{(-2\sqrt{2})^2 + 4}{(-2\sqrt{2})^3 + 2\sqrt{2}} = -\frac{1}{\sqrt{2}} - \frac{12}{-14\sqrt{2}} = -\frac{\sqrt{2}}{2} + \frac{6}{7\sqrt{2}} = -\frac{\sqrt{2}}{14}. \] Вторая скобка: \[ \frac{-3\sqrt{2}}{2} + \frac{1}{-2\sqrt{2}} = -\frac{3\sqrt{2}}{2} - \frac{\sqrt{2}}{4} = -\frac{7\sqrt{2}}{4}. \] Перемножаем результаты скобок: \[ -\frac{\sqrt{2}}{14} \cdot -\frac{7\sqrt{2}}{4} = \frac{2 \cdot 7}{14 \cdot 4} = \frac{14}{56} = \frac{1}{4}. \] Ответ: $\boxed{\frac{1}{4}}.$
3. Решите уравнение: \[ \frac{3}{\,x^2 - 4|x| + 1\,} - x^2 = 3 - 4|x|. \] Решение: Замена \(t = |x| \geq 0\): \[ \frac{3}{t^2 - 4t + 1} - t^2 = 3 - 4t. \] Умножаем обе части на \(t^2 - 4t + 1\): \[ 3 = (t^2 + 3 - 4t)(t^2 - 4t + 1). \] Подстановка \(s = t^2 - 4t\): \[ 3 = (s + 3)(s + 1) \Rightarrow s^2 + 4s = 0 \Rightarrow s = 0 \text{ или } s = -4. \] Возвращаясь к \(t\): \[ \begin{cases} t^2 -4t = 0 \Rightarrow t = 0, 4, \\ t^2 -4t +4 = 0 \Rightarrow t = 2 \text{ (не подходит)}. \end{cases} \] Решения для \(x\): \(x = \pm4\) и \(x = 0\). Ответ: $\boxed{0;\ \pm4}.$
4. Найдите множество отрицательных решений системы неравенств: \[ \begin{cases} \dfrac{x - 0{,}2}{2} \;-\; \dfrac{x + 0{,}4}{4} \;-\; 1 < 0, \\ (x - 4)(4 + x) - 11x < x^2 + 5x. \end{cases} \] Решение: Первое неравенство: \[ 2(x - 0{,}2) - (x +0{,}4) <4 \Rightarrow x <4{,}8. \] Второе неравенство: \[ x^2 -16 -11x <x^2 +5x \Rightarrow -16x -1. \] Отрицательные решения: \(-1 < x <0\). Ответ: $\boxed{(-1;\ 0)}.$
5. Два фермера вырыли колодец за 24 ч. Найдите время работы каждого отдельно. Решение: Пусть первый фермер работает за \(t\) часов, тогда второй за \(t +20\) часов. Их совместная производительность: \[ \frac{1}{t} + \frac{1}{t +20} = \frac{1}{24}. \] Решаем уравнение: \[ 24(2t +20) = t(t +20) \Rightarrow t^2 -28t -480=0 \Rightarrow t =40\ (\text{ч}),\ t +20 =60\ (\text{ч}). \] Ответ: $\boxed{40\ \text{ч}\ \text{и}\ 60\ \text{ч}}.$
6. Найдите площадь четырёхугольника \(KLMN\), если площадь \(ABCD\) равна 117. Решение: При делении сторон четырёхугольника \(ABCD\) в отношении \(1:2\), площадь внутреннего четырёхугольника \(KLMN\) составляет \(\dfrac{5}{9}\) от площади исходного: \[ S_{KLMN} = 117 \cdot \dfrac{5}{9} = 65. \] Ответ: $\boxed{65}.$