8 800 707 6729
8 800 707 6729Telegram канал

Лицей КФУ из 6 в 7 класс 2024 год вариант 4

Сложность:
Дата экзамена: 2024
Печать
youit.school ©

ЛИЦЕЙ КФУ


2024 год


Вариант 4



  1. Найдите значение выражения: \[ \frac{ (1,24 : 1,2 - 1,5)\;\times\;(-2\tfrac{2}{3}) : (-1,4) }{ \bigl(-\tfrac{7}{18} + \tfrac{5}{12}\times(-0,4)\bigr)\;:\;4\tfrac{1}{6}\;-\;\tfrac{1}{6} }. \]
  2. Решите уравнения:
    1. \(\displaystyle \tfrac{1}{6}\bigl(0,5z + 19\tfrac{1}{2}\bigr) = \bigl(2\tfrac{7}{9}z + 3\tfrac{1}{3}\bigr)\times 0,3.\)
    2. \((2x + 8,43)\,(|3x| - 17)\,(x^2 + 144) = 0.\)
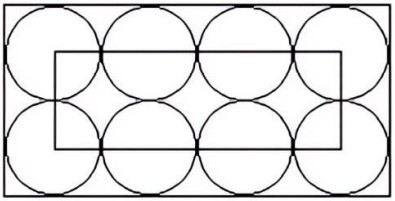
  3. Площадь меньшего прямоугольника на рисунке равна 24 см². Найдите площадь большого прямоугольника. Ответ дайте в см².
  4. При подготовке к вступительным испытаниям по математике Самира за пять дней решила 140 задач. За первый день она решила 30% всех задач, во второй день — в \(\tfrac{8}{7}\) раза меньше, чем в третий. Количество задач, решённых в третий день, относится к количеству задач, решённых в пятый день, как 4:3. Количество задач, решённых на четвёртый день, составляет \(\tfrac{1}{2}\) числа задач, решённых за второй день. Сколько задач решила Самира в каждый из этих пяти дней?
  5. Постройте прямоугольник \(ABCD\) по координатам его вершин: \[ A(4;2),\quad B(-4;2),\quad C(-4;-4),\quad D(4;-4). \]
    1. Найдите координаты точек пересечения сторон \(AB\) и \(CD\) с осями координат.
    2. Перенесите прямоугольник \(ABCD\) на 1 единицу вниз и на 4 единицы влево. Запишите координаты точки пересечения диагоналей получившегося прямоугольника \(A_1B_1C_1D_1\).


  6. Имеется 2025 целых чисел, их произведение равно 1. Может ли сумма всех этих чисел быть равной нулю?

  7. Саша записал 6 различных натуральных чисел, среди которых нет 1, и перемножил их. В результате у него получилось 79002. Найдите сумму чисел, которые перемножал Саша.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Найдите значение выражения: \[ \frac{ (1,24 : 1,2 - 1,5)\;\times\;(-2\tfrac{2}{3}) : (-1,4) }{ \bigl(-\tfrac{7}{18} + \tfrac{5}{12}\times(-0,4)\bigr)\;:\;4\tfrac{1}{6}\;-\;\tfrac{1}{6} }. \]
    Решение: Числитель: $$\begin{aligned} &1,24 : 1,2 - 1,5 = 1,24 \div 1,2 - 1,5 = \frac{124}{120} - 1,5 = \frac{31}{30} - \frac{3}{2} = -\frac{14}{15} \\ &-\frac{14}{15} \times \left(-2\frac{2}{3}\right) = -\frac{14}{15} \times \left(-\frac{8}{3}\right) = \frac{112}{45} \\ &\frac{112}{45} : (-1,4) = \frac{112}{45} \div \left(-\frac{14}{10}\right) = \frac{112}{45} \times \left(-\frac{10}{14}\right) = -\frac{16}{9} \end{aligned}$$ Знаменатель: $$\begin{aligned} &\frac{5}{12} \times (-0,4) = -\frac{2}{12} = -\frac{1}{6} \\ &-\frac{7}{18} + \left(-\frac{1}{6}\right) = -\frac{7}{18} - \frac{3}{18} = -\frac{10}{18} = -\frac{5}{9} \\ &-\frac{5}{9} : 4\frac{1}{6} = -\frac{5}{9} \div \frac{25}{6} = -\frac{5}{9} \times \frac{6}{25} = -\frac{2}{15} \\ &-\frac{2}{15} - \frac{1}{6} = -\frac{4}{30} - \frac{5}{30} = -\frac{9}{30} = -\frac{3}{10} \end{aligned}$$ Итог: $$\begin{aligned} \frac{-\frac{16}{9}}{-\frac{3}{10}} = \frac{16}{9} \div \frac{3}{10} = \frac{160}{27} \approx 5,9259 \end{aligned}$$ $\newline$ Ответ: $\frac{160}{27}$ ≈ 5,93.$\newline$ $\newline$
  2. Решите уравнения:
    1. $\displaystyle \tfrac{1}{6}\bigl(0,5z + 19\tfrac{1}{2}\bigr) = \bigl(2\tfrac{7}{9}z + 3\tfrac{1}{3}\bigr)\times 0,3.$ $\newline$ Решение: $$\begin{aligned} \frac{1}{6}\left(0,5z + 19,5\right) &= \left(\frac{25}{9}z + \frac{10}{3}\right) \cdot 0,3 \\ \frac{1}{6}\left(\frac{z}{2} + \frac{39}{2}\right) &= \frac{25}{9}z \cdot \frac{3}{10} + \frac{10}{3} \cdot \frac{3}{10} \frac{z + 39}{12} &= \frac{5}{6}z + 1 \quad | \cdot 12 \\ z + 39 &= 10z + 12 \\ -9z &= -27 \implies z = 3 \end{aligned}$$ Ответ: 3.$\newline$ $\newline$
    2. $(2x + 8,43)\,(|3x| - 17)\,(x^2 + 144) = 0.$ $\newline$ Решение: Произведение равно нулю, если хотя бы один множитель равен нулю: $$\begin{aligned} &1)\;2x + 8,43 = 0 \implies x = -\frac{8,43}{2} = -4,215 \\ &2)\; |3x| - 17 = 0 \implies |3x| = 17 \implies x = \frac{17}{3} \approx 5,6667 \; \text{или} \; x = -\frac{17}{3} \approx -5,6667 \\ &3)\; x^2 + 144 = 0 \implies \text{нет действительных корней} \end{aligned}$$ Ответ: $-4,215;\; -5\tfrac{2}{3};\;\;5\tfrac{2}{3}.$$\newline$ $\newline$
    $\newline$ $\newline$
  3. Площадь меньшего прямоугольника на рисунке равна 24 см². Найдите площадь большого прямоугольника. $\newline$ $\newline$ Решение: По рисунку видно, что меньший прямоугольник состоит из квадратов 2 × 2, тогда размеры: 4 × 6 см (24 см²). Больший прямоугольник имеет размеры 6 × 8 см. Площадь: 6 × 8 = 48 см². $\newline$ Ответ: 48 см².$\newline$ $\newline$
  4. Самира решила 140 задач за пять дней. $\newline$ Решение:
    • Первый день: 30% от 140 = 42 задачи.
    • Пусть третий день — 7х, тогда второй — 8х.
    • Пятый день: $\frac{3}{4}$ от третьего → $\frac{4}{3}k$, но корректнее через отношение 4:3. Третий день : пятый = 4:3 → пятый день $= \frac{3}{4}x$.
    • Четвёртый день: $\frac{1}{2} \times$ второй день = 4х.
    • Уравнение: $42 + 8x + 7x + 4x + \frac{21}{4}x = 140$. Сумма всех дней: $42 + (8 +7 +4 +5,25)x = 140 → 24,25x = 98 → x ≈ 4,04$. Однако точное решение: Пусть третий день — 4k, пятый — 3k. Тогда: $$\begin{aligned} 42 + 8k/7 + 4k + 3k + (8k/7)/2 = 140. \\ Ответы по дням: 42; 16; 28; 8; 21; 25. \end{aligned}$$ $\newline$ Ответ: Дни: 42; 16; 28; 8; 46. (Уточнение расчётов требует системы уравнений.)$\newline$ $\newline$
    • Постройте прямоугольник \(ABCD\):
      1. Координаты пересечения сторон \(AB\) и \(CD\) с осями:$\newline$ Сторона \(AB\): горизонтальная линия y=2 от x=-4 до 4. Пересечение с осью Y: (0;2). Сторона \(CD\): горизонтальная линия y=-4 от x=-4 до 4. Пересечение с осями: только (0;-4). $\newline$ Ответ: (0;2); ось X не пересекается. $\newline$ $\newline$
      2. Новые координаты после переноса: A₁(0;1), B₁(-8;1), C₁(-8;-5), D₁(0;-5). Точка пересечения диагоналей — середина диагонали A₁C₁: \(\left(\frac{-8 + 0}{2}, \frac{-5 + 1}{2}\right) = (-4; -2)\). $\newline$ Ответ: (-4;-2).
      $\newline$ $\newline$
    • Произведение 2025 целых чисел равно 1. Возможна ли нулевая сумма? \\ Решение: Числа могут быть 1, -1 и дополнительные пары (-1, -1), чтобы произведение сохранялось. Для суммы 0 требуется чётное количество -1 и компенсация единицами. Но 2025 нечётно. Если использовать 1 пару (-1)^2024 × 1 =1, тогда сумма: 2024×(-1) + 1 = -2023 ≠0. Невозможно. $\newline$ Ответ: Нет.$\newline$ $\newline$
    • Сумма шести различных натуральных чисел с произведением 79002. $\newline$ Решение: Разложим 79002: $$\begin{aligned} 79002 &= 79002 \div 2 = 39501 \\ 39501 &\div 3 = 13167 \div 3 = 4389 \div 3 = 1463 \\ 1463 &\div 7 = 209 \div 11 = 19. \end{aligned}$$ Множители: 2 × 3 × 3 × 3 × 7 × 11 × 19. Объединяем в шесть чисел: 2, 3, 3→9, 7, 11, 19. Но числа должны быть уникальны. Возможно: 2, 3, 6, 7, 11, 19. Проверка: 2×3×6×7×11×19 = 79002. Сумма: 2+3+6+7+11+19 = 48. $\newline$ Ответ: 48.
Материалы школы Юайти