Лицей КФУ из 6 в 7 класс 2024 год вариант 2

ЛИЦЕЙ КФУ

2024 год

Вариант 2

1. Найдите значение выражения: \[ \frac{ (1,68 : 1,6 - 1,3)\;\times\;(-2\tfrac{2}{9}) : (-1,8) }{ \bigl(-\tfrac{7}{16} + \tfrac{5}{14}\times(-0,7)\bigr)\;:\;4\tfrac{1}{8}\;-\;\tfrac{1}{4} }. \]
2. Решите уравнения:
   1. \(\displaystyle \tfrac{2}{3}\bigl(0,5z + 19\tfrac{1}{2}\bigr) = \bigl(2\tfrac{7}{9}z + 3\tfrac{1}{3}\bigr)\times 1,2.\)
   2. \((x^2 + 100)\,(4x + 5,36)\,(|5x| - 12) = 0.\)
3. Площадь меньшего прямоугольника на рисунке равна 96 см². Найдите площадь большого прямоугольника. Ответ дайте в см².
   
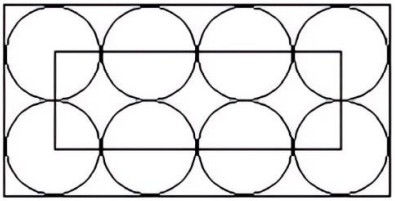
4. При подготовке к вступительным испытаниям по математике Руслан за пять дней решил 150 задач. За первый день он решил 24% всех задач, во второй день — в полтора раза меньше, чем в третий. Количество задач, решённых в третий день, относится к количеству задач, решённых в пятый день, как 4:5. Количество задач, решённых на четвёртый день, составляет \(\tfrac{5}{8}\) числа задач, решённых за второй день. Сколько задач решил Руслан в каждый из этих пяти дней?
5. Постройте прямоугольник \(ABCD\) по координатам его вершин: \[ A(3;4),\; B(-3;4),\; C(-3;-2),\; D(3;-2). \]
   1. Найдите координаты точек пересечения сторон \(AB\) и \(CD\) с осями координат.
   2. Перенесите прямоугольник \(ABCD\) на 1 единицу вниз и на 4 единицы влево. Запишите координаты точки пересечения диагоналей получившегося прямоугольника \(A_1B_1C_1D_1\).
   
   
   
6. Имеется 2023 целых числа, их произведение равно 1. Может ли сумма всех этих чисел быть равной нулю?
   
   
7. Никита записал 6 различных натуральных чисел, среди которых нет 1, и перемножил их. В результате у него получилось 54054. Найдите сумму чисел, которые перемножал Никита.

Решения задач

1. Найдите значение выражения: \[ \frac{ (1,68 : 1,6 - 1,3)\;\times\;(-2\tfrac{2}{9}) : (-1,8) }{ \bigl(-\tfrac{7}{16} + \tfrac{5}{14}\times(-0,7)\bigr)\;:\;4\tfrac{1}{8}\;-\;\tfrac{1}{4} }. \] Решение:
   Рассмотрим числитель: \[ \left(1{,}68 : 1{,}6 - 1{,}3\right) \cdot \left(-2\tfrac{2}{9}\right) : (-1{,}8) = \left(1{,}05 - 1{,}3\right) \cdot \left(-\tfrac{20}{9}\right) : \left(-\tfrac{9}{5}\right) = \] \[ (-0{,}25) \cdot \left(-\tfrac{20}{9}\right) : \left(-\tfrac{9}{5}\right) = \tfrac{5}{9} : \left(-\tfrac{9}{5}\right) = -\tfrac{25}{81}. \]
   Знаменатель: \[ \left(-\tfrac{7}{16} + \tfrac{5}{14} \cdot (-0{,}7)\right) : 4\tfrac{1}{8} - \tfrac{1}{4} = \left(-\tfrac{7}{16} - \tfrac{1}{4}\right) : \tfrac{33}{8} - \tfrac{1}{4} = \] \[ \left(-\tfrac{11}{16}\right) : \tfrac{33}{8} - \tfrac{1}{4} = -\tfrac{1}{6} - \tfrac{1}{4} = -\tfrac{5}{12}. \]
   Итоговое значение: \[ \frac{-\tfrac{25}{81}}{-\tfrac{5}{12}} = \tfrac{25}{81} \cdot \tfrac{12}{5} = \tfrac{60}{81} = \tfrac{20}{27} \approx 0{,}7407. \]
   Ответ: \(\boxed{\tfrac{20}{27}}\).
   
2. Решите уравнения:
   1. \(\displaystyle \tfrac{2}{3}\bigl(0,5z + 19\tfrac{1}{2}\bigr) = \bigl(2\tfrac{7}{9}z + 3\tfrac{1}{3}\bigr)\times 1,2.\)
      Решение: \[ \tfrac{2}{3}\left(0{,}5z + 19{,}5\right) = \left(\tfrac{25}{9}z + \tfrac{10}{3}\right) \cdot \tfrac{6}{5} \] \[ \tfrac{1}{3}z + 13 = \tfrac{10}{3}z + 4 \quad \Rightarrow \quad -9z = -27 \quad \Rightarrow \quad z = 3. \] Ответ: \(\boxed{3}\).
   2. \((x^2 + 100)\,(4x + 5,36)\,(|5x| - 12) = 0.\)
      Решение:
      • \(x^2 + 100 = 0\): нет решений.
      • \(4x + 5{,}36 = 0 \Rightarrow x = -1{,}34\).
      • \(|5x| - 12 = 0 \Rightarrow x = \tfrac{12}{5} = 2{,}4\), или \(x = -\tfrac{12}{5} = -2{,}4\).
      Ответ: \(\boxed{-2{,}4}\), \(\boxed{-1{,}34}\), \(\boxed{2{,}4}\).
3. Площадь большого прямоугольника:
   Решение: Коэффициент подобия сторон \( \tfrac{24}{8} = 3 \).
   Отношение площадей: \(3^2 = 9\).
   Площадь большого прямоугольника: \(96 \cdot 9 = 864\) см².
   Ответ: \(\boxed{864}\) см².
4. Количество задач по дням:
   Решение:
   Всего задач: 150. Первый день: \(150 \cdot 0{,}24 = 36\).
   Остаток: \(150 - 36 = 114\).
   Второй день: \(\tfrac{2}{3}x\), третий день: \(x\), четвертый день: \(\tfrac{5}{12}x\), пятый день: \(\tfrac{5}{4}x\).
   Уравнение: \[ \tfrac{2}{3}x + x + \tfrac{5}{12}x + \tfrac{5}{4}x = 114 \quad \Rightarrow \quad \tfrac{19}{6}x = 114 \quad \Rightarrow \quad x = 36. \]
   Значения:
   • Первый день: 36
   • Второй день: 24
   • Третий день: 36
   • Четвертый день: 15
   • Пятый день: 45
   Ответ: 36, 24, 36, 15, 45.
5. Прямоугольник \(ABCD\):
   1. Координаты пересечений сторон:
      
      • Сторона \(AB\): горизонтальная линия \(y = 4\), пересекает ось \(OY\) в \((0; 4)\).
      • Сторона \(CD\): горизонтальная линия \(y = -2\), пересекает ось \(OY\) в \((0; -2)\).
      Ответ: \((0;4)\), \((0;-2)\).
   2. Новые координаты после переноса:
      Координаты центра \(A_1B_1C_1D_1\): \((-1;3)\), \((-7;3)\), \((-7;-3)\), \((-1;-3)\).
      Центр диагоналей: \(\left(\tfrac{-1 + (-7)}{2}; \tfrac{3 + (-3)}{2}\right) = (-4; 0)\).
      Ответ: \(\boxed{(-4; 0)}\).
6. Сумма целых чисел с произведением 1:
   Решение: Невозможно, так как количество отрицательных элементов должно быть чётным (их произведение равно \(1\)), но сумма чётного количества отрицательных чисел с остальными единицами не может дать ноль при нечётном количестве элементов \(2023\).
   Ответ: Нет.
7. Сумма чисел с произведением 54054:
   Решение: Разложение на множители: \(54054 = 2 \cdot 3^3 \cdot 7 \cdot 11 \cdot 13\).
   Числа: \(2\), \(3\), \(7\), \(9\), \(11\), \(13\).
   Сумма: \(2 + 3 + 7 + 9 + 11 + 13 = 45\).
   Ответ: \(\boxed{45}\).