8 800 707 6729
8 800 707 6729Telegram канал

Лицей КФУ из 6 в 7 класс 2020 год вариант 4

Сложность:
Дата экзамена: 2020
Печать
youit.school ©

ЛИЦЕЙ КФУ


2020 год


Вариант 4



  1. Уменьшить значение выражения на $20\%$: \[ \bigl(1\tfrac{2}{3}\cdot 2{,}1 - 4\bigr) \;:\; 1\tfrac{2}{3} \;+\; 1\tfrac{1}{6}. \]
    1. Упростите выражение и найдите его значение при \(y = 5\tfrac{1}{9}\): \[ -8\;\bigl(\tfrac{1}{8} - \tfrac{1}{4}y\bigr) \;-\; 3\;\bigl(1 - 2\tfrac{1}{3}y\bigr). \]
    2. Разделить полученное число в отношении \[ 0{,}5 : \tfrac{2}{3}. \]
  3. Решить уравнения:
    1. \(\displaystyle \frac{-0{,}8}{1{,}2x + 2{,}8} \;=\; \frac{3}{4x - 2};\)
    2. \(\displaystyle \bigl|\;|2x - 7| - 4{,}5\bigr|\;\cdot\;(12x - 4) \;=\; 0.\)
  4. Решите задачи:
    1. Найдите три числа, если первое относится ко второму как \(2:3\), второе к третьему как \(\tfrac{2}{3}:1{,}6\), а сумма наибольшего и наименьшего чисел равна \(46\).
    2. В первом томе трёхтомного издания \(Y\) страниц. Второй том по объёму больше первого на \(20\%\), а третий том составляет \(\tfrac{2}{3}\) первого. Сколько страниц в трёх томах? Составьте выражение для решения задачи, упростите его и найдите значение при \(Y = 300\).
  5. Даны точки \(A(a; b)\), \(B(-a; b)\), \(C(a; -b)\), где \(a \neq 0\), \(b \neq 0\). Сделайте чертёж и найдите координаты точек пересечения сторон треугольника \(ABC\) с осями координат.
  6. Все натуральные числа от 1 до $14^2$ последовательно в порядке возрастания расставлены в клетки таблицы размером $14\times14$. Как нужно вычеркнуть одну строку и один столбец так, чтобы сумма всех оставшихся чисел была чётной?
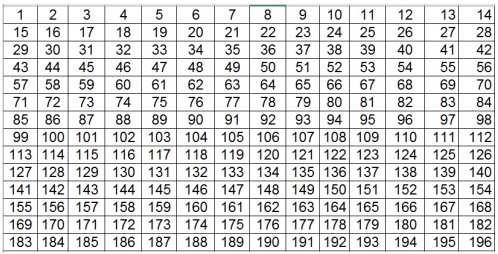    Для решения не требуется вычислять сами суммы. Нужно дать обоснование, показывающее, почему именно выбранная строка и столбец обеспечивают чётную сумму оставшихся чисел, и чётко сформулировать общее правило вычеркивания (частные примеры в качестве доказательства общего утверждения не принимаются).

  7. Известно, что \[ (a - b + 2005),\quad (b - c + 2005)\quad\text{и}\quad(c - a + 2005) \] являются тремя последовательными целыми числами. Найдите эти числа.


    Решение должно быть приведено в общем виде; ответы, полученные подбором, не принимаются. Числа $a,b,c$ определять не требуется.

Материалы школы Юайти
youit.school ©

Решения задач



  1. Уменьшить значение выражения на $20\%$: \[ \left(1\tfrac{2}{3} \cdot 2{,}1 - 4\right) : 1\tfrac{2}{3} + 1\tfrac{1}{6} \]
    Решение:
    Вычислим исходное выражение:
    $\left(\frac{5}{3} \cdot \frac{21}{10} - 4\right) : \frac{5}{3} + \frac{7}{6} = \left(\frac{7}{2} - 4\right) \cdot \frac{3}{5} + \frac{7}{6} = -\frac{1}{2} \cdot \frac{3}{5} + \frac{7}{6} = -\frac{3}{10} + \frac{7}{6} = \frac{13}{15}$.
    Уменьшим на 20\%: $\frac{13}{15} \cdot 0{,}8 = \frac{52}{75}$.
    Ответ: $\frac{52}{75}$.

    1. Упростить выражение: \[ -8\left(\frac{1}{8} - \frac{1}{4}y\right) - 3\left(1 - 2\tfrac{1}{3}y\right) \]
      Решение:
      $-8 \cdot \frac{1}{8} + 8 \cdot \frac{1}{4}y - 3 + 7y = -1 + 2y -3 +7y = -4 +9y$.
      Подставим $y = 5\tfrac{1}{9} = \frac{46}{9}$:
      $-4 + 9 \cdot \frac{46}{9} = -4 +46 =42$.
      Ответ: 42.
    2. Разделить число 42 в отношении $0{,}5 : \frac{2}{3}$.
      Решение:
      Приведём отношение к целым числам: $0{,}5 : \frac{2}{3} = 3 : 4$.
      Сумма частей: $3 +4 =7$. Каждая часть: $\frac{42}{7} =6$.
      Результат: $3 \cdot6 =18$ и $4 \cdot6 =24$.
      Ответ: 18 и 24.


  3. Решить уравнения:
    1. $\frac{-0{,}8}{1{,}2x +2{,}8} = \frac{3}{4x -2}$.
      Решение:
      Перекрёстное умножение: $-0{,}8(4x-2) =3(1{,}2x+2{,}8)$.
      $-3{,}2x +1{,}6 =3{,}6x +8{,}4 \implies -6{,}8x =6{,}8 \implies x =-1$.
      Проверка: Знаменатели не обращаются в ноль.
      Ответ: $-1$.
    2. $\left|\;|2x -7| -4{,}5\right| \cdot(12x -4) =0$.
      Решение:
      Произведение равно нулю, если:
      1) $12x -4 =0 \implies x =\frac{1}{3}$;
      2) $\left|\;|2x -7| -4{,}5\right|=0 \implies |2x -7|=4{,}5$.
      Решаем модуль:
      $2x-7=4{,}5 \implies x=5{,}75$;
      $2x-7=-4{,}5 \implies x=1{,}25$.
      Ответ: $x= \frac{1}{3}; 1{,}25; 5{,}75$.


  4. Решить задачи:
    1. Найти три числа в отношении $2:3$, $\frac{2}{3}:1{,}6$, сумма наибольшего и наименьшего равна 46.
      Решение:
      Приведём второе отношение: $\frac{2}{3}:1{,}6 =5:12$. Установим пропорции: $10:15:36$.
      Наибольшее + наименьшее: $10 +36 =46 \implies k=1$.
      Ответ: $10;15;36$.
    2. Объём трёхтомника при $Y =300$:
      Выражение: $Y +1{,}2Y +\frac{2}{3}Y =\frac{43}{15}Y$.
      Подстановка: $\frac{43}{15} \cdot300 =860$.
      Ответ: 860 страниц.


  5. Координаты точек пересечения сторон треугольника с осями:
    Решение:
    Сторона $AB$ пересекает ось $OY$ в $(0;b)$.
    Сторона $BC$ пересекает обе оси в $(0;0)$.
    Сторона $AC$ не пересекает оси.
    Ответ: $(0;b)$ и $(0;0)$.

  6. Стратегия удаления строки и столбца для чётной суммы:
    Решение:
    Сумма всех чисел таблицы чётная. Сумма вычеркнутых строки и столбца должна иметь ту же чётность, что и их пересечение. Выбираем строку и столбец с чётным числом на пересечении.
    Ответ: Вычеркнуть строку и столбец, пересекающиеся на чётном числе.

  7. Последовательные числа:
    Решение:
    Сумма данных выражений: $(a-b+2005)+(b-c+2005)+(c-a+2005) =6015$.
    Три последовательных числа: $2004,2005,2006$ (сумма $6015$).
    Ответ: $2004,2005,2006$.
Материалы школы Юайти