Лицей КФУ из 6 в 7 класс 2020 год вариант 3

ЛИЦЕЙ КФУ

2020 год

Вариант 3

1. Увеличить значение выражения на $40\%$: \[ 4{,}3 + 1{,}8\cdot\bigl(1\tfrac{2}{3}:2{,}5 - 2\bigr). \]
2. 1. Упростите выражение и найдите его значение при \(y = 4\tfrac{1}{3}\): \[ -6\cdot\Bigl(\tfrac{1}{6} - \tfrac{1}{3}y\Bigr) \;-\; 2\cdot\Bigl(1 - 3\tfrac{1}{2}y\Bigr). \]
   2. Разделите полученное число в отношении \[ 0{,}5 : 2\tfrac{1}{2}. \]
3. Решите уравнения:
   1. \(\displaystyle \frac{0{,}3}{0{,}5x - 3} = \frac{-6}{9x + 3};\)
   2. \(\displaystyle \bigl|\,3 - |x + 1|\,\bigr|\;\cdot\;(2x - 5) = 0.\)
4. Решите задачи:
   1. Длины сторон треугольника относятся как \(2:3:4\). Найдите периметр треугольника, если сумма наибольшей и наименьшей сторон равна \(18\) см.
   2. Мама поделила между тремя детьми купленные конфеты. Маше досталось \(\tfrac{5}{18}\) всех конфет, Ире — \(\tfrac{8}{13}\) оставшихся, а остальные \(X\) грамм конфет достались Юре. Выразите через \(X\) массу конфет, доставшихся девочкам, упростите выражение и найдите его значение при \(X = 200\).
5. Даны точки \(A(a; b)\), \(B(-a; -b)\), \(C(-a; 3b)\), где \(a \neq 0\), \(b \neq 0\). Сделайте чертёж и найдите координаты точек пересечения сторон треугольника \(ABC\) с осями координат.
6. Все натуральные числа от 1 до $12^2$ последовательно в порядке возрастания расставлены в клетки таблицы размером $12\times12$. Как нужно вычеркнуть одну строку и один столбец так, чтобы сумма всех оставшихся чисел была чётной?
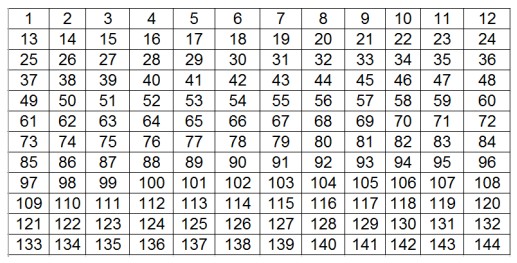   Для решения не требуется вычислять сами суммы. Нужно дать обоснование, показывающее, почему именно выбранная строка и столбец дают чётную сумму оставшихся чисел, и чётко сформулировать общее правило вычеркивания (частные примеры как доказательство не принимаются).
   
   
7. Известно, что \[ (a - b + 2020),\quad (b - c + 2020)\quad\text{и}\quad(c - a + 2020) \] — три последовательных целых числа. Найдите эти числа.
   
   
   Решение должно быть приведено в общем виде; ответы, полученные подбором, не принимаются. Числа $a,b,c$ определять не требуется.
   
   

Решения задач

1. Увеличить значение выражения на $40\%$: \[ 4{,}3 + 1{,}8\cdot\bigl(1\tfrac{2}{3}:2{,}5 - 2\bigr) = 4{,}3 + 1{,}8\cdot(0{,}666\ldots - 2) = 4{,}3 - 2{,}4 = 1{,}9 \] Увеличение на $40\%$: \[ 1{,}9 \cdot 1{,}4 = 2{,}66 \] Ответ: 2,66.
   
   
2. 1. Упрощаем выражение: \[ -6\cdot\Bigl(\tfrac{1}{6} - \tfrac{1}{3}y\Bigr) - 2\cdot\Bigl(1 - 3\tfrac{1}{2}y\Bigr) = -1 + 2y - 2 + 7y = 9y - 3 \] Подставляем \( y = 4\tfrac{1}{3} = \tfrac{13}{3} \): \[ 9 \cdot \tfrac{13}{3} - 3 = 39 - 3 = 36 \] Ответ: 36.
   2. Деление в отношении \( 0{,}5 : 2\tfrac{1}{2} = 1:5 \). Части: \[ \frac{36}{1+5} \cdot 1 = 6; \quad \frac{36}{6} \cdot 5 = 30 \] Ответ: 6 и 30.
   
   
   
3. Решаем уравнения:
   1. Перекрестное умножение: \[ 0{,}3(9x + 3) = -6(0{,}5x - 3) \implies 2{,}7x + 0{,}9 = -3x + 18 \implies 5{,}7x = 17{,}1 \implies x = 3 \] Ответ: 3.
   2. Произведение равно нулю: \[ 2x - 5 = 0 \implies x = 2{,}5 \] Проверка модуля: \[ |3 - |x + 1|| = 0 \implies |x + 1| = 3 \implies x = 2 \text{ или } x = -4 \] Эти корни не обращают \(2x - 5\) в ноль. Ответ: 2,5. Ответ: 2,5.
   
   
   
4. Решаем задачи:
   1. Отношение сторон \(2:3:4\). Часть \(2+4=6\) соответствует 18 см: \[ 1 \text{ часть} = 3 \text{ см}, \quad P = (2+3+4) \cdot 3 = 27 \text{ см} \] Ответ: 27 см.
   2. Масса конфет: \[ \text{Маша: } \tfrac{5}{18}M, \quad \text{Ира: } \tfrac{8}{13} \cdot \tfrac{13}{18}M = \tfrac{8}{18}M, \quad \text{Юра: } M - \tfrac{5}{18}M - \tfrac{8}{18}M = \tfrac{5}{18}M = X \] \[ M = \tfrac{18X}{5}, \quad \text{Девочки: } \tfrac{13X}{5} \quad (X = 200 \implies 520 \text{ г}) \] Ответ: \(\tfrac{13X}{5}\); 520 г.
   
   
   
5. Координаты точек пересечения:
   • Сторона \(AB\) пересекает оси в \((0; 0)\).
   • Сторона \(AC\): ось \(Ox\) — \((2a; 0)\), ось \(Oy\) — \((0; 2b)\).
   • Сторона \(BC\): параллельна оси \(Oy\), пересекает \(Ox\) в \((-a; 0)\).
   Ответ: \((0; 0)\), \((2a; 0)\), \((0; 2b)\).
   
   
6. Стратегия вычеркивания:
   • Все суммы строк и столбцов четные.
   • Удаление строки и столбца с четной суммой сохраняет четность суммы остатка, если их пересечение четное.
   • Ответ: Вычеркнуть строку и столбец, содержащие четное число на пересечении.
   
   
   
7. Пусть числа \(n-1\), \(n\), \(n+1\). Суммируем: \[ (a-b+2020) + (b-c+2020) + (c-a+2020) = 6060 = 3n \implies n = 2020 \] Числа: 2019, 2020, 2021. Ответ: 2019, 2020, 2021.