Лицей КФУ из 6 в 7 класс 2020 год вариант 2

ЛИЦЕЙ КФУ

2020 год

Вариант 2

1. Найдите число, 25% которого составляет значение выражения \[ \bigl(1\frac{1}{4}\cdot 2{,}6 - 4\bigr) : 1{,}2 + 0{,}9. \]
2. 1. Упростите выражение и найдите его значение при \(x = 10\frac{2}{5}\): \[ 5\;\bigl(\tfrac{2}{5}x - 0{,}7\bigr) - 3\;\bigl(\tfrac{1}{3}x - 0{,}2\bigr). \]
   2. Разделить полученное число в отношении \(\tfrac{1}{3}:0{,}5\).
3. Решить уравнения:
   1. \(\displaystyle \frac{4{,}1}{2x + 3} = \frac{-12{,}3}{x - 1};\)
   2. \(\displaystyle |\,1{,}2 - |x + 4|\,|\cdot(2x + 3) = 0.\)
4. Решите задачи:
   1. Найдите три числа, если первое число относится ко второму как \(3:4\), второе ко третьему как \(\tfrac{2}{3}:0{,}75\), а разность наибольшего и наименьшего чисел равна \(12\).
   2. В первый день заасфальтировали \(X\) км дороги, во второй день — на \(25\%\) больше, чем в первый, а в третий — \(\tfrac{6}{7}\) участка, заасфальтированного в первый день. Сколько километров дороги заасфальтировано за три дня? Составьте выражение для решения задачи, упростите его и найдите значение при \(X = 4\).
5. Даны точки \(A(a; b)\), \(B(-a; b)\), \(C(-a; -b)\), где \(a \neq 0\), \(b \neq 0\). Сделайте чертёж и найдите координаты точек пересечения сторон треугольника \(ABC\) с осями координат.
6. Все натуральные числа от 1 до $14^2$ последовательно в порядке возрастания расставлены в клетки таблицы размером $14\times14$. Как нужно вычеркнуть одну строку и один столбец так, чтобы сумма всех оставшихся чисел была чётной?
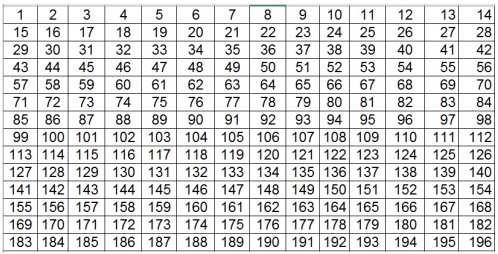   Для решения этой задачи нет необходимости точно считать суммы. Необходимо привести подробное обоснование, т.~е. объяснить, почему именно так надо вычеркивать (частные случаи как доказательство общего утверждения не принимаются) и чётко сформулировать общее правило вычеркивания.
   
   
7. Известно, что \[ (a - b + 2003),\quad (b - c + 2003)\quad\text{и}\quad(c - a + 2003) \] являются тремя последовательными целыми числами. Найдите эти числа.
   
   
   Решение необходимо привести в общем виде. Ответы, полученные с помощью подбора, не принимаются. Числа $a,b,c$ находить не нужно.

Решения задач

1. Найдите число, 25% которого составляет значение выражения \[ \bigl(1\frac{1}{4}\cdot 2{,}6 - 4\bigr) : 1{,}2 + 0{,}9. \]
   Решение: \[ \bigl(\tfrac{5}{4} \cdot 2{,}6 - 4\bigr) : 1{,}2 + 0{,}9 = \bigl(3{,}25 - 4\bigr) : 1{,}2 + 0{,}9 = (-0{,}75) : 1{,}2 + 0{,}9 = -0{,}625 + 0{,}9 = 0{,}275 \] Искомое число: $0{,}275 \cdot 4 = 1{,}1$ (25% = $\frac{1}{4}$).
   Ответ: 1,1.
   
   
2. 1. Упростите выражение при \(x = 10\frac{2}{5}\): \[ 5\;\bigl(\tfrac{2}{5}x - 0{,}7\bigr) - 3\;\bigl(\tfrac{1}{3}x - 0{,}2\bigr) = 2x - 3{,}5 - x + 0{,}6 = x - 2{,}9 \] Подставляем \(x = 10{,}4\): \(10{,}4 - 2{,}9 = 7{,}5\).
      Ответ: 7,5.
      
      
   2. Разделить 7,5 в отношении \(\tfrac{1}{3}:0{,}5 = 2:3\): \[ 7{,}5 \cdot \tfrac{2}{5} = 3;\quad 7{,}5 \cdot \tfrac{3}{5} = 4{,}5 \] Ответ: 3 и 4,5.
   
   
   
3. Решить уравнения:
   1. \(\displaystyle \frac{4{,}1}{2x + 3} = \frac{-12{,}3}{x - 1}\)
      Решение: \[ 4{,}1(x - 1) = -12{,}3(2x + 3) \quad \Rightarrow \quad x - 1 = -3(2x + 3) \] \[ x - 1 = -6x - 9 \quad \Rightarrow \quad 7x = -8 \quad \Rightarrow \quad x = -\tfrac{8}{7} \] Проверка: знаменатели не обращаются в ноль.
      Ответ: \(-\tfrac{8}{7}\).
      
      
   2. \(|\,1{,}2 - |x + 4|\,|\cdot(2x + 3) = 0\)
      Решение: Произведение равно нулю, если:
      • \(2x + 3 = 0 \Rightarrow x = -1{,}5\). Проверка модулей: \(|1{,}2 - |{-1{,}5 + 4}|| = |1{,}2 - 2{,}5| = 1{,}3 \neq 0\) — не подходит.
      • \(|1{,}2 - |x + 4|| = 0 \Rightarrow |x + 4| = 1{,}2 \Rightarrow x + 4 = \pm1{,}2\) \[ x = -5{,}2 \quad \text{или} \quad x = -2{,}8 \]
      Ответ: \(-5{,}2\) и \(-2{,}8\).
   
   
   
4. Решите задачи:
   1. Пусть числа \(3k\), \(4k\), \(9k\). Отношение \(4k:\frac{2}{3}/\frac{3}{4} = 4k: \frac{8}{9} = 9k\). Разность \(9k - 3k = 6k = 12 \Rightarrow k = 2\). \[ \text{Числа: } 6,\ 8,\ 18 \] Ответ: 6, 8, 18.
      
      
   2. Выражение: \[ X + 1{,}25X + \tfrac{6}{7}X = X(1 + 1{,}25 + \tfrac{6}{7}) = X \cdot \tfrac{231}{84} = 4 \cdot \tfrac{231}{84} = 11 \] Ответ: 11 км.
   
   
   
5. Координаты точек пересечения:
   • Сторона AB пересекает ось Y в (0; b)
   • Сторона BC пересекает ось X в (-a; 0)
   • Сторона AC пересекает оси в начале координат (0;0)
   Ответ: (0; b), (-a; 0), (0;0).
   
   
6. Сумма всех чисел: \(\tfrac{(14^2)(14^2 + 1)}{2}\). Четность суммы зависит от количества нечётных чисел. При удалении строки и столбца с нечётной суммой общая чётность сохранится.
   Ответ: нужно удалить строку и столбец с одинаковой чётностью суммы.
   
   
7. Пусть числа \(n-1\), \(n\), \(n+1\). Из условий: \[ \begin{cases} (a - b + 2003) = n-1 \\ (b - c + 2003) = n \\ (c - a + 2003) = n+1 \end{cases} \] Складываем уравнения: \(0 + 6009 = 3n \Rightarrow n = 2003\). Числа: 2002, 2003, 2004.
   Ответ: 2002, 2003, 2004.