Лицей КФУ из 5 в 6 класс 2018 год вариант 1

ЛИЦЕЙ КФУ

2018 год

Вариант 1

1. Найдите значение выражения \[ 161 - \bigl(469{,}7 : 15{,}4 + 9{,}52\bigr) * 1{,}5. \]
2. Решите уравнение:
   1. \(12 - 7\dfrac{3}{4} + x + 4\dfrac{1}{4} = 12\dfrac{1}{2}.\)
   2. \(24{,}8 : (6{,}08x - 20{,}8) * 2{,}7 = 1{,}674.\)
3. В январе рабочий недовыполнил план на $5\%$, а в феврале перевыполнил тот же план на $7\%$, собрав на 24 прибора больше, чем в январе. Сколько приборов собрал рабочий в январе и сколько – в феврале?
4. От пристани \(A\) к пристани \(B\), расстояние до которой равно 28,8 км, отправился плот. Через 0,4 часа навстречу ему от пристани \(B\) вышел катер, собственная скорость которого равна 17,5 км/ч, и встретился с плотом через 1,6 часа. Найдите скорость течения реки.
5. 1. Какая из линий самая короткая? Объясните ответ.
      
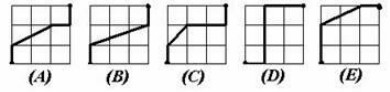
   2. Как тремя прямолинейными разрезами разделить круглый торт на семь частей?

1. Задумано натуральное двузначное число, которое на 66 больше произведения своих цифр. Какое число задумано?
2. Можно ли числа \(1,2,\dots,31\) разбить на несколько групп так, чтобы в каждой группе максимальное число равнялось сумме всех остальных?

Решения задач

1. Найдите значение выражения \[ 161 - \left(469{,}7 : 15{,}4 + 9{,}52\right) \cdot 1{,}5. \]
   Решение: \[ 469{,}7 : 15{,}4 = 30{,}5 \] \[ 30{,}5 + 9{,}52 = 40{,}02 \] \[ 40{,}02 \cdot 1{,}5 = 60{,}03 \] \[ 161 - 60{,}03 = 100{,}97 \] Ответ: 100,97.
   
   
2. Решите уравнение:
   1. \( 12 - 7\dfrac{3}{4} + x + 4\dfrac{1}{4} = 12\dfrac{1}{2}. \)
      Решение: \[ 12 - 7{,}75 + x + 4{,}25 = 12{,}5 \] \[ 8{,}5 + x = 12{,}5 \] \[ x = 12{,}5 - 8{,}5 = 4 \] Ответ: 4.
      
      
   2. \( 24{,}8 : (6{,}08x - 20{,}8) \cdot 2{,}7 = 1{,}674. \)
      Решение: \[ (24{,}8 : (6{,}08x - 20{,}8)) \cdot 2{,}7 = 1{,}674 \] \[ 24{,}8 : (6{,}08x - 20{,}8) = 1{,}674 : 2{,}7 = 0{,}62 \] \[ 6{,}08x - 20{,}8 = 24{,}8 : 0{,}62 = 40 \] \[ 6{,}08x = 60{,}8 \] \[ x = \frac{60{,}8}{6{,}08} = 10 \] Ответ: 10.
   
   
   
3. В январе рабочий недовыполнил план на $5\%$, а в феврале перевыполнил тот же план на $7\%$, собрав на 24 прибора больше, чем в январе. Сколько приборов собрал рабочий в январе и сколько – в феврале?
   Решение: Пусть план — \(N\) приборов. \[ 0{,}07N - (-0{,}05N) = 0{,}12N = 24 \] \[ N = 24 : 0{,}12 = 200 \]
   В январе собрано: \[ 0{,}95N = 0{,}95 \cdot 200 = 190 \; \text{приборов} \] В феврале собрано: \[ 1{,}07N = 1{,}07 \cdot 200 = 214 \; \text{приборов} \] Ответ: В январе — 190, в феврале — 214.
   
   
4. От пристани \(A\) к пристани \(B\), расстояние до которой равно 28,8 км, отправился плот. Через 0,4 часа навстречу ему от пристани \(B\) вышел катер, собственная скорость которого равна 17,5 км/ч, и встретился с плотом через 1,6 часа после старта катера. Найдите скорость течения реки.
   Решение: Скорость течения (плота): \(v\) км/ч. Время движения плота до встречи: \(0{,}4 + 1{,}6 = 2\) часа.
   Катер двигался со скоростью \(17{,}5 - v\) км/ч против течения. \[ 2v + 1{,}6(17{,}5 - v) = 28{,}8 \] \[ 0{,}4v + 28 = 28{,}8 \] \[ v = \frac{0{,}8}{0{,}4} = 2 \; \text{км/ч}. \] Ответ: 2 км/ч.
   
   
5. 1. Какая из линий самая короткая? Объясните ответ.
      Линии, изображенные на рисунке, подлежат сравнению по длине. Для определения нельзя предоставить точный ответ без визуальной информации.
   2. Как тремя прямолинейными разрезами разделить круглый торт на семь частей?
      Решение: Сделать два перпендикулярных разреза через центр торта (получим 4 части), третий разрез провести так, чтобы он пересек три из четырёх кусков, добавив ещё три части. Итого: \(4 + 3 = 7\).

1. Задумано натуральное двузначное число, которое на 66 больше произведения своих цифр. Какое число задумано?
   Решение: Пусть число — \(10a + b\) (\(a\) — десятки, \(b\) — единицы). \[ 10a + b = ab + 66 \] Подбором: \[ a = 8, \quad b = 2 \quad \Rightarrow \quad 82 = 8 \cdot 2 + 66 = 16 + 66 = 82 \] Ответ: 82.
   
   
2. Можно ли числа \(1,2,\dots,31\) разбить на несколько групп так, чтобы в каждой группе максимальное число равнялось сумме всех остальных?
   Решение: Невозможно, так как число 31 превышает сумму всех меньших чисел (\(1 + 2 + \dots + 30 = 465\)). Сумма всех остальных чисел группы с 31 должна быть равна ему (\(465 \ne 31\)), что противоречит условию. Ответ: Нельзя.