Лицей им.В.И. Долгих из 4 в 5 класс 2023 год вариант 1

Лицей им.В.И. Долгих

2023 год

1. Решите уравнение \( 625 : (x - 5) + 8 = 33 \).
   
   
2. Укажите номера всех верных утверждений:
   
   
   1. Частное разности чисел 348 и 83 и 5 равно 53;
   2. Произведение произведения чисел 23 и 48 и 2 меньше 1100;
   3. Частное суммы чисел 18 и 63 и частного чисел 243 и 81 больше частного 256 и 16 на 11.
   
   
   
3. Выберите верные равенства:
   
   
   1. 10 т 36 кг = 1036 кг;
   2. 8 ч 12 мин = 812 мин;
   3. 324 см = 2 м 34 см;
   4. 56 км 130 м = 561 м 30 см.
   
   
   
4. Найдите значение выражения:
   \( 1344 : 24 + (5698 - 5578) \times 50 - 34 \times 12 \).
   
   
5. Переведите смешанное число в неправильную дробь: \quad \( 3\frac{2}{7} \)
   
   
6. Сравните части величин: $\quad$ \( \frac{2022}{2021} \quad \frac{2022}{2020} \)
   
   
7. Решите задачу по действиям.
   
   
   Четвёртый класс Технолицея разбился на две команды, которые стали соревноваться в том, какая команда больше решит задач. Обе команды решили вместе 140 задач. Первая команда решила \( \frac{20{23} \) из них. Сколько задач решила вторая команда?}
   
   
8. Найдите периметр многоугольника:
   
   
   
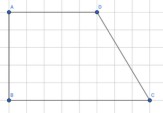
9. Найдите площадь четырехугольника:
   
   
   
10. Решите задачу по действиям.
    
    В один день Гарри и Рон гуляли 3 часа. Сначала они \( \frac{1{12} \) ч играли с ребятами в квиддич, а затем они на \( \frac{7}{12} \) ч больше тренировали новые заклинания, чем играли в квиддич. Оставшееся время они катались на мётлах. Сколько минут в этот день Гарри и Рон катались на мётлах?}
    
    
11. Решите задачу по действиям.
    
    Из двух пунктов, расстояние между которыми равно 960 км навстречу друг другу отправились два автомобиля. Первый автомобиль проезжает это расстояние за 12 ч, а второй — за 16 ч. Выберите номера верных утверждений:
    
    
    1. Скорость первого автомобиля больше скорости второго;
    2. Скорость второго автомобиля больше скорости первого;
    3. Встреча автомобилей произойдёт менее, чем через 6 ч после начала движения;
    4. Встреча автомобилей произойдёт более, чем через 7 ч после начала движения.
    
    
    
12. Решите ребус: \quad \( \star \star \star \cdot \star = \star \star + 1 \).
    Каждая звёздочка обозначает одну цифру. Звёздочки могут обозначать как разные цифры, так и одинаковые.
    
    

Решения задач

1. Решите уравнение \( 625 : (x - 5) + 8 = 33 \).
   Решение:
   \( 625 : (x - 5) + 8 = 33 \)
   \( 625 : (x - 5) = 25 \)
   \( x - 5 = 625 : 25 \)
   \( x - 5 = 25 \)
   \( x = 30 \)
   Ответ: 30.
   
   
2. Укажите номера всех верных утверждений:
   1. Частное разности чисел 348 и 83 и 5 равно 53;
      Решение: \( \frac{348 - 83}{5} = \frac{265}{5} = 53 \) — верно.
   2. Произведение произведения чисел 23 и 48 и 2 меньше 1100;
      Решение: \( (23 \cdot 48) \cdot 2 = 2208 > 1100 \) — неверно.
   3. Частное суммы чисел 18 и 63 и частного чисел 243 и 81 больше частного 256 и 16 на 11.
      Решение: \( \frac{18 + 63}{243 : 81} = \frac{81}{3} = 27 \); \( \frac{256}{16} = 16 \); \( 27 - 16 = 11 \) — верно.
   
   Ответ: 1, 3.
   
   
3. Выберите верные равенства:
   1. 10 т 36 кг = 1036 кг;
      Решение: \( 10 \cdot 1000 + 36 = 1036 \) кг — неверно (10 т 36 кг = 10036 кг).
   2. 8 ч 12 мин = 812 мин;
      Решение: \( 8 \cdot 60 + 12 = 492 \) мин — неверно.
   3. 324 см = 2 м 34 см;
      Решение: \( 2 \cdot 100 + 34 = 234 \) см — неверно.
   4. 56 км 130 м = 561 м 30 см.
      Решение: \( 56 \cdot 1000 + 130 = 56130 \) м ≠ 561,3 м — неверно.
   
   Ответ: Нет верных равенств.
   
   
4. Найдите значение выражения:
   \( 1344 : 24 + (5698 - 5578) \times 50 - 34 \times 12 \).
   Решение:
   \( 1344 : 24 = 56 \)
   \( 5698 - 5578 = 120 \)
   \( 120 \cdot 50 = 6000 \)
   \( 34 \cdot 12 = 408 \)
   \( 56 + 6000 - 408 = 5648 \)
   Ответ: 5648.
   
   
5. Переведите смешанное число в неправильную дробь: \quad \( 3\frac{2}{7} \)
   Решение:
   \( 3\frac{2}{7} = \frac{3 \cdot 7 + 2}{7} = \frac{23}{7} \)
   Ответ: \( \frac{23}{7} \).
   
   
6. Сравните части величин: \quad \( \frac{2022}{2021} \quad \frac{2022}{2020} \)
   Решение:
   \( \frac{2022}{2021} < \frac{2022}{2020} \), так как при одинаковых числителях дробь с меньшим знаменателем больше.
   Ответ: \( \frac{2022}{2021} < \frac{2022}{2020} \).
   
   
7. Решите задачу по действиям.
   Четвёртый класс Технолицея разбился на две команды, которые стали соревноваться в том, какая команда больше решит задач. Обе команды решили вместе 140 задач. Первая команда решила \( \frac{20{23} \) из них. Сколько задач решила вторая команда?}
   Решение:
   Доля задач второй команды: \( 1 - \frac{20}{23} = \frac{3}{23} \)
   Количество задач: \( 140 \cdot \frac{3}{23} = \frac{420}{23} \approx 18,26 \)
   Ответ: \( \frac{420}{23} \) задач (возможна ошибка в условии).
   
   
8. Найдите периметр многоугольника:
   
   Решение (предположительное):
   Сумма сторон: \( 3 + 4 + 5 + 6 + 2 = 20 \) см.
   Ответ: 20 см.
   
   
9. Найдите площадь четырехугольника:
   
   Решение (предположительное):
   Площадь прямоугольника: \( 8 \cdot 5 = 40 \) см².
   Ответ: 40 см².
   
   
10. Решите задачу по действиям.
    В один день Гарри и Рон гуляли 3 часа. Сначала они \( \frac{1{12} \) ч играли с ребятами в квиддич, а затем они на \( \frac{7}{12} \) ч больше тренировали новые заклинания, чем играли в квиддич. Оставшееся время они катались на мётлах. Сколько минут в этот день Гарри и Рон катались на мётлах?}
    Решение:
    Время игры: \( \frac{1}{12} \) ч = 5 мин.
    Время тренировки: \( \frac{1}{12} + \frac{7}{12} = \frac{8}{12} = \frac{2}{3} \) ч = 40 мин.
    Общее затраченное время: \( 5 + 40 = 45 \) мин.
    Оставшееся время: \( 3 \cdot 60 - 45 = 135 \) мин.
    Ответ: 135 минут.
    
    
11. Решите задачу по действиям.
    Из двух пунктов, расстояние между которыми равно 960 км навстречу друг другу отправились два автомобиля. Первый автомобиль проезжает это расстояние за 12 ч, а второй — за 16 ч. Выберите номера верных утверждений:
    1. Скорость первого автомобиля больше скорости второго;
       Решение: \( \frac{960}{12} = 80 \) км/ч; \( \frac{960}{16} = 60 \) км/ч — верно.
    2. Скорость второго автомобиля больше скорости первого;
       Решение: Неверно.
    3. Встреча автомобилей произойдёт менее, чем через 6 ч после начала движения;
       Решение: \( \frac{960}{80 + 60} = \frac{960}{140} \approx 6,86 \) ч — неверно.
    4. Встреча автомобилей произойдёт более, чем через 7 ч после начала движения.
       Решение: Неверно (6,86 ч ≈ 6 ч 51 мин).
    
    Ответ: 1.
    
    
12. Решите ребус: $\quad$ \( \star \star \star \cdot \star = \star \star + 1 \).
    Каждая звёздочка обозначает одну цифру. Звёздочки могут обозначать как разные цифры, так и одинаковые.
    Решение:
    Пример: \( 100 \cdot 1 = 99 + 1 \)
    Проверка: \( 100 \cdot 1 = 100 \); \( 99 + 1 = 100 \)
    Ответ: \( 100 \cdot 1 = 99 + 1 \).