Лицей 214 из 9 в 10 класс 2021 год (вариант1)

ЛИЦЕЙ №214 СПБ

2021 год

Вариант 1

1. Решите уравнения: \[ \frac{5x+4}{2} + 3 = \frac{9x}{4}, \qquad x^2 = 2x + 8. \]
2. Найдите значения выражений:
   1. \(18\cdot\bigl(\tfrac{1}{9}\bigr)^{2}\;-\;20\cdot\tfrac{1}{9}.\)
   2. \(3\cdot10^{-1} \;+\; 1\cdot10^{-2} \;+\; 5\cdot10^{-4}.\)
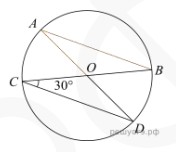
3. В окружности с центром в точке \(O\) проведены диаметры \(AD\) и \(BC\), угол \(OCD\) равен \(30^\circ\). Найдите величину угла \(OAB\).
   
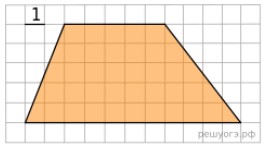
4. Найдите площадь трапеции, изображённой на рисунке.
   
5. Укажите номера верных утверждений:
   1. Существует квадрат, который не является прямоугольником.
   2. Если два угла треугольника равны, то равны и противолежащие им стороны.
   3. Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
   Если верных утверждений несколько, запишите их номера в порядке возрастания.
6. Упростите выражение \[ \frac{a^2 + 4a}{a^2 + 8a + 16} \] и найдите его значение при \(a = -2\). В ответ запишите полученное число.
7. На координатной прямой отмечены числа \(a\) и \(b\), расположенные слева от \(-1\) так, что \(a < b\). Какое из следующих утверждений неверно?
   1. \(a + b < 0;\)
   2. \(-2 < b - 1 < -1;\)
   3. \(a^2 b < 0;\)
   4. \(-a < 0.\)
8. Коля выбирает трёхзначное число. Найдите вероятность того, что оно делится на 5.

Решения задач

1. Решите уравнения:
   1. $\frac{5x+4}{2} + 3 = \frac{9x}{4}$
      Решение: Умножим обе части уравнения на 4:
      $2(5x + 4) + 12 = 9x$
      $10x + 8 + 12 = 9x$
      $10x + 20 = 9x$
      $10x - 9x = -20$
      $x = -20$
      Ответ: $-20$.
      
      
   2. $x^2 = 2x + 8$
      Решение: Перенесем все слагаемые в левую часть:
      $x^2 - 2x - 8 = 0$
      Дискриминант: $D = 4 + 32 = 36$
      Корни:
      $x = \frac{2 \pm 6}{2} \Rightarrow x_1 = 4$, $x_2 = -2$
      Ответ: 4; $-2$.
   
   
   
2. Найдите значения выражений:
   1. $18 \cdot \left(\frac{1}{9}\right)^{2} - 20 \cdot \frac{1}{9}$
      Решение:
      $18 \cdot \frac{1}{81} - \frac{20}{9} = \frac{2}{9} - \frac{20}{9} = -\frac{18}{9} = -2$
      Ответ: $-2$.
      
      
   2. $3 \cdot 10^{-1} + 1 \cdot 10^{-2} + 5 \cdot 10^{-4}$
      Решение:
      $0,3 + 0,01 + 0,0005 = 0,3105$
      Ответ: 0,3105.
   
   
   
3. В окружности диаметры $AD$ и $BC$, $\angle OCD = 30^\circ$. Найдите $\angle OAB$.
   Решение: Треугольник $OCD$ — равнобедренный ($OC = OD$ как радиусы).
   $\angle OCD = 30^\circ \Rightarrow \angle COD = 180^\circ - 2 \cdot 30^\circ = 120^\circ$
   Дуга $CD$ равна $120^\circ$. Так как $BC$ — диаметр, дуга $BOC$ составляет $180^\circ$.
   $\angle OAB$ опирается на дугу $OB$, которая равна $\frac{180^\circ - 120^\circ}{2} = 30^\circ$
   Ответ: $30^\circ$.
   
   
4. Найдите площадь трапеции.
   Решение: Основания трапеции 9 см и 17 см, высота 8 см. Площадь:
   $S = \frac{9 + 17}{2} \cdot 8 = 13 \cdot 8 = 104$ (см²)
   Ответ: 104 см².
   
   
5. Укажите верные утверждения:
   Решение:
   1. Неверно. Квадрат всегда является прямоугольником.
   2. Верно. По теореме о равенстве сторон против равных углов.
   3. Верно. Свойство параллельных прямых.
   Ответ: 2; 3.
   
   
6. Упростите выражение $\frac{a^2 + 4a}{a^2 + 8a + 16}$ при $a = -2$.
   Решение:
   $\frac{a(a + 4)}{(a + 4)^2} = \frac{a}{a + 4}$
   Подставляем $a = -2$:
   $\frac{-2}{-2 + 4} = \frac{-2}{2} = -1$
   Ответ: $-1$.
   
   
7. На координатной прямой $a < b < -1$. Неверное утверждение:
   Решение: Проверим пункты:
   1. Верно: сумма отрицательных чисел отрицательна.
   2. Верно: $b - 1 < -1 - 1 = -2$ → $-2 < b - 1 < -1$ неверно.
   3. Верно: $a^2$ положительно, $b$ отрицательно → произведение отрицательно.
   4. Неверно: $-a > 0$, так как $a$ отрицательно.
   Ответ: 4.
   
   
8. Вероятность, что трёхзначное число делится на 5.
   Решение: Всего трёхзначных чисел: $999 - 100 + 1 = 900$. Числа, делящиеся на 5: последняя цифра 0 или 5.
   Количество: $9 \cdot 10 \cdot 2 = 180$ (первые две цифры любые, третья — 0 или 5).
   Вероятность: $\frac{180}{900} = 0,2$
   Ответ: 0,2.