8 800 707 6729
8 800 707 6729Telegram канал

Лицей 214 из 9 в 10 класс 2019 год Вариант1

Сложность:
Дата экзамена: 2019
Печать
youit.school ©

ЛИЦЕЙ №214 СПБ


2019 год


Вариант 1



1 раздел – алгебра включает в себя

Числа и вычисления

  1. Вычислите \[ 17 \cdot \frac{5}{9} \;-\; 0,28 : \frac{1}{5} \;-\; 13,4 \cdot \frac{5}{9}. \]
  2. Вычислите \[ \bigl(-\tfrac{5}{9} + \tfrac{2}{15}\bigr) :\; 3,2 \cdot 0,18. \]
  3. Вычислите \[ \frac{49^4 \cdot 3^5}{147^3}. \]
  4. Найдите неизвестный член пропорции \[ 8 : 5 = x : 15. \]
  5. Вычислите \[ (\sqrt{2,5})^2 \;-\; \sqrt{3}\,\sqrt{0,12} \;+\; \frac{\sqrt{2}}{8}. \]
  6. Вычислите \[ \sqrt{48} + \sqrt{75} - \sqrt{108}. \]


1.2 Текстовые задачи

  1. Андрей старше Олега на 4 года, а Олег старше Бориса в 1,5 раза. Вместе им 36 лет. Сколько лет Олегу?
  2. В зале расставили одинаковыми рядами 72 стула. Рядов оказалось на 6 больше, чем стульев в каждом ряду. Сколько стульев в каждом ряду и сколько всего рядов?
  3. Стоимость проезда в пригородном автобусе составляет 60 рублей. Пенсионерам и детям до 10 лет предоставляется скидка $50\%$. Сколько рублей стоит проезд группы из 3 пенсионеров и 4 школьников: семи, девяти, двенадцати и четырнадцати лет?
  4. В девятых и седьмых классах школы 144 ученика. Число учащихся седьмых классов составляет 80% числа учащихся девятых классов. Сколько в школе семиклассников?
  5. Два мотоциклиста отправляются навстречу друг другу одновременно из двух пунктов, расстояние между которыми равно 200 км, и встречаются через 4 ч. Определите скорость каждого мотоциклиста, если скорость у одного из них на 10 км/ч больше, чем у другого.
  6. Если велосипедист будет ехать со скоростью 12 км/ч, то он опоздает на 1 ч. Если же он будет ехать со скоростью 18 км/ч, то приедет на 1 ч раньше. С какой скоростью он должен ехать, чтобы приехать вовремя?
  7. Моторная лодка прошла 10 км по озеру и 4 км против течения реки, затратив на весь путь 1 ч. Найдите собственную скорость лодки, если скорость течения реки равна 3 км/ч.


Неравенства, например:

  1. Решите неравенство: \[ (\sqrt{7} - 4)\,(6x + 12) \;\ge\; 0. \]
  2. Решите неравенство: \[ (x + 4)^2 \;>\; 16 - x^2. \]
  3. Найдите область определения выражения: \[ \frac{\sqrt{3 - 2x - x^2}}{x}. \]


1.4 Функции и графики, например

  1. Постройте график функции \(y = 4 - x^2\). Укажите промежутки знакопостоянства функции.
  2. Постройте график функции \(y = x^2 - 4x\). Укажите промежутки убывания функции.
  3. На рисунке изображён график квадратичной функции \(y = f(x)\). Какие из следующих утверждений о данной функции неверны? Запишите их номера.
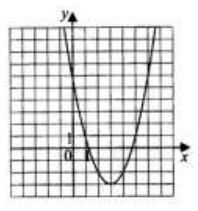
    1. \(f(1) > f(4)\).
    2. Функция возрастает на промежутке \((-\infty;3]\).
    3. Наименьшее значение функции равно 3.
  4. Найдите значение \(a\) по графику функции \(y = ax^2 + bx + c\), изображённому на рисунке.
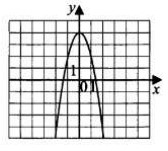
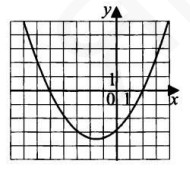
  5. На рисунке изображён график квадратичной функции \(y = f(x)\). Найдите наибольшее целое значение \(x\), при котором \(f(x) < 0\).
2 раздел — Геометрия включает в себя

Треугольники, например:

  1. В равнобедренном треугольнике \(ABC\) с основанием \(AB\) угол при вершине \(C\) равен \(68^\circ\). Найдите величину внешнего угла при вершине \(B\). Ответ дайте в градусах.
  2. В треугольнике \(ABC\) биссектрисы углов пересекаются в точке \(M\). Найдите угол \(\angle ABC\), если он составляет одну треть угла \(\angle AMC\). Ответ дайте в градусах.


2 раздел – геометрия включает в себя: Четырёхугольники, например:

  1. Один из углов ромба равен \(110^\circ\). Найдите угол между диагональю и стороной ромба. В ответе укажите меньший из них в градусах.
  2. В окружность вписан четырёхугольник, углы которого равны \(36^\circ\), \(72^\circ\), \(144^\circ\), \(108^\circ\). Найдите величину дуги, на которую опирается наибольший угол. Ответ дайте в градусах.
  3. Найдите углы вписанного в окружность четырёхугольника, если три его угла (в последовательном порядке) относятся как \(4:7:6\). В ответе укажите больший из них в градусах.


2.3 Площади фигур, например:

  1. В прямоугольнике одна сторона равна 80, а диагональ равна 82. Найдите площадь прямоугольника.
  2. В прямоугольнике диагональ равна 32, а угол между ней и одной из сторон равен \(60^\circ\). Найдите площадь прямоугольника, делённую на \(\sqrt{3}\).
  3. В равнобедренном треугольнике боковая сторона равна 44, основание — \(44\sqrt{3}\), а угол, лежащий против основания, равен \(120^\circ\). Найдите площадь треугольника.


2.4 Задания на выбор утверждений

  1. Выберите номера верных утверждений:
    1. В треугольнике против большей стороны лежит меньший угол.
    2. Сумма односторонних углов при пересечении двух параллельных прямых секущей меньше \(180^\circ\).
    3. Если углы при основании треугольника равны, то треугольник равнобедренный.
  2. Выберите номера неверных утверждений:
    1. Если две противоположные стороны четырёхугольника равны, то этот четырёхугольник — параллелограмм.
    2. Диагонали ромба делят углы ромба пополам.
    3. Трапеция равнобедренная, если её боковые стороны параллельны.
  3. Выберите номера верных утверждений:
    1. Серединный перпендикуляр к хорде проходит через центр окружности.
    2. Точка касания двух окружностей лежит на линии центров.
    3. Угол между двумя секущими, пересекающимися вне круга, равен полусумме дуг, высеченных секущими на окружности.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислите \[ 17 \cdot \frac{5}{9} - 0,28 : \frac{1}{5} - 13,4 \cdot \frac{5}{9}. \] Решение: \[ (17 - 13,4) \cdot \frac{5}{9} = 3,6 \cdot \frac{5}{9} = 2;\quad 0,28 : \frac{1}{5} = 1,4;\quad 2 - 1,4 = 0,6. \] Ответ: 0,6.

  2. Вычислите \[ \left(-\frac{5}{9} + \frac{2}{15}\right) : (3,2 \cdot 0,18). \] Решение: \[ -\frac{19}{45} : \frac{72}{125} = -\frac{2375}{3240}; \quad 3,2 \cdot 0,18 = 0,576. \] Ответ: -$\frac{475}{648}$ (≈−0,73).

  3. Вычислите \[ \frac{49^4 \cdot 3^5}{147^3}. \] Решение: \[ \frac{49^4 \cdot 3^5}{(49 \cdot 3)^3} = 49 \cdot 3^2 = 441. \] Ответ: 441.

  4. Найдите неизвестный член пропорции \[ 8 : 5 = x : 15. \] Решение: \[ x = \frac{8 \cdot 15}{5} = 24. \] Ответ: 24.

  5. Вычислите \[ (\sqrt{2,5})^2 - \sqrt{3} \cdot \sqrt{0,12} + \frac{\sqrt{2}}{8}. \] Решение: \[ 2,5 - 0,6 + \frac{\sqrt{2}}{8} ≈ 1,9 + 0,177 ≈ 2,077. \] Ответ: 2,08.

  6. Вычислите \[ \sqrt{48} + \sqrt{75} - \sqrt{108}. \] Решение: \[ 4\sqrt{3} + 5\sqrt{3} - 6\sqrt{3} = 3\sqrt{3}. \] Ответ: $3\sqrt{3}$.

  7. Андрей старше Олега на 4 года, а Олег старше Бориса в 1,5 раза. Вместе им 36 лет. Сколько лет Олегу? Решение: Пусть возраст Бориса – $x$, тогда Олегу – $1,5x$, Андрею – $1,5x +4$. \[ x + 1,5x + 1,5x +4 =36 \quad \Rightarrow x=12. \] Ответ: 12 лет.

  8. В зале расставили 72 стула одинаковыми рядами. Рядов оказалось на 6 больше, чем стульев в каждом ряду. Сколько стульев в ряду? Решение: Пусть $x$ стульев в ряду, тогда рядов $x+6$. \[ x(x +6) =72 \quad \Rightarrow x=6; \quad 12 рядов. \] Ответ:6 стульев,12 рядов.

  9. Стоимость проезда группы из 3 пенсионеров и 4 школьников. Решение: Пенсионеры: 3 ×30руб=90руб. Школьники до 10 лет:2 ×30=60руб; старшие:2 ×60=120руб. Всего:90+60+120=270руб. Ответ:270руб.

  10. В школе 144 ученика в 7 и 9 классах. Седьмых –80% девятых. Решение: Пусть девятых –$x$, седьмых –$0,8x$. \[ x +0,8x =1,8x =144 \quad \Rightarrow x=80; \quad седьмых –64. \] Ответ:64.

  11. Два мотоциклиста встретились через4 ч. Скорость одного на10 км/ч больше. Решение: Пусть скорости $v$ и $v +10$. \[ (v + v +10) \times4=200 \quad \Rightarrow2v=40 \quad \Rightarrow v=20км/ч. \] Ответ:20 и30км/ч.

  12. Велосипедист опоздает на1ч при12км/ч, приедет раньше на1ч при18км/ч. Решение:Пусть расстояние $S$. \[ S/12 = t +1; \quad S/18 = t −1 \quad \Rightarrow S=72км; t=5ч; \quad скорость=14,4км/ч. \] Ответ:14,4км/ч.

  13. Лодка прошла10км по озеру и4км против течения за1ч. Скорость течения3км/ч. Решение:Пусть скорость лодки$x$. \[ \frac{10}{x} + \frac{4}{x −3} =1 \quad \Rightarrow x=15км/ч. \] Ответ:15км/ч.

  14. Решите неравенство: $(√7 −4)(6x +12) ≥0$. Решение:$√7 ≈2,645 <4$, значит$(6x+12)≤0 \quad \Rightarrow x≤−2$. Ответ:$x∈(−\infty; −2]$.

  15. Решите неравенство: $(x +4)^2 >16 −x^2$. Решение: \[ x² +8x+16 >16−x² \quad \Rightarrow2x² +8x>0 \quad \Rightarrowx∈(−\infty;−4)∪(0;\infty). \] Ответ: $x∈(-\infty; -4)∪(0; +\infty)$.

  16. Найдите область определения выражения $\frac{\sqrt{3 - 2x -x²}}{x}$. Решение: \[ 3 −2x−x²≥0 \quad ⇒x∈[-3;1], \quad x≠0. \] Ответ: $x∈[-3;0)∪(0;1]$.

  17. В равнобедренном треугольнике угол при вершине68°. Внешний угол при основании. Решение: Угол основания:56°. Внешний угол:180°−56°=124°. Ответ:124°.

  18. Биссектрисы пересекаются в точкеM.УголABC составляет треть углаAMC. Решение:УголABC=x; уголAMC=90°+x/2. \[ x = \frac{1}{3}(90° +x/2) ⇒x=36°. \] Ответ:36°.

  19. Угол ромба110°. Найти угол между диагональю и стороной. Решение:Диагонали делят углы пополам. Меньший угол: \[ (180°−110°)/2=35°. \] Ответ:35°.

  20. Вписанный четырёхугольник с углами4:7:6. Больший угол. Решение: Сумма углов:4x+7x+6x+y=360°. Противоположные углы в сумме180°. \[ 4x+6x=10x=180° ⇒x=18°; ⇒больший угол7x=126°. \] Ответ:126°.

  21. Площадь прямоугольника со стороной80 и диагональю82. Решение: Вторая сторона√(82²−80²)=18. Площадь:80×18=1440. Ответ:1440.

  22. Диагональ32, угол60°. Площадь, делённая на√3. Решение:Стороны16 и16√3. Площадь:256√3 ⇒256. Ответ:256.

  23. Площадь равнобедренного треугольника с боковой44, основанием44√3, угол120°. Решение: Площадь=½×44×44×sin120°=484√3. Ответ:484√3.
Материалы школы Юайти