Лицей 214 из 9 в 10 класс 2017 год Вариант1
Печать
youit.school ©
ЛИЦЕЙ №214 СПБ
2017 год
Вариант 1
1 раздел — Алгебра включает в себя
1.1 Задания вычисительного характера, например:
- Найдите значение выражения \[ 0,13\cdot(-10)^3 + 4,6\cdot(-10)^2 \;-\; 870. \]
- Найдите значение выражения \[ \bigl(9,8\cdot10^{-2}\bigr)\,\bigl(3\cdot10^{-4}\bigr). \]
1.2 Задания на определение места точки на числовой оси или интервала числовой оси, например: Рассмотрим систему неравенств \[ \begin{cases} x > 9,\\ 8 - x < 0. \end{cases} \] На каком из следующих рисунков изображено множество её решений?

1.3 Применение метода интервалов, например:
- \(\displaystyle \frac{9 - 6x}{x + 1} \le 0.\)
- \(\displaystyle \frac{(x - 1)(3x - 8)}{6 - x} < 0.\)
- \(\displaystyle \frac{x(x - 2)}{1 + 4x} > 0.\)
- \(\displaystyle \frac{4x - 9x^2}{10 - x} \ge 0.\)
- \(\displaystyle \frac{x^2 - 25}{3 - x} > 0.\)
- \(\displaystyle \frac{8x^2 - 2}{3 - x} < 0.\)
- \(x^3 - 19x^2 + 84x \le 0.\)
- \(\displaystyle \frac{3x - 4}{x} \le -2.\)
1.4 Чтение графиков функций, например: На рисунке приведён график квадратичной функции \(y = f(x)\).
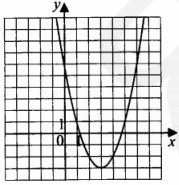
Какие из следующих утверждений о данной функции являются неверными? Запишите их номера.
- \(f(1) > f(4).\)
- Функция возрастает на промежутке \((-\infty, 3].\)
- Наименьшее значение функции равно 3.
1.5 Определение параметров и значений по графику
- Найдите значение \(a\) по графику функции
\[
y = a x^2 + b x + c,
\]
изображённому на рисунке.
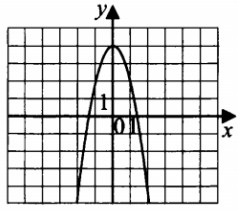
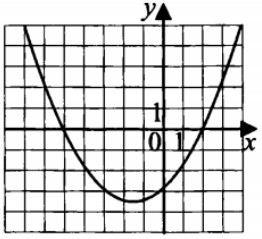
- На рисунке изображён график квадратичной функции \(y = f(x)\). Найдите наибольшее целое значение \(x\), при котором \(f(x) < 0\).
2 раздел — Геометрия включает в себя
2.1 Тема «Треугольники», например:
- (№11) В равнобедренном треугольнике \(ABC\) с основанием \(AB\) угол при вершине \(C\) равен \(68^\circ\). Найдите величину внешнего угла при вершине \(B\). Ответ дайте в градусах.
- (№12) В треугольнике \(ABC\) биссектрисы углов пересекаются в точке \(M\). Найдите угол \(\angle ABC\), если он составляет одну треть угла \(\angle AMC\). Ответ дайте в градусах.
2.2 Тема «Четырёхугольники», например:
- (№14) Один из углов ромба равен \(110^\circ\). Найдите угол между диагональю и стороной ромба. В ответе укажите меньший из них, в градусах.
- (№23) В окружность вписан четырёхугольник, углы которого равны \(36^\circ\), \(72^\circ\), \(144^\circ\), \(108^\circ\). Найдите величину дуги, на которую опирается больший из углов. Ответ дайте в градусах.
- (№31) Найдите углы вписанного в окружность четырёхугольника, если три его угла (в порядке обхода) относятся как \(4 : 7 : 6\). В ответе укажите наибольший из них в градусах.
2.3 Тема «Площади фигур», например:
- (№5) В прямоугольнике одна сторона равна 80, а диагональ равна 82. Найдите площадь прямоугольника.
- (№7) В прямоугольнике диагональ равна 32, а угол между ней и одной из сторон равен \(60^\circ\). Найдите площадь прямоугольника, делённую на \(\sqrt{3}\).
- (№42) В равнобедренном треугольнике боковая сторона равна 44, основание — \(44\sqrt{3}\), а угол, лежащий против основания, равен \(120^\circ\). Найдите площадь треугольника.
2.4 Задания на выбор утверждений
1. Выберите номера верных утверждений.
- В треугольнике против большей стороны лежит меньший угол.
- Сумма односторонних углов при пересечении двух параллельных прямых секущей меньше $180^\circ$.
- Если углы при основании треугольника равны, то треугольник равнобедренный.
2. Выберите номера неверных утверждений.
- Если две противоположные стороны четырёхугольника равны, то этот четырёхугольник — параллелограмм.
- Диагонали ромба делят углы ромба пополам.
- Трапеция равнобедренная, если её боковые стороны параллельны.
3. Выберите номера верных утверждений.
- Средний перпендикуляр к хорде проходит через центр окружности.
- Точка касания двух окружностей лежит на линии центров.
- Угол между двумя секущими, пересекающимися вне круга, равен полуразности дуг, высекаемых секущими на окружности.
Материалы школы Юайти
youit.school ©
Решения задач
- Найдите значение выражения:
\[
0,13\cdot(-10)^3 + 4,6\cdot(-10)^2 - 870
\]
Решение:
\[
0,13 \cdot (-1000) + 4,6 \cdot 100 - 870 = -130 + 460 - 870 = -540
\]
Ответ: -540.
- Найдите значение выражения:
\[
\bigl(9,8\cdot10^{-2}\bigr)\,\bigl(3\cdot10^{-4}\bigr)
\]
Решение:
\[
9,8 \cdot 3 \cdot 10^{-6} = 29,4 \cdot 10^{-6} = 2,94 \cdot 10^{-5}
\]
Ответ: \(2,94 \cdot 10^{-5}\).
- Решите систему неравенств:
\[
\begin{cases}
x > 9,\\
8 - x 9,\\
x > 8
\end{cases} \Rightarrow x > 9
\]
Ответ: Множество решений изображено на рисунке с интервалом \((9; +\infty)\).
- Решите неравенство:
\[
\frac{9 - 6x}{x + 1} \le 0
\]
Решение:
Нули числителя: \(x = 1,5\); нуль знаменателя: \(x = -1\). Метод интервалов:
Решение: \(x \in (-\infty; -1) \cup [1,5; +\infty)\). Ответ: \(x \in (-\infty; -1) \cup [1,5; +\infty)\).
- Анализ графика квадратичной функции:
- Утверждение 1: \(f(1) > f(4)\) — верно, так как \(x=1\) ближе к максимуму.
- Утверждение 2: Функция возрастает до \(x=3\) — верно для левой ветви.
- Утверждение 3: Наименьшее значение равно 3 — неверно, минимум ниже.
- Найдите параметр \(a\) по графику:
Вершина параболы в точке \((-1; -4)\). Формула вершины:
\[
x_{\text{верш}} = -\frac{b}{2a} \Rightarrow -1 = -\frac{b}{2a} \Rightarrow b = 2a
\]
Подстановка точки \((0; -3)\):
\[
y = a\cdot0^2 + 2a\cdot0 + c = -3 \Rightarrow c = -3
\]
Подстановка вершины:
\[
-4 = a(-1)^2 + 2a(-1) -3 \Rightarrow a = 1
\]
Ответ: \(a = 1\).
- Геометрическая задача (равнобедренный треугольник):
Угол при вершине \(C = 68^\circ\). Углы при основании:
\[
\frac{180^\circ - 68^\circ}{2} = 56^\circ
\]
Внешний угол при вершине \(B\):
\[
180^\circ - 56^\circ = 124^\circ
\]
Ответ: 124.
- Задача с ромбом:
Углы между диагональю и стороной:
\[
\frac{180^\circ - 110^\circ}{2} = 35^\circ \quad \text{и} \quad \frac{110^\circ}{2} = 55^\circ
\]
Ответ: 35.
- Площадь прямоугольника:
Стороны 80 и \(\sqrt{82^2 - 80^2} = 18\). Площадь:
\[
80 \cdot 18 = 1440
\]
Ответ: 1440.
- Верные утверждения:
- Верно: Если углы при основании равны, треугольник равнобедренный (3).
- Неверно: Против большей стороны лежит меньший угол (1).
- Верно: Точка касания на линии центров (2).
Материалы школы Юайти