Лицей 214 из 8 в 9 класс 2019 год (вариант1)

ЛИЦЕЙ №214 СПБ

Вариант 1

1. Числа и вычисления, например:
   $\frac{512^{-2} \cdot 128:\left(256^{-8} \cdot 64^{11}\right)}{4^{5} \cdot 2^{7} \cdot 16^{3}:\left(2^{6} \cdot 8\right)} ; 2 \sqrt{3,5}-0,5 \sqrt{56}+\sqrt{32}-3 \sqrt{3 \frac{5}{9}}$
   Найдите значение выражения $-16 a b+8(a+b)^{2}$ при $a=\sqrt{14}, b=\sqrt{5}$. Найдите допустимые значения переменной в выражении
   $\frac{3 x-4}{\sqrt{x}-3} \cdot \frac{3 x-6}{\sqrt{x-2}-3}$
   
2. Установите соответствие между графиками функций и формулами, которые их задают.
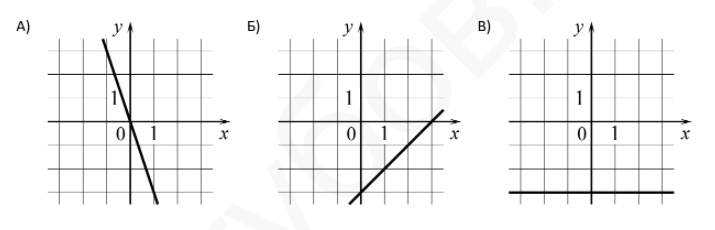
   1) $y=-3$ 2) $y=x-3$ 3) $y=-3 x$
3. В таблице под каждой буквой укажите соответствующий номер.
   Oтвет:
   
   

   $\mathrm{A}$	Б	$\mathrm{B}$

4. Текстовые задачи, например:
   1. Спортивный магазин проводит акцию. Любая футболка стоит 300 рублей. При покупке двух футболок - скидка на вторую футболку 70.
   Сколько рублей придётся заплатить за покупку двух футболок в период действия акции?
   2. На путь между двумя деревнями пешеход затратил на 4 ч 30 мин больше, чем мотоциклист. Скорость мотоциклиста 40 км/ч, скорость пешехода составляет 1/10 скорости мотоциклиста. Найдите расстояние между деревнями.

Решения задач

1. Найдите значение выражения:
   $\frac{512^{-2} \cdot 128:\left(256^{-8} \cdot 64^{11}\right)}{4^{5} \cdot 2^{7} \cdot 16^{3}:\left(2^{6} \cdot 8\right)}$
   Решение: Представим все числа как степени 2:
   $512 = 2^9,\ 128 = 2^7,\ 256 = 2^8,\ 64 = 2^6,\ 4 = 2^2,\ 16 = 2^4,\ 8 = 2^3$
   Числитель: $(2^9)^{-2} \cdot 2^7 : \left((2^8)^{-8} \cdot (2^6)^{11}\right) = 2^{-18} \cdot 2^7 : (2^{-64} \cdot 2^{66}) = 2^{-11} : 2^2 = 2^{-13}$
   Знаменатель: $(2^2)^5 \cdot 2^7 \cdot (2^4)^3 : (2^6 \cdot 2^3) = 2^{10} \cdot 2^7 \cdot 2^{12} : 2^9 = 2^{29} : 2^9 = 2^{20}$
   Итог: $\frac{2^{-13}}{2^{20}} = 2^{-33}$
   Ответ: $2^{-33}$.
   
   
2. Упростите выражение:
   $2 \sqrt{3,5} - 0,5 \sqrt{56} + \sqrt{32} - 3 \sqrt{3 \frac{5}{9}}$
   Решение:
   $2\sqrt{\frac{7}{2}} - 0,5 \cdot 2\sqrt{14} + 4\sqrt{2} - 3 \cdot \frac{4\sqrt{2}}{3} = \sqrt{14} - \sqrt{14} + 4\sqrt{2} - 4\sqrt{2} = 0$
   Ответ: 0.
   
   
3. Найдите значение выражения $-16ab + 8(a+b)^2$ при $a=\sqrt{14},\ b=\sqrt{5}$
   Решение: $-16\sqrt{14}\sqrt{5} + 8(\sqrt{14}+\sqrt{5})^2 = -16\sqrt{70} + 8(14 + 2\sqrt{70} + 5) = -16\sqrt{70} + 8(19 + 2\sqrt{70}) = 152 + 0 = 152$
   Ответ: 152.
   
   
4. Найдите допустимые значения переменной:
   $\frac{3x-4}{\sqrt{x}-3} \cdot \frac{3x-6}{\sqrt{x-2}-3}$
   Решение:
   1. $\sqrt{x} \geq 0 \Rightarrow x \geq 0$
   2. $\sqrt{x} \neq 3 \Rightarrow x \neq 9$
   3. $\sqrt{x-2} \geq 0 \Rightarrow x \geq 2$
   4. $\sqrt{x-2} \neq 3 \Rightarrow x \neq 11$
   5. $3x-6 \neq 0 \Rightarrow x \neq 2$
   Объединяя условия: $x \in [2;9) \cup (9;11) \cup (11;+\infty)$
   Ответ: $x \in [2;9) \cup (9;11) \cup (11;+\infty)$.
   
   
5. Установите соответствие между графиками:

   А	Б	В
   1	3	2

   Обоснование:
   А — горизонтальная прямая $y=-3$ (1)
   Б — прямая через начало координат $y=-3x$ (3)
   В — прямая с угловым коэффициентом 1 $y=x-3$ (2)
   
   
6. Решите задачи:
   1. Стоимость двух футболок:
      Первая футболка: 300 руб.
      Вторая футболка: 300 $\cdot$ 0,3 = 90 руб.
      Итого: 300 + 90 = 390 руб.
      Ответ: 390.
      
      
   2. Пусть расстояние $S$ км.
      Скорость пешехода: $\frac{40}{10} = 4$ км/ч
      Время пешехода: $\frac{S}{4}$ ч
      Время мотоциклиста: $\frac{S}{40}$ ч
      Разница: $\frac{S}{4} - \frac{S}{40} = 4,5$
      $10S - S = 180 \Rightarrow 9S = 180 \Rightarrow S = 20$ км
      Ответ: 20.