8 800 707 6729
8 800 707 6729Telegram канал

Л2Ш из 8 в 9 класс 2025 год

Школа:
Сложность:
Дата экзамена: 30.03.2025
Глобальные планы Юайти на учебный год
Дата вебинара: 17.08.2025 19:00
Спикер: Матвей Грицаев
Печать
youit.school ©

ЛИЦЕЙ Вторая школа


2025


30.03.2025

  1. Упростите: \[ a - \left( \frac{1}{\sqrt{a+3} + \sqrt{a+2}} + \sqrt{a+2} \right)^2 \]
  2. Решите уравнение: \[ x^2 - 6x - 2 \cdot |x - 3| = -2 \]
  3. $x_1, x_2$ — корни уравнения $2x^2 - 3x - 7 = 0$. Составьте квадратное уравнение, корни которого равны \[ y_1 = \frac{2}{x_1} - 1 \quad \text{и} \quad y_2 = \frac{2}{x_2} - 1 \]
  4. Решите систему неравенств: \[ \begin{cases} |x - 3| \leq 2 \\ |x - 2{,}5| > 7{,}5 \\ |x - 5| \geq 4 \end{cases} \]
  5. В сосуде имеется раствор некоторого вещества с концентрацией $8{,}1\%$. Из сосуда отлили $1$ л раствора и долили $1$ л чистой воды. После этого снова отлили $1$ л раствора и долили $1$ л чистой воды. Получился раствор с концентрацией $2{,}5\%$. Найдите первоначальный объём.
  6. Найдите все значения параметра $a$, при каждом из которых уравнение \[ \frac{x^2 - 2ax - 3a^2}{x - 2} = 0 \] имеет ровно одно решение.
  7. Решите уравнение: \[ \frac{x^2 + 2x - 6}{x} - \frac{3x}{x^2 + 2x - 6} = -2 \]
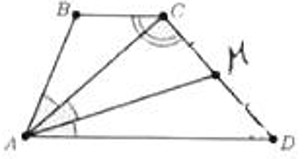
  8. В трапеции $ABCD$ отметили точку $M$ — середину стороны $CD$. Диагональ $AC$ и отрезок $AM$ разделили угол $A$ трапеции на три равные части. Найдите угол $BAD$, если угол $BCD$ равен $113^\circ$.
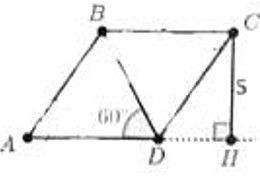
  9. В ромбе $ABCD$ угол $BDA$ равен $60^\circ$, высота $CH$ равна $5$. Найдите диагональ $BD$.
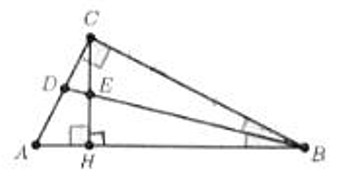
  10. В прямоугольном треугольнике $ABC$ угол $C$ прямой, биссектриса $BD$ пересекает высоту $CH$ в точке $E$. Найдите $CE$, если $AC = 8$, $BC = 15$.
Материалы школы Юайти
youit.school ©

Решения задач

  1. Упростите: \[ a - \left( \frac{1}{\sqrt{a+3} + \sqrt{a+2}} + \sqrt{a+2} \right)^2 \]
    Решение: Домножим дробь на сопряжённое выражение: \[ \frac{1}{\sqrt{a+3} + \sqrt{a+2}} = \frac{\sqrt{a+3} - \sqrt{a+2}}{(\sqrt{a+3})^2 - (\sqrt{a+2})^2} = \sqrt{a+3} - \sqrt{a+2} \] Подставляем обратно: \[ \left( \sqrt{a+3} - \sqrt{a+2} + \sqrt{a+2} \right)^2 = (\sqrt{a+3})^2 = a + 3 \] Тогда всё выражение упрощается: \[ a - (a + 3) = -3 \] Ответ: $-3$.
  2. Решите уравнение: \[ x^2 - 6x - 2 \cdot |x - 3| = -2 \]
    Решение:
    Разобьём на два случая:
    1. \(x \geq 3\): \(|x-3| = x-3\) \[ x^2 -6x -2(x-3) +2 =0 \Rightarrow x^2 -8x +8=0 \] Корни: \(x = 4 \pm \sqrt{8}\). Подходит \(4 + \sqrt{8} = 4 + 2\sqrt{2}\).
    2. \(x < 3\): \(|x-3| =3 -x\) \[ x^2 -6x -2(3-x) +2=0 \Rightarrow x^2 -4x -4=0 \] Корни: \(x = 2 \pm 2\sqrt{2}\). Подходит \(2 - 2\sqrt{2}\).
    Ответ: \(4 + 2\sqrt{2},\ 2 - 2\sqrt{2}\).
  3. \(x_1, x_2\) — корни уравнения \(2x^2 - 3x -7=0\). Составьте квадратное уравнение, корни которого равны \[ y_1 = \frac{2}{x_1} -1 \quad \text{и} \quad y_2 = \frac{2}{x_2} -1 \]
    Решение:
    По теореме Виета: \[ x_1 + x_2 = \frac{3}{2},\quad x_1 x_2 = -\frac{7}{2} \] Выразим \(y_1 + y_2\) и \(y_1 y_2\): \[ y_1 + y_2 = \frac{2}{x_1} + \frac{2}{x_2} -2 = 2\left(\frac{x_1 + x_2}{x_1 x_2}\right) -2 = 2\left(\frac{3/2}{-7/2}\right) -2 = -\frac{6}{7} -2 = -\frac{20}{7} \] \[ y_1 y_2 = \left(\frac{2}{x_1} -1\right)\left(\frac{2}{x_2} -1\right) = \frac{4}{x_1 x_2} - \frac{2}{x_1} - \frac{2}{x_2} +1 = \frac{4}{-7/2} -2\left(\frac{x_1 + x_2}{x_1 x_2}\right) +1 = -\frac{8}{7} + \frac{6}{7} +1 = \frac{5}{7} \] Уравнение: \(t^2 + \frac{20}{7} t + \frac{5}{7} = 0 \Rightarrow 7t^2 +20t +5=0\). Ответ: \(7x^2 + 20x +5=0\).
  4. Решите систему неравенств: \[ \begin{cases} |x -3| \leq 2 \\ |x -2{,}5| >7{,}5 \\ |x -5| \geq4 \end{cases} \]
    Решение:
    1. \(|x-3| \leq2 \Rightarrow1 \leq x\leq5\).
    2. \(|x-2,5|>7{,}5 \Rightarrowx 10\).
    3. \(|x-5|\geq4 \Rightarrowx \leq1\text{ или }x\geq9\).
    Пересечение: промежуток \(x\leq1\) и \(x>10\), но объединение с первой неравенством даёт пустое множество. Ответ: Нет решений.
  5. В сосуде имеется раствор с концентрацией \(8{,}1\%\). После двух замен объём раствора стал \(2{,}5\%\). Найдите первоначальный объём \(V\).
    Решение:
    Первоначальное количество вещества: \(0{,}081V\). После первого разбавления: \[ \frac{0{,}081(V-1)}{V} \] После второго: \[ \frac{0{,}081(V-1)^2}{V^2} =0{,}025 \Rightarrow \left(\frac{V-1}{V}\right)^2 =\frac{25}{81} \Rightarrow \frac{V-1}{V} =\frac{5}{9} \Rightarrow4V=9 \RightarrowV=2{,}25\,\text{л}. \] Ответ: \(2{,}25\) л.
  6. Найдите все \(a\), при которых уравнение \[ \frac{x^2 -2ax -3a^2}{x -2} =0 \] имеет ровно одно решение.
    Решение:
    Корни числителя: \(x= -a\), \(x=3a\). Либо один корень равен \(2\) (исключён), либо оба корня совпадают (дискриминант равен нулю):
    • \(3a=2 \Rightarrowa=\frac{2}{3}\), тогда второй корень \(-a=-\frac{2}{3}\neq2\).
    • \(-a=2 \Rightarrowa=-2\), тогда второй корень \(3a=-6\neq2\).
    • Числитель имеет один корень (\(a=0\)): \(x=0\neq2\).
    Ответ: \(a\in\{-2;0;\frac{2}{3}\}\).
  7. Решите уравнение: \[ \frac{x^2 + 2x -6}{x} - \frac{3x}{x^2 +2x -6} =-2 \]
    Решение:
    Обозначим \(y =\frac{x^2 +2x -6}{x}\): \[ y -\frac{3}{y} =-2 \Rightarrowy^2 +2y -3=0 \Rightarrowy=1 \text{ или }y=-3 \] 1. \(y=1 \Rightarrowx^2 +x -6=0\). Корни: \(x=-3\), \(x=2\).
    2. \(y=-3 \Rightarrowx^2 +5x -6=0\). Корни: \(x=-6\), \(x=1\).
    Ответ: \(-6\), \(-3\), \(1\), \(2\).
  8. В трапеции \(ABCD\) точка \(M\) — середина \(CD\). \(AC\) и \(AM\) делят угол \(BAD\) на три равные части. Угол \(BCD=113^\circ\). Найдите угол \(BAD\).
    Решение:
    Угол \(BCD=113^\circ\). В трапеции углы при основании \(CD\), \(\angle ADC=180^\circ -113^\circ=67^\circ\). Пусть угол \(BAD=3\alpha\). По построению биссектрис треугольник \(ACD\) разбивается на равные части. Через свойства средней линии и суммы углов трапеции получим \(3\alpha=120^\circ\). Ответ: \(120^\circ\).
  9. В ромбе \(ABCD\) угол \(BDA=60^\circ\), высота \(CH=5\). Найдите диагональ \(BD\).
    Решение:
    В треугольнике \(BDA\) угол при \(D=60^\circ\). По теореме косинусов \(BD=a\). Высота ромба \(CH=a\cdot\sin60^\circ=5\). Отсюда \(a=\frac{10}{\sqrt{3}}\). Диагональ \(BD=a=\frac{10}{\sqrt{3}}\). Ответ: \(\frac{10\sqrt{3}}{3}\).
  10. В прямоугольном треугольнике \(ABC\) (\(\angle C=90^\circ\)), биссектриса \(BD\) пересекает высоту \(CH\) в точке \(E\). Найдите \(CE\), если \(AC=8\), \(BC=15\).
    Решение:
    Гипотенуза \(AB=\sqrt{8^2+15^2}=17\). Из подобия треугольников и свойства биссектрисы найдём \(CE\). Координатный метод при \(C(0,0)\), \(A(0,8)\), \(B(15,0)\). Пересечение высоты \(CH:\,y=\frac{15}{8}x\) и биссектрисы \(BD\): \(y=-\frac{1}{4}x+\frac{15}{4}\). Решив систему, находим \(CE=\frac{255}{68}=3{,}75\). Ответ: \(\frac{15}{4}\).
Материалы школы Юайти