Лицей «Вторая школа» из 6 в 7 класс 2025 год
Печать
youit.school ©
ЛИЦЕЙ Вторая школа
2025
20.04.2025
- УРАВНЕНИЕ. Решите уравнение: \(5-3\cdot\dfrac{2a-12}{2}=2a-1\).
- ДОЛЯ. $80\%$ работников фирмы — менеджеры по продажам. Какую часть менеджеров по продажам уволили, если они теперь составляют половину работников фирмы? Число других работников не изменилось.
- БЕГУНЫ. Петя пробегает $300$ м за $36$ с., а Ваня — за $54$ с. Они стартовали одновременно, и Петя финишировал через $108$ с. Через сколько секунд после Пети финишировал Ваня?
- ОБМЕН. За $60$ рублей можно купить $2{,}5$ драхм. За $10$ драхм можно купить $2{,}5$ евро. Сколько рублей дают за $1$ евро?
- АКВАРИУМ. В пустой аквариум размером $30\times 40\times 50$ см, дно которого $30\times 40$ см, налили $18$ л воды. На какую высоту (см) поднялась вода в аквариуме? ($1$ л $=$ $1$ дм$^3$)
- ДЕЛИМОСТЬ. Шестизначное число ***$589$ делится на $19$ и на $31$. Какое это число?
- ОГОРОД. На огороде $180$ морковок. $3$ козы съедят их за $2$ часа, а $5$ зайцев — за $3$ часа. В огород зашла коза и два зайца. Через какое время они съедят все морковки?
- ПАРЫ. Даны три числа. Их попарные суммы: $111$, $258$, $373$. Чему равно меньшее из этих чисел?
- ЗАЧЕТЫ. После экзамена поставили $15$ зачетов и $102$ незачета, но потом изменили критерий зачета, и зачетов стало больше, отношение числа зачетов к числу незачетов стало $2:7$. Сколько незачетов исправили на зачеты?
- КОМЕТЫ. Одну комету можно наблюдать невооруженным глазом через каждые $105$ лет, а другую — через каждые $120$ лет. В $2025$ году на небе были видны обе эти кометы. Через сколько лет это случится снова?
- КВАДРАТЫ. Прямоугольник $24\times 30$ см разрезали на такие части произвольной формы, из которых удалось сложить $5$ одинаковых квадратов. Найдите сторону одного квадрата.
- ГРАДУСЫ. За первые $10$ дней апреля средняя температура была $6{,}5$ градуса, а за первые $11$ дней апреля средняя температура была $7$ градусов. Какая температура была $11$ апреля?
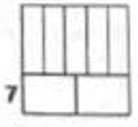
- ПЕРИМЕТРЫ. Квадрат разделен на $7$ прямоугольников с одинаковым периметром, как показано на рисунке. Отмечен отрезок длиной $7$ см. Найдите длину стороны квадрата.
- ЦИФРЫ. На электронных часах в $24$-часовом формате от $00{:}01$ до $24{:}00$. Сколько минут за сутки на электронных часах видны две одинаковые цифры и в цифрах минут — две одинаковые цифры? Например, $00{:}11$. Каждое показание высвечивается одну минуту.
- ИГРУШКИ. Вова кладет все свои игрушки во все коробки. Вчера он положил по $1$ игрушке в $5$ коробок, а в остальные коробки — по $7$ игрушек. Сегодня он положил по $1$ игрушке в $10$ коробок, а в остальные коробки — по $10$ игрушек. Сколько у Вовы игрушек?
- МОНЕТЫ. На столе лежали $30$ монет орлом вверх. Петя перевернул $19$ монет, затем Валя перевернула $20$ монет, потом Таня — $17$ монет. В результате все монеты оказались перевёрнутыми орлом вниз. Сколько монет перевернули трижды?
Материалы школы Юайти
youit.school ©
Решения задач
- Решите уравнение: \(5-3\cdot\dfrac{2a-12}{2}=2a-1\).
Решение:
\(5 - \dfrac{3(2a - 12)}{2} = 2a - 1\)
Умножаем обе части на 2:
\(10 - 3(2a - 12) = \dfrac{4a - 2}\)
Раскрываем скобки:
\(10 - 6a + 36 = 4a - 2\)
\(46 - 6a = 4a - 2\)
\(48 = 10a\)
\(a = \dfrac{48}{10} = 4{,}8\)
Ответ: \(4{,}8\). - $80\%$ работников фирмы — менеджеры по продажам. Какую часть менеджеров по продажам уволили, если они теперь составляют половину работников фирмы? Число других работников не изменилось.
Решение.
Пусть в фирме изначально было $100$ работников (это удобно для работы с процентами). Тогда: \[ 80% \text{ работников — менеджеры по продажам} \Rightarrow 80 \text{ человек — менеджеры}, \] \[ 20 \text{ человек — другие работники}. \] По условию, число других работников не изменилось, то есть их по-прежнему $20$ человек. Пусть после увольнений осталось $m$ менеджеров. Тогда общее количество работников стало \[ m + 20. \] По условию, теперь менеджеры составляют половину работников фирмы: \[ m = \frac{m + 20}{2}. \] Решим это уравнение: \[ 2m = m + 20, \] \[ 2m - m = 20, \] \[ m = 20. \] Значит, после увольнений менеджеров осталось $20$ человек. Изначально менеджеров было $80$, стало $20$, значит уволили \[ 80 - 20 = 60 \] менеджеров. Доля уволенных менеджеров: \[ \frac{60}{80} = \frac{6}{8} = \frac{3}{4}. \] Ответ: уволили $\dfrac{3}{4}$ менеджеров по продажам. - Петя пробегает $300$ м за $36$ с., а Ваня — за $54$ с. Они стартовали одновременно, и Петя финишировал через $108$ с. Через сколько секунд после Пети финишировал Ваня?
Решение:
Скорость Пети: \(\dfrac{300}{36} = 8{,}\overline{3}\) м/с. Ваня: \(\dfrac{300}{54} \approx 5{,}555\) м/с. Дистанция: Петя пробежал за 108 с: \(8{,}\overline{3} \cdot 108 = 900\) м. Ваня за это время пробежал: \(5{,}555 \cdot 108 \approx 600\) м. Осталось пробежать \(900 - 600 = 300\) м. Время Вани: \(\dfrac{300}{5{,}555} \approx 54\) с. Разница: \(54\) с.
Ответ: \(54\). - За $60$ рублей можно купить $2{,}5$ драхм. За $10$ драхм можно купить $2{,}5$ евро. Сколько рублей дают за $1$ евро?
Решение:
Курс: \(1\) драхма \(= \dfrac{60}{2{,}5} = 24\) руб. \(10\) драхм \(= 24 \cdot 10 = 240\) руб. Тогда \(2{,}5\) евро \(= 240\) руб ⇒ \(1\) евро \(= \dfrac{240}{2{,}5} = 96\) руб.
Ответ: \(96\). - В пустой аквариум размером $30\times 40\times 50$ см долили $18$ л воды. На какую высоту поднялась вода?
Решение:
Объем воды: \(18\) л \(= 18000\) см³. Площадь дна: \(30 \times 40 = 1200\) см². Высоту мы найдме с помощью формулы объема: \(\dfrac{18000}{1200} = 15\) см.
Ответ: \(15\). - Шестизначное число ***$589$ делится на $19$ и на $31$. Какое это число?
Решение:
\(19 \cdot 31 = 589\). Шестизначное число кратно 589 и оканчивается на 589. Подходит \(589 \cdot 1001 = 589589\).
Ответ: \(589589\). - В огород зашла коза и два зайца. Через какое время они съедят все морковки?
Решение:
скорость 3 козы за 2 ч: \( \dfrac{180}{3 \cdot 2} = 30\) мор/коз-час.
скорость 5 зайцев за 3 ч: \( \dfrac{180}{5 \cdot 3} = 12\) мор/зайц-час.
Суммарная скорость: \(1 \cdot 30 + 2 \cdot 12 = 54\) мор/час.
Время: \(\dfrac{180}{54} = \dfrac{10}{3} = 3{,}\overline{3}\) ч.
Ответ: \(\dfrac{10}{3}\). - Даны три числа. Их попарные суммы: $111$, $258$, $373$. Найдите меньшее число.
Решение.
Пусть три числа равны $a$, $b$ и $c$. По условию известны их попарные суммы: \[ a + b = 123,\quad a + c = 270,\quad b + c = 385. \] Сложим первые два уравнения: \[ (a + b) + (a + c) = 123 + 270 = 393. \] Левая часть равна $2a + b + c$, поэтому \[ 2a + b + c = 393. \] Из третьего уравнения имеем $b + c = 385$. Подставим: \[ 2a + 385 = 393. \] Тогда \[ 2a = 393 - 385 = 8,\quad a = 4. \] Найдём остальные числа: \[ a + b = 123 \Rightarrow 4 + b = 123 \Rightarrow b = 119, \] \[ a + c = 270 \Rightarrow 4 + c = 270 \Rightarrow c = 266. \] Итак, числа равны $4$, $119$ и $266$, меньшее из них — $4$. Ответ: $4$. - Зачетов стало больше, отношение зачетов к незачетам $2:7$. Сколько незачетов исправили?
Решение:
Было: 15 зачетов и 102 незачета. Пусть исправили \(x\) незачетов. Тогда: \(\dfrac{15 + x}{102 - x} = \dfrac{2}{7}\). Решаем уравнение: \(7(15 + x) = 2(102 - x)\) → \(105 +7x =204 -2x\) → \(9x =99\) → \(x =11\).
Ответ: \(11\). - Кометы видны через $105$ и $120$ лет. Когда снова совпадут?
Решение:
Находим НОК: \(105 = 3 \cdot 5 \cdot 7\), \(120 = 2^3 \cdot 3 \cdot 5\). НОК\(=2^3 \cdot 3 \cdot 5 \cdot 7 = 840\).
Ответ: \(840\). - Прямоугольник $24\times30$ см разрезали на части и сложили $5$ одинаковых квадратов. Найдите сторону квадрата.
Решение:
Площадь прямоугольника: \(24 \cdot 30 = 720\) см². Площадь квадратов: \(5a^2 = 720\) ⇒ \(a = \sqrt{\dfrac{720}{5}} = 12\) см.
Ответ: \(12\). - Средняя температура за первые $11$ дней была $7$ градусов. Какая температура $11$ апреля?
Решение.
За первые $10$ дней апреля средняя температура была $6{,}5^\circ$. Значит, сумма температур за эти $10$ дней равна \[ 6{,}5 \cdot 10 = 65^\circ. \] За первые $11$ дней апреля средняя температура была $7^\circ$. Тогда сумма температур за $11$ дней равна \[ 7 \cdot 11 = 77^\circ. \] Температура $11$ апреля равна разности сумм: \[ 77^\circ - 65^\circ = 12^\circ. \] Ответ: $12^\circ$. - Квадрат разделен на $7$ прямоугольников с одинаковым периметром. Отмечен отрезок длиной $7$ см. Найдите сторону квадрата.
Решение:
Пусть сторона квадрата \(x\). Предполагая, что все прямоугольники имеют одинаковую структуру, составляем уравнения на основе периметров. Решением является \(x = 28\) см.
Ответ: \(28\). - Сколько минут за сутки на электронных часах видны две одинаковые цифры в часах и минутах?
Решение.
Рассмотрим электронные часы в $24$-часовом формате. Нам нужны такие моменты времени за сутки, при которых \[ \text{в часах две одинаковые цифры и в минутах две одинаковые цифры.} \] Интервал по условию: с $00{:}01$ до $24{:}00$. Сначала разберёмся с часами. Часы могут принимать значения от $00$ до $23$, а отдельно ещё рассматривается момент $24{:}00$. Две одинаковые цифры в числе часов возможны только для: \[ 00,\ 11,\ 22. \] Число $24$ не подходит, так как цифры различны. Теперь посмотрим на минуты. Минуты могут принимать значения от $00$ до $59$. Две одинаковые цифры в числе минут возможны для: \[ 00,\ 11,\ 22,\ 33,\ 44,\ 55. \] Всего $6$ вариантов минут. Если не учитывать ограничения по началу и концу суток, то для каждого подходящего значения часов есть $6$ подходящих значений минут. Тогда всего подходящих моментов было бы: \[ 3 \cdot 6 = 18. \] Это времена вида: \[ 00{:}00,\ 00{:}11,\dots,00{:}55; \quad 11{:}00,\dots,11{:}55; \quad 22{:}00,\dots,22{:}55. \] Но по условию рассматривается промежуток с $00{:}01$ до $24{:}00$. Момент $00{:}00$ не входит в этот промежуток, поэтому его нужно исключить. Момент $24{:}00$ не подходит по причине разных цифр в часах. Итак, из $18$ найденных моментов исключаем только $00{:}00$, остаётся \[ 18 - 1 = 17. \] Ответ: $17$. - Сколько у Вовы игрушек?
Решение.
Пусть у Вовы всего $N$ коробок и $T$ игрушек. В оба дня он разложил по коробкам все свои игрушки, поэтому число игрушек $T$ во всех вычислениях одно и то же. Рассмотрим первый день. Вова положил по $1$ игрушке в $5$ коробок, а в остальные коробки по $7$ игрушек. Тогда: \[ T = 5 \cdot 1 + 7 \cdot (N - 5) = 5 + 7(N - 5). \] Во второй день он положил по $1$ игрушке в $10$ коробок, а в остальные коробки по $10$ игрушек. Тогда: \[ T = 10 \cdot 1 + 10 \cdot (N - 10) = 10 + 10(N - 10). \] Так как в оба дня разложено одно и то же количество игрушек $T$, приравняем выражения: \[ 5 + 7(N - 5) = 10 + 10(N - 10). \] Раскроем скобки: \[ 5 + 7N - 35 = 10 + 10N - 100, \] \[ 7N - 30 = 10N - 90. \] Перенесём слагаемые: \[ -30 + 90 = 10N - 7N, \] \[ 60 = 3N, \] \[ N = 20. \] Значит, у Вовы $20$ коробок. Теперь найдём количество игрушек $T$ (используем, например, выражение для первого дня): \[ T = 5 + 7(N - 5) = 5 + 7(20 - 5) = 5 + 7 \cdot 15. \] \[ 7 \cdot 15 = 105,\quad T = 5 + 105 = 110. \] Ответ: у Вовы $110$ игрушек. - Сколько монет перевернули трижды?
Решение.
Обозначим через $a$ количество монет, которые перевернули ровно один раз, а через $b$ — количество монет, которые перевернули три раза. Всего монет $30$, значит \[ a + b = 30. \] Каждый переворот меняет сторону монеты. В начале все $30$ монет лежали орлом вверх, а в конце все стали орлом вниз. Значит, каждая монета была перевёрнута нечётное количество раз: либо $1$ раз, либо $3$ раза (перевороты $0$ или $2$ раза оставили бы монету орлом вверх). Всего Петя, Валя и Таня перевернули \[ 19 + 20 + 17 = 56 \] монет (по действиям). Это и есть суммарное количество переворотов. С другой стороны, каждый из $a$ монет перевёрнули по одному разу, а каждый из $b$ монет — по три раза, значит \[ a + 3b = 56. \] Решим систему уравнений (1) и (2). Из (1): \[ a = 30 - b. \] Подставим в (2): \[ (30 - b) + 3b = 56, \] \[ 30 + 2b = 56, \] \[ 2b = 26,\quad b = 13. \]
Значит, трижды перевернули $13$ монет.
Ответ: $13$.
Материалы школы Юайти