Лицей «Вторая школа» из 6 в 7 класс 2025 год
Печать
youit.school ©
ЛИЦЕЙ Вторая школа
2025
11.04.2025
- ДРОБЬ. Числитель и знаменатель дроби — целые положительные числа. Числитель увеличили на $1$, а знаменатель — на $100$, в результате дробь увеличилась. Приведите пример такой дроби.
- ПРОЦЕНТЫ. Цену куска сыра увеличили на $80\%$, а его массу уменьшили на $10\%$. На сколько процентов увеличилась цена сыра за килограмм?
- УРАВНЕНИЕ. Решите уравнение: \[ \frac{5-2x}{2}-\frac{3-x}{3}=2x-1. \] Ответ дайте в виде обыкновенной дроби.
- НОД. Найдите наибольший общий делитель трёх чисел: НОД($2^5\cdot 3^4\cdot 5^2$; $2^4\cdot 3^3\cdot 5^3$; $2^2\cdot 3^2\cdot 5^4$).
- БАНКИ. На день рождения Винни-Пух получил от Кролика $1{,}8$ кг мёда, а от Пятачка — в $3$ раза меньше. Вес мёда был в одинаковых банках, которых Кролик дал на $8$ больше, чем Пятачок. Сколько всего банок мёда получил Пух от Кролика и Пятачка?
- СЕНО. Когда на ферме было $20$ коров, им хватало $3$ стога сена на $15$ дней. Когда на ферме стало $25$ коров, им завезли $4$ стога сена. На сколько дней хватит этого сена? Все коровы едят одинаково с постоянной скоростью.
- СЕРЕДИНА. На координатной прямой отмечены точки $A(-77)$ и $B(123)$. Найдите координату середины отрезка $AB$. (Не забудьте проверить ответ).
- СУММА. Некоторое трёхзначное число сложили с числом, записываемым теми же цифрами, но в обратном порядке, и получили $1777$. Какие числа складывали?
- ДРУЗЬЯ. В классе $27$ учеников. У всех девочек разное число друзей среди мальчиков в этом классе. Какое наибольшее число девочек может быть? (Можно ни с кем не дружить)
- КОД. В кодовом замке $3$ окошка, в каждом окошке можно выставить цифру от $0$ до $9$. Замок сломался, и теперь он открывается, если правильно выставить какие-то две цифры из трёх в соответствующих окошках. Сколько есть вариантов теперь открыть замок?
- ПОЛЯ. Тракторист, работая с постоянной скоростью, вспахал поле размерами $60$ м на $40$ м за $16$ минут. Сколько минут ему понадобится, чтобы вспахать поле размерами $70$ м на $30$ м?
- ОБЪЕМ. На картинке все бруски одинаковые. У бруска ширина равна $3$ см (отмечена на рисунке), а длина и высота неизвестны. Найдите объем одного бруска.
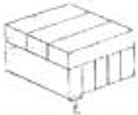
- СКОРОСТЬ. Одно и то же расстояние катер прошел по течению за $3$ часа, а против течения — за $4$ часа. Во сколько раз скорость катера больше скорости течения? Обозначьте скорость катера в стоячей воде $v$, скорость течения $u$, найдите отношение $\dfrac{v}{u}$.
- СМЕСЬ. В магазине продается смесь орехов и изюма по цене $120$ рублей за килограмм. Чистые орехи стоят $150$ рублей за килограмм, а изюм — $100$ рублей за килограмм. Сколько граммов изюма в килограмме смеси?
- КВАДРАТЫ. Квадрат составлен из квадратика и уголка. Площадь уголка равна площади центрального квадратика. Во сколько раз площадь квадрата больше площади центрального квадратика?

- КЛАССЫ. В двух классах вместе $50$ учеников. Каждый четвероклассник пожал руку четырём пятиклассникам, при этом каждый пятиклассник пожал руку шести четвероклассникам. Сколько учеников в $4$ классе?
Материалы школы Юайти
youit.school ©
Решения задач
- Вычислите без калькулятора:
\[
\Bigl(6\tfrac{7}{12} - 3\tfrac{17}{36}\Bigr)\;\cdot\;2{,}5 \;-\; 4\tfrac{1}{3}\;\cdot\;\tfrac{20}{13}.
\]
Решение: Сначала преобразуем смешанные дроби: \[ 6\tfrac{7}{12} = \frac{6 \cdot 12 + 7}{12} = \frac{79}{12}, \quad 3\tfrac{17}{36} = \frac{3 \cdot 36 + 17}{36} = \frac{125}{36}, \] \[ 4\tfrac{1}{3} = \frac{13}{3}. \] Вычислим разность: \[ \frac{79}{12} - \frac{125}{36} = \frac{237 - 125}{36} = \frac{112}{36} = \frac{28}{9}. \] Умножим на 2,5: \[ \frac{28}{9} \cdot \frac{5}{2} = \frac{140}{18} = \frac{70}{9}. \] Теперь вычислим второе произведение: \[ \frac{13}{3} \cdot \frac{20}{13} = \frac{20}{3}. \] Итоговый результат: \[ \frac{70}{9} - \frac{20}{3} = \frac{70 - 60}{9} = \frac{10}{9} = 1\tfrac{1}{9}. \] Ответ: \(1\tfrac{1}{9}\). - Определите содержание воды в зерне после просушки: изначальная масса 200 кг, 25% воды (50 кг воды, 150 кг сухого вещества). После потери 20 кг новая масса зерна: 180 кг. Новая масса воды: \(50 - 20 = 30\) кг.
Решение: \[ \text{Процент воды} = \frac{30}{180} \cdot 100% = \frac{1}{6} \cdot 100% \approx 16\tfrac{2}{3}\%. \] Ответ: \(16\tfrac{2}{3}\)\%. -
Задача.
Вычислите (без калькулятора) значение выражения при \(a = 2024\) и \(b = 2025\):
\[ \left(\frac{ab}{a^2-b^2}+\frac{b}{2b-2a}\right)\cdot \frac{a+b}{2b}. \]
Решение.
1. Упростим первую скобку:
\[ \frac{ab}{a^2-b^2}+\frac{b}{2b-2a}. \]
Разложим знаменатели:
\[ a^2-b^2 = (a-b)(a+b),\quad 2b-2a = 2(b-a) = -2(a-b). \]
Тогда
\[ \frac{ab}{a^2-b^2} = \frac{ab}{(a-b)(a+b)},\qquad \frac{b}{2b-2a} = \frac{b}{-2(a-b)} = -\frac{b}{2(a-b)}. \]
Приведём к общему знаменателю \(2(a-b)(a+b)\):
\[ \frac{ab}{(a-b)(a+b)} = \frac{2ab}{2(a-b)(a+b)},\qquad -\frac{b}{2(a-b)} = -\frac{b(a+b)}{2(a-b)(a+b)}. \]
Складываем дроби:
\[ \frac{2ab - b(a+b)}{2(a-b)(a+b)}. \]
Числитель:
\[ 2ab - b(a+b) = 2ab - ab - b^2 = ab - b^2 = b(a-b). \]
Тогда
\[ \frac{2ab - b(a+b)}{2(a-b)(a+b)} = \frac{b(a-b)}{2(a-b)(a+b)} = \frac{b}{2(a+b)}. \]
Итак, первая скобка равна \(\dfrac{b}{2(a+b)}\).
2. Подставим это в исходное выражение:
\[ \left(\frac{b}{2(a+b)}\right)\cdot\frac{a+b}{2b}. \]
Сократим \(a+b\) и \(b\):
\[ \left(\frac{b}{2(a+b)}\right)\cdot\frac{a+b}{2b} = \frac{1}{4}. \]
Получили, что выражение равно \(\dfrac14\) и не зависит от конкретных значений \(a\) и \(b\) (если знаменатель не равен нулю).
3. При \(a=2024\), \(b=2025\) значение остаётся тем же:
\[ \left(\frac{ab}{a^2-b^2}+\frac{b}{2b-2a}\right)\cdot \frac{a+b}{2b} = \frac{1}{4}. \]
Ответ.
\(\dfrac{1}{4}\). - Решите систему уравнений:
\[
\begin{cases}
4x + y - 2z = 3,\\
2x + 3y + z = 10,\\
3x - 2y + 3z = 13.
\end{cases}
\]
Решение:
Выразим \(y\) из первого уравнения: \(y = 3 - 4x + 2z\). Подставим во второе и третье:
\[
2x + 3(3 - 4x + 2z) + z = 10 \Rightarrow -10x + 7z = 1,
\]
\[
3x - 2(3 - 4x + 2z) + 3z = 13 \Rightarrow 11x - 4z = 19.
\]
Решаем систему:
\[
\begin{cases}
-10x + 7z = 1,\\
11x - 4z = 19.
\end{cases}
\]
Умножим первое уравнение на 4, второе на 7:
\[
\begin{cases}
-40x + 28z = 4,\\
77x - 28z = 133.
\end{cases}
\]
Сложим уравнения: \(37x = 137 \Rightarrow x = 3,7\). Подставим \(x\) и найдём \(z = 5,571\), затем \(y\).
Ответ: \(x = \frac{137}{37}\), \(y = \frac{26}{37}\), \(z = \frac{206}{37}\). (Числовые значения можно представить как десятичные дроби). - Масса грибов: пусть белых грибов \(x\) кг, тогда лисичек \(2x\) кг, опят \(3x + 1\) кг. Общая масса: \[ x + 2x + (3x + 1) = 7 \Rightarrow 6x + 1 = 7 \Rightarrow x = 1. \] Массы: белые – 1 кг, лисички – 2 кг, опята – 4 кг. Ответ: белые – 1 кг, лисички – 2 кг, опята – 4 кг.
-
Задача.
Первую часть пути машина проехала со скоростью \(v\), вторую часть со скоростью \(\dfrac{v}{3}\). В результате средняя скорость машины за весь путь оказалась равна \(\dfrac{v}{2}\). Во сколько раз вторая часть пути длиннее первой?
Решение.
Пусть длина первой части пути равна \(s\), тогда длина второй части равна \(ks\).
Время движения по первому участку:
\[ t_1 = \frac{s}{v}. \]
Время движения по второму участку (скорость \(\dfrac{v}{3}\)):
\[ t_2 = \frac{ks}{v/3} = \frac{3ks}{v}. \]
Общее время:
\[ t = t_1 + t_2 = \frac{s}{v} + \frac{3ks}{v} = \frac{s(1+3k)}{v}. \]
Общий путь:
\[ S = s + ks = s(1+k). \]
Средняя скорость равна отношению пути ко времени:
\[ v_{\text{ср}} = \frac{S}{t} = \frac{s(1+k)}{\,s(1+3k)/v\,} = v\cdot\frac{1+k}{1+3k}. \]
По условию \(v_{\text{ср}} = \dfrac{v}{2}\), значит
\[ v\cdot\frac{1+k}{1+3k} = \frac{v}{2}. \]
Сократим на \(v\):
\[ \frac{1+k}{1+3k} = \frac{1}{2}. \]
Перемножим «крест-накрест»:
\[ 2(1+k) = 1+3k. \]
Раскрываем скобки и переносим члены:
\[ 2 + 2k = 1 + 3k \Rightarrow 2-1 = 3k-2k \Rightarrow 1 = k. \]
Значит, \(k = 1\), то есть вторая часть пути равна первой по длине.
Ответ.
Вторая часть пути в \(1\) раз длиннее первой, то есть их длины одинаковы. - Пусть скорость автомобиля \(v\), пешехода \(u\), расстояние \(S\). Время встречи: \(\frac{S}{v + u}\). За это время автомобиль проезжает \(\frac{vS}{v + u}\), пешеход проходит \(\frac{uS}{v + u}\). Время движения автомобиля после встречи: \(\frac{\frac{uS}{v + u}}{v}\)(до А) + \(\frac{S}{v}\) (обратно). Общее время: \[ \frac{S}{v + u} + \frac{uS}{v(v + u)} + \frac{S}{v} = \frac{8}{3}. \] Так как автомобиль проезжает \(S\) за 1 час (\(v = S\)): \[ \frac{1}{1 + u/S} + \frac{u/S}{(1 + u/S)} + 1 = \frac{8}{3} \Rightarrow \text{решение даёт } u/S = \frac{1}{5}. \] Время пешехода: \(S / u = 5\) часов. Ответ: 5 часов.
Материалы школы Юайти