Л2Ш из 6 в 7 класс 2025 год

ЛИЦЕЙ Вторая школа

2025

03.06.2025

1. ЯЩИКИ. В двух ящиках $126$ кг песка. Если из первого пересыпать одну восьмую лежащего там песка во второй, то песка в ящиках станет поровну. Сколько кг песка было в первом ящике?
2. ПАРЫ. Даны три числа. Если сложить все пары чисел, то получатся суммы: $121$, $268$, $383$. Чему равно меньшее из этих чисел?
3. АКВАРИУМ. В пустой аквариум размером $30\times 40\times 50$ см, дно которого $30\times 40$ см, налили $18$ л воды. На какую высоту (см) поднялась вода в аквариуме? ($1$ л $=$ $1$ дм$^3$)
4. ВЕСЫ. Антоше подарили весы, и он стал взвешивать всё подряд. Вес самолета (С) оказался равным сумме мяча (М) и двух кубиков (К), а вес самолета и кубика — весу двух мячей. Сколько кубиков уравновесит самолет?
5. СЕНО. Когда на ферме было $20$ коров, им хватало $3$ стога сена на $15$ дней. Когда на ферме стало $25$ коров, им завезли $4$ стога сена. На сколько дней хватит этого сена? Все коровы едят одинаково с постоянной скоростью.
6. БЕТОН. Бетонная смесь состоит из песка, глины и гипса. Если массу смеси разделить на равные части, то песок составит $5$ частей, глина – $8$ частей, гипс – $2$ части. При изготовлении смеси в нее положили глины на $30$ кг больше, чем песка. Сколько килограммов весит вся смесь?
7. КВАДРАТИКИ. Картонный квадрат со стороной $3$ м разрезали на квадратики со стороной $5$ см и положили их подряд в один ряд. Найдите длину полученного ряда в метрах.
8. КОМЕТЫ. Одну комету можно наблюдать невооруженным глазом через каждые $105$ лет, а другую — через каждые $120$ лет. В $2025$ году на небе были видны обе эти кометы. Через сколько лет это случится снова?
9. ДРУЗЬЯ. В классе $27$ учеников. У всех девочек разное число друзей среди мальчиков в этом классе. Какое наибольшее число девочек может быть? (Можно ни с кем не дружить)
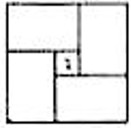
10. КВАДРАТЫ. Квадрат составлен из квадратика в центре и четырех равных прямоугольников. Сторона квадрата $101$ см, сторона квадратика $1$ см. Найдите стороны одного прямоугольника.
    
11. МЯЧ. Мяч стоит $5600$ руб. Петя и Ваня договорились заплатить за него поровну, но у Пети было на руках только $2000$ руб., поэтому Ваня внес $3600$ руб. Ранее Петя давал Ване в долг $1000$ руб. Сколько следует Ване отдать денег Пете, чтобы никто никому не был должен?
12. РЫЦАРИ. За круглым столом сидят $45$ человек, рыцарей и лжецов, и не все они лжецы. Каждый произнёс фразу: «Мои двое соседей (слева и справа) разные — $1$ рыцарь и $1$ лжец». Сколько рыцарей за столом? Рыцари говорят правду, лжецы лгут.
13. ПЕРИМЕТРЫ. Прямоугольник разделен двумя прямыми на $4$ прямоугольника. Известны периметры трех маленьких прямоугольников: $8$, $12$, $17$. Найдите периметр четвертого, который напротив прямоугольника с периметром $17$ (стороны бывают дробными).
    
14. ОГОРОД. На огороде $180$ морковок. $3$ козы съедят их за $2$ часа, а $5$ зайцев — за $3$ часа. В огород зашла коза и два зайца. Через сколько минут они съедят все морковки?
15. РУЧКИ. В классе у каждого есть ручка. Ровно у $10$ детей есть хотя бы $1$ ручка, ровно у $8$ детей — хотя бы $2$ ручки, ровно у $6$ детей — хотя бы $3$ ручки, ровно у $4$ детей — хотя бы $4$ ручки, и ровно у $2$ детей — ровно $5$ ручек. Ни у кого нет больше $5$ ручек. Сколько ручек у всех детей вместе?
16. МИЛИ. Гендальф сказал Фродо, что перевести эльфийские мили в человеческие нужно так: разделить расстояние в эльфийских милях на $5$ и полученное число уменьшить на $5\%$. Фродо прошел $200$ эльфийских миль. Сколько это человеческих миль?

Решения задач

1. ЯЩИКИ. В двух ящиках $126$ кг песка. Если из первого пересыпать одну восьмую лежащего там песка во второй, то песка в ящиках станет поровну. Сколько кг песка было в первом ящике?
   Решение: Пусть в первом ящике $x$ кг. После пересыпания:
   $\frac{7x}{8} = 126 - x + \frac{x}{8} \Rightarrow 7x = 1008 - 8x + x \Rightarrow 14x = 1008 \Rightarrow x = 72$
   Ответ: 72 кг.
2. ПАРЫ. Даны три числа. Если сложить все пары чисел, то получатся суммы: $121$, $268$, $383$. Чему равно меньшее из этих чисел?
   Решение: Обозначим числа как $a \leq b \leq c$. Тогда $a + b = 121$, $a + c = 268$, $b + c = 383$. Сложим уравнения: $2(a + b + c) = 772 \Rightarrow a + b + c = 386$. Из $a + b = 121$ находим $c = 265$, далее $a = 268 - 265 = 3$.
   Ответ: 3.
3. АКВАРИУМ. В пустой аквариум размером $30\times 40\times 50$ см, дно которого $30\times 40$ см, налили $18$ л воды. На какую высоту (см) поднялась вода в аквариуме? ($1$ л $=$ $1$ дм$^3$)
   Решение: Объем воды $18000$ см$^3$. Площадь дна $1200$ см$^2$. Высота: $\frac{18000}{1200} = 15$ см.
   Ответ: 15.
4. ВЕСЫ. Антоше подарили весы, и он стал взвешивать всё подряд. Вес самолета (С) оказался равным сумме мяча (М) и двух кубиков (К), а вес самолета и кубика — весу двух мячей. Сколько кубиков уравновесит самолет?
   Из условий:
   $C = M + 2K$ и $C + K = 2M$.
   Подставляя $C$ из первого уравнения во второе:
   $M + 3K = 2M \Rightarrow M = 3K$.
   Тогда $C = 3K + 2K = 5K$.
   Ответ: 5.
5. СЕНО. Когда на ферме было $20$ коров, им хватало $3$ стога сена на $15$ дней. Когда на ферме стало $25$ коров, им завезли $4$ стога сена. На сколько дней хватит этого сена? Все коровы едят одинаково с постоянной скоростью.
   Решение:
   Дано: \(20\) коров съедают \(3\) стога за \(15\) дней. Количество короводней в трёх стогах: \[ 20 \cdot 15 = 300. \] Один стог содержит: \[ \frac{300}{3} = 100 \text{ короводней}. \] Четыре стога содержат: \[ 4 \cdot 100 = 400 \text{ короводней}. \] Пусть корм хватит на \(x\) дней при \(25\) коровах. Тогда: \[ 25x = 400. \] Отсюда: \[ x = \frac{400}{25} = 16. \] Ответ: 16
6. БЕТОН. Бетонная смесь состоит из песка, глины и гипса. Если массу смеси разделить на равные части, то песок составит $5$ частей, глина – $8$ частей, гипс – $2$ части. При изготовлении смеси в нее положили глины на $30$ кг больше, чем песка. Сколько килограммов весит вся смесь?
   Решение:
   Разница пропорций глины и песка: \( 8 - 5 = 3 \) части. 3 части = 30 кг ⇒ 1 часть = 10 кг. Вес смеси: \[ (5 + 8 + 2) \times 10 = 150\ \text{кг}. \] Ответ: 150 кг.
7. КВАДРАТИКИ. Картонный квадрат со стороной $3$ м разрезали на квадратики со стороной $5$ см и положили их подряд в один ряд. Найдите длину полученного ряда в метрах.
   Решение: Количество квадратиков: $\left(\frac{300}{5}\right)^2 = 3600$. Длина ряда: $3600 \cdot 5 = 18000$ см = 180 м.
   Ответ: 180 м.
8. КОМЕТЫ. Одну комету можно наблюдать невооруженным глазом через каждые $105$ лет, а другую — через каждые $120$ лет. В $2025$ году на небе были видны обе эти кометы. Через сколько лет это случится снова?
   Решение: НОК$(105, 120) = 840$.
   Ответ: 840.
9. ДРУЗЬЯ. В классе $27$ учеников. У всех девочек разное число друзей среди мальчиков в этом классе. Какое наибольшее число девочек может быть? (Можно ни с кем не дружить)
   Решение:В классе \(27\) учеников. Пусть девочек \(g\), мальчиков \(b\). Тогда \[ g + b = 27. \] Каждая девочка может иметь от \(0\) до \(b\) друзей среди мальчиков. Это всего \(b+1\) разных вариантов. По условию у всех девочек число друзей разное, значит \[ g \le b + 1. \] Подставим \(b = 27 - g\): \[ g \le 28 - g, \] \[ 2g \le 28, \] \[ g \le 14. \] Ответ: 14.
10. КВАДРАТЫ. Квадрат составлен из квадратика в центре и четырех равных прямоугольников. Сторона квадрата $101$ см, сторона квадратика $1$ см. Найдите стороны одного прямоугольника.
    Решение:Квадрат со стороной \(101\) см составлен из маленького квадратика со стороной \(1\) см в центре и четырёх одинаковых прямоугольников. Тогда площади всех фигур вместе равны площади большого квадрата. Площадь большого квадрата: \[ 101 \cdot 101 = 10201. \] Площадь маленького квадратика: \[ 1 \cdot 1 = 1. \] Остальную площадь занимают четыре одинаковых прямоугольника: \[ 10201 - 1 = 10200. \] Площадь одного прямоугольника: \[ \frac{10200}{4} = 2550. \] Пусть стороны прямоугольника равны \(a\) и \(b\). Тогда \[ a \cdot b = 2550. \] Теперь подбираем такие два числа, чтобы при умножении получилось \(2550\). Заметим, что \[ 50 \cdot 50 = 2500, \quad 50 \cdot 51 = 2550. \] Подходит пара чисел \(50\) и \(51\). Значит, стороны прямоугольника: \[ 50 \text{ см и } 51 \text{ см}. \] Ответ: прямоугольник имеет стороны \(50\) см и \(51\) см.
11. МЯЧ. Мяч стоит $5600$ руб. Петя и Ваня договорились заплатить за него поровну, но у Пети было на руках только $2000$ руб., поэтому Ваня внес $3600$ руб. Ранее Петя давал Ване в долг $1000$ руб. Сколько следует Ване отдать денег Пете, чтобы никто никому не был должен?
    Решение: Переплата Вани: $3600 - 2800 = 800$ руб. Петя должен Ване $800$ руб. Но из-за долга в $1000$ руб, Ваня должен Пете $1000$ руб. Итог: $1000 - 800 = 200$ руб должен отдать Ваня.
    Ответ: 200.
12. РЫЦАРИ. За круглым столом сидят $45$ человек, рыцарей и лжецов, и не все они лжецы. Каждый произнёс фразу: «Мои двое соседей (слева и справа) разные — $1$ рыцарь и $1$ лжец». Сколько рыцарей за столом? Рыцари говорят правду, лжецы лгут.
    Решение:
    Каждый сказал: «Мои соседи — разные: один рыцарь, другой лжец.»
    
    Если это сказал рыцарь, то это правда, значит у него один сосед рыцарь, а другой лжец. Если это сказал лжец, то это ложь, значит у него оба соседа одинаковые.
    Попробуем начать с кусочка:
    Рыцарь, Рыцарь, Лжец
    Если продолжать по этому правилу, всё повторяется каждые три человека:
    (Р,\ Р,\ Л),\ (Р,\ Р,\ Л),\ (Р,\ Р,\ Л),...
    В каждом наборе из трёх человек два рыцаря и один лжец. Всего сидит \(45\) человек, а \(45\) делится на \(3\): \[ 45 \div 3 = 15 \] Значит таких троек \(15\), а рыцарей в каждой тройке \(2\): \[ 15 \times 2 = 30 \] Ответ: 30 рыцарей
13. ПЕРИМЕТРЫ. Прямоугольник разделен двумя прямыми на $4$ прямоугольника. Известны периметры трех маленьких прямоугольников: $8$, $12$, $17$. Найдите периметр четвертого, который напротив прямоугольника с периметром $17$ (стороны бывают дробными).
    Решение:
    Пусть вертикальная прямая делит большой прямоугольник на части шириной \(a\) и \(b\), а горизонтальная прямая делит его на высоты \(c\) и \(d\). Тогда периметры четырёх маленьких прямоугольников равны: сверху слева: \(2(a+c)\), сверху справа: \(2(b+c)\), снизу слева: \(2(a+d)\), снизу справа: \(2(b+d)\). Пусть периметр \(17\) относится к прямоугольнику с периметром \(2(a+c)\). Тогда периметр прямоугольника, расположенного напротив него, равен \(2(b+d)\). Оставшиеся два периметра \(8\) и \(12\) относятся к прямоугольникам с периметрами \(2(b+c)\) и \(2(a+d)\) (в каком-то порядке). Сложим периметры прямоугольников, соседних с прямоугольником с периметром \(17\): \[ 2(b+c) + 2(a+d). \] Вычтем из этой суммы периметр прямоугольника с периметром \(17\): \[ [2(b+c) + 2(a+d)] - 2(a+c) = 2(b+d). \] Но \(2(b+d)\) — это периметр прямоугольника, расположенного напротив прямоугольника с периметром \(17\). Следовательно, периметр искомого прямоугольника равен \[ 8 + 12 - 17 = 3. \] Ответ: \(3\).
14. ОГОРОД. На огороде $180$ морковок. $3$ козы съедят их за $2$ часа, а $5$ зайцев — за $3$ часа. В огород зашла коза и два зайца. Через сколько минут они съедят все морковки?
    Решение: Скорость козы $180 : 3 :2 = 30$ морк/час, зайца $180 : 5: 3 = 12$ морк/час. Совместная скорость: $30 + 2 \cdot 12 = 54$ морк/час. Время: $\frac{180}{54} \cdot 60 = 200$ минут.
    Ответ: 200.
15. РУЧКИ. В классе у каждого есть ручка. Ровно у $10$ детей есть хотя бы $1$ ручка, ровно у $8$ детей — хотя бы $2$ ручки, ровно у $6$ детей — хотя бы $3$ ручки, ровно у $4$ детей — хотя бы $4$ ручки, и ровно у $2$ детей — ровно $5$ ручек. Ни у кого нет больше $5$ ручек. Сколько ручек у всех детей вместе?
    Решение.
    Найдём, сколько детей имеют ровно столько ручек. Ровно $5$ ручек — у $2$ детей. «Не меньше $4$» — у $4$ детей, значит ровно $4$ ручки — ещё у \[ 4 - 2 = 2 \] детей. «Не меньше $3$» — у $6$ детей, значит ровно $3$ ручки — ещё у \[ 6 - 4 = 2 \] детей. «Не меньше $2$» — у $8$ детей, значит ровно $2$ ручки — ещё у \[ 8 - 6 = 2 \] детей. «Не меньше $1$» — у $10$ детей, значит ровно $1$ ручка — ещё у \[ 10 - 8 = 2 \] детей. Итак, имеем: \[ 2 \text{ ребёнка по } 1 \text{ ручке}, \quad 2 \text{ ребёнка по } 2 \text{ ручки}, \quad 2 \text{ ребёнка по } 3 \text{ ручки}, \quad 2 \text{ ребёнка по } 4 \text{ ручки}, \quad 2 \text{ ребёнка по } 5 \text{ ручек}. \] Считаем общее количество ручек: \[ 2\cdot1 + 2\cdot2 + 2\cdot3 + 2\cdot4 + 2\cdot5 = 2(1+2+3+4+5) = 2\cdot15 = 30. \] Ответ: $30$ ручек.
16. МИЛИ. Гендальф сказал Фродо, что перевести эльфийские мили в человеческие нужно так: разделить расстояние в эльфийских милях на $5$ и полученное число уменьшить на $5\%$. Фродо прошел $200$ эльфийских миль. Сколько это человеческих миль?
    Решение: $\frac{200}{5} \cdot 0.95 = 38$.
    Ответ: 38.