Л2Ш из 5 в 6 класс 2025 год

ЛИЦЕЙ Вторая школа

2025

30.03.2025

1. Половина класса – любители физики, а другая половина – математики. Когда $4$ любителей физики перешли в любители математики, то любителей математики стало вдвое больше, чем любителей физики. Сколько учеников в этом классе?
2. Из цифр $0$, $1$, $2$, $3$, $4$, $5$, $6$, $7$ составьте одно пятизначное число и одно трёхзначное так, чтобы сумма этих чисел была наибольшая. Каждую цифру надо использовать ровно один раз в одном из чисел. (Не торопитесь, — легко ошибиться)
3. Числитель и знаменатель дроби — целые положительные числа. Числитель увеличили на $1$, а знаменатель — на $100$, в результате дробь увеличилась. Приведите пример такой дроби.
4. Найдите наибольший общий делитель чисел: $1296$ и $864$.
5. Бетонная смесь состоит из песка, глины и гипса. В пропорции по массе песок составляет $5$ частей, глина – $8$ частей, гипс – $2$ части. При изготовлении смеси в нее положили глины на $30$ кг больше, чем песка. Сколько килограммов весит вся смесь?
6. Когда на ферме было $20$ коров, им хватало $3$ стога сена на $15$ дней. Когда на ферме стало $25$ коров, им завезли $4$ стога сена. На сколько дней хватит этого сена? Все коровы едят одинаково с постоянной скоростью.
7. На координатной прямой отмечены точки $A(7)$ и $B(127)$. Найдите координату середины отрезка $AB$. (Не забудьте проверить ответ).
8. Некоторое трёхзначное число сложили с числом, записанным теми же цифрами, но в обратном порядке, и получили $1777$. Какие числа складывали?
9. В классе $27$ учеников. У всех девочек разное число друзей среди мальчиков в этом классе. Какое наибольшее число девочек может быть? (Можно ни с кем не дружить)
10. В кодовом замке $3$ окошка, в каждом окошке можно выставить цифру от $0$ до $9$. Замок сломался, и теперь он открывается, если правильно выставить какие-то две цифры из трёх в соответствующих окошках. Сколько всего кодов откроет замок?
11. Тракторист, работая с постоянной скоростью, вспахал поле размерами $60$ м на $40$ м за $16$ минут. Сколько минут ему понадобится, чтобы вспахать поле размерами $70$ м на $30$ м?
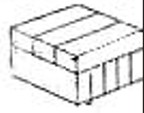
12. На картинке все бруски одинаковые. У бруска ширина равна $3$ см (отмечена на рисунке), а длина и высота неизвестны. Найдите объём одного бруска.
    
13. Оцените высоту эскалатора по следующим данным. Если мы стоим на эскалаторе, то спуск занимает $3$ мин., а если мы идём по ходу эскалатора, то спуск занимает $2$ мин., и мы проходим $70$ ступенек. Высоту всех ступенек считайте $20$ см.
14. В магазине продаётся смесь орехов и изюма по цене $120$ рублей за килограмм. Чистые орехи стоят $150$ рублей за килограмм, а изюм — $100$ рублей за килограмм. Сколько граммов изюма в килограмме смеси?
15. Квадрат составлен из квадратика в центре и четырёх равных прямоугольников. Сторона квадрата $101$ см, сторона квадратика $1$ см. Найдите стороны одного прямоугольника.
    
16. В двух классах вместе $50$ учеников. Каждый четвероклассник пожал руку четырём пятиклассникам, при этом каждый пятиклассник пожал руку шести четвероклассникам. Сколько учеников в $4$ классе?

Решения задач

1. Решение: Пусть в классе \( x \) учеников. Изначально любителей физики и математики по \( \frac{x}{2} \). После перехода 4 человек: \[ \frac{x}{2} - 4 \text{ (физиков)}, \quad \frac{x}{2} + 4 \text{ (математиков)} \] По условию математиков стало вдвое больше: \[ \frac{x}{2} + 4 = 2 \left( \frac{x}{2} - 4 \right) \Rightarrow x = 24. \] Ответ: 24.
2. Решение: Нужно составить одно пятизначное число и одно трёхзначное число из цифр \(0,1,2,3,4,5,6,7\), используя каждую цифру ровно один раз. Самые большие разряды дают наибольший вклад в сумму: \(10000, 1000, 100, 100, 10, 10, 1, 1\). Поэтому самые большие цифры \(7,6,5,4,3,2,1,0\) надо распределить по убыванию разрядов. Получается размещение: \[ 10000 \rightarrow 7,\quad 1000 \rightarrow 6,\quad 100 \rightarrow 5,\quad 100 \rightarrow 4,\quad 10 \rightarrow 3,\quad 10 \rightarrow 2,\quad 1 \rightarrow 1,\quad 1 \rightarrow 0. \] Тогда пятизначное число: \[ 76531 \] Трёхзначное число: \[ 420 \] Сумма: \[ 76531 + 420 = 76951. \] Ответ: 76951 и 420
3. Решение: Пример дроби \( \frac{1}{200} \). После изменений: \[ \frac{2}{300} > \frac{1}{200} \quad (\approx 0,0066 > 0,005). \] Дробь 1/100 не подходит так, как если увеличивать числа, то дроби получатся равными. А следующее ближайшее число 1/200 Ответ: \( \frac{1}{201} \).
4. Решение: Найдём НОД(1296, 864): \[ 1296 = 864 \times 1 + 432, \quad 864 = 432 \times 2 + 0 \Rightarrow \text{НОД} = 432. \] Ответ: 432.
5. Решение: Разница пропорций глины и песка: \( 8 - 5 = 3 \) части. 3 части = 30 кг ⇒ 1 часть = 10 кг. Вес смеси: \[ (5 + 8 + 2) \times 10 = 150\ \text{кг}. \] Ответ: 150 кг.
6. Решение: Дано: \(20\) коров съедают \(3\) стога за \(15\) дней. Количество короводней в трёх стогах: \[ 20 \cdot 15 = 300. \] Один стог содержит: \[ \frac{300}{3} = 100 \text{ короводней}. \] Четыре стога содержат: \[ 4 \cdot 100 = 400 \text{ короводней}. \] Пусть корм хватит на \(x\) дней при \(25\) коровах. Тогда: \[ 25x = 400. \] Отсюда: \[ x = \frac{400}{25} = 16. \] Ответ: 16
7. Даны точки \(A(7)\) и \(B(127)\). Чтобы найти середину отрезка, нужно сложить координаты концов и разделить на \(2\): \[ \frac{7 + 127}{2}. \] Сначала складываем: \[ 7 + 127 = 134. \] Теперь делим на \(2\): \[ \frac{134}{2} = 67. \] Ответ: 67.
8. Решение: Рассмотрим задачу. Некоторое трёхзначное число сложили с числом, записанным теми же цифрами в обратном порядке, и получили число \(1777\). Нужно найти, какие это были числа. Пусть исходное число имеет вид \(abc\), тогда число с цифрами в обратном порядке имеет вид \(cba\). Заметим, что последняя цифра суммы равна \(7\). Последние цифры слагаемых равны \(c\) и \(a\), значит \[ a + c \text{ оканчивается цифрой } 7. \] Подходящая большая сумма для двух цифр: \[ 8 + 9 = 17. \] Значит, цифры \(a\) и \(c\) равны \(8\) и \(9\) (в каком-то порядке). Теперь подберём среднюю цифру \(b\). Попробуем взять числа \(839\) и \(938\) и сложить их столбиком: \[ 839 + 938 = 1777. \] Сложение: \[ \begin{array}{r} 839 \\ +\,938 \\ \hline 1777 \end{array} \] Получилось ровно число \(1777\), значит наша догадка верна. Ответ: складывали числа \(839\) и \(938\).
9. В классе \(27\) учеников. Пусть девочек \(g\), мальчиков \(b\). Тогда \[ g + b = 27. \] Каждая девочка может иметь от \(0\) до \(b\) друзей среди мальчиков. Это всего \(b+1\) разных вариантов. По условию у всех девочек число друзей разное, значит \[ g \le b + 1. \] Подставим \(b = 27 - g\): \[ g \le 28 - g, \] \[ 2g \le 28, \] \[ g \le 14. \] Ответ: 14.
10. Пусть правильный код имеет три цифры. Замок открывается, если совпадают две или три цифры. Число кодов, где ровно две цифры стоят правильно: \[ 3 \cdot 9 = 27. \] (выбираем одну неверную позицию и ставим туда любую из девяти неправильных цифр). Кодов, где совпадают все три цифры: \[ 1. \] Общее количество: \[ 27 + 1 = 28. \] Ответ: 28.
11. Площадь первого поля: \[ 60 \cdot 40 = 2400. \] Эта площадь вспахана за \(16\) минут, значит скорость работы: \[ \frac{2400}{16} = 150. \] Площадь второго поля: \[ 70 \cdot 30 = 2100. \] Время на вспашку: \[ \frac{2100}{150} = 14. \] Ответ: 14.
12. Решение: Дано, что все бруски одинаковые, и ширина одного бруска равна \(3\) см. По рисунку видно следующее:
    • брусков по длине \(4\),
    • брусков по глубине \(2\),
    • брусков по высоте \(2\).
    Значит, размеры всей сложенной фигуры выражаются через размеры одного бруска. Ширина одного бруска равна \(3\) см, поэтому: \[ \text{глубина всей стопки} = 2 \cdot 3 = 6 \text{ см}, \] \[ \text{длина всей стопки} = 4 \cdot 3 = 12 \text{ см}. \] Так как высота стопки состоит из двух одинаковых брусков, а по рисунку видно, что высота примерно равна глубине, то можно сделать вывод, что высота одного бруска также равна его ширине: \[ h = 3 \text{ см}. \] Теперь найдём объём одного бруска. Все его три измерения равны \(3\) см: \[ V = 3 \cdot 3 \cdot 3 = 27 \text{ см}^3. \] Ответ: 27 $\text{ см}^3.$
13. Решение: Пусть длина эскалатора в ступеньках равна \(N\). Если стоять на эскалаторе, спуск занимает \(3\) минуты. Значит, за \(3\) минуты эскалатор прокручивает всю свою длину. Если идти по эскалатору, спуск занимает \(2\) минуты, и человек проходит \(70\) ступенек. За эти же \(2\) минуты эскалатор прокручивает только часть своей длины: \[ \frac{2}{3}N. \] Тогда сумма пройденного шагами и движения эскалатора должна давать всю длину эскалатора: \[ \frac{2}{3}N + 70 = N. \] Вычитаем \(\frac{2}{3}N\): \[ 70 = \frac{1}{3}N \Rightarrow N = 210. \] Всего \(210\) ступенек. Высота каждой ступеньки \(20\) см, значит высота эскалатора: \[ 210 \cdot 20 = 4200 \text{ см} = 42 \text{ м}. \] Ответ: \[ 42 \text{ метра}. \]
14. Решение: Пусть в $1$ килограмме смеси орехов и изюма орехов $x$ килограммов, а изюма $y$ килограммов. Тогда: \[ x + y = 1 \] Цена орехов $150$ рублей за килограмм, изюма $100$ рублей за килограмм, смесь стоит $120$ рублей за килограмм. Составим уравнение по цене: \[ 150x + 100y = 120 \] Подставим $y = 1 - x$: \[ 150x + 100(1 - x) = 120 \] \[ 150x + 100 - 100x = 120 \] \[ 50x + 100 = 120 \] \[ 50x = 20 \Rightarrow x = \frac{20}{50} = 0{,}4 \] Тогда: \[ y = 1 - 0{,}4 = 0{,}6 \] Изюма $0{,}6$ килограмма, то есть $600$ граммов. Ответ: $600$ граммов изюма.
15. Решение: Квадрат со стороной \(101\) см составлен из маленького квадратика со стороной \(1\) см в центре и четырёх одинаковых прямоугольников. Тогда площади всех фигур вместе равны площади большого квадрата. Площадь большого квадрата: \[ 101 \cdot 101 = 10201. \] Площадь маленького квадратика: \[ 1 \cdot 1 = 1. \] Остальную площадь занимают четыре одинаковых прямоугольника: \[ 10201 - 1 = 10200. \] Площадь одного прямоугольника: \[ \frac{10200}{4} = 2550. \] Пусть стороны прямоугольника равны \(a\) и \(b\). Тогда \[ a \cdot b = 2550. \] Теперь подбираем такие два числа, чтобы при умножении получилось \(2550\). Заметим, что \[ 50 \cdot 50 = 2500, \quad 50 \cdot 51 = 2550. \] Подходит пара чисел \(50\) и \(51\). Значит, стороны прямоугольника: \[ 50 \text{ см и } 51 \text{ см}. \] Ответ: прямоугольник имеет стороны \(50\) см и \(51\) см.
16. Решение:В двух классах всего \(50\) учеников. Пусть в \(4\) классе \(x\) человек, тогда в \(5\) классе \[ 50 - x \] человек. Каждый четвероклассник пожал руку \(4\) пятиклассникам. Всего рукопожатий со стороны четвероклассников: \[ 4x. \] Каждый пятиклассник пожал руку \(6\) четвероклассникам. Всего рукопожатий со стороны пятиклассников: \[ 6(50 - x). \] Это одни и те же рукопожатия, только посчитанные по-разному, значит: \[ 4x = 6(50 - x). \] Решим уравнение: \[ 4x = 300 - 6x, \] \[ 4x + 6x = 300, \] \[ 10x = 300, \] \[ x = 30. \] Значит, в \(4\) классе \(30\) учеников, а в \(5\) классе \[ 50 - 30 = 20. \] Ответ: в \(4\) классе \(30\) учеников.