8 800 707 6729
8 800 707 6729Telegram канал

Интеллектуал из 4 в 5 класс 2020 год вариант 2

Сложность:
Дата экзамена: 2020
Печать
youit.school ©
Поступление в Школу "Интеллектуал"
Вариант вступительного экзамена в 5 класс (по выбору). 2020 год
Математика базовая. Баллы: все задачи по 4 балла. В задачах 1--4 бинарное оценивание (0/4), в задаче 5 по 1 баллу за каждую верную пару «условие--выражение».


  1. В данном примере расставьте скобки так, чтобы результат вычислений был наибольшим из возможных: $10:11-1\cdot6$. Запишите результат.


  2. Для покраски поверхности площадью 1 дм$^2$ требуется 40 граммов краски. У Пети есть прямоугольный брусок длиной 20 см, шириной 15 см и высотой 10 см. Сколько граммов краски понадобится Пете, чтобы покрасить брусок со всех сторон?


  3. Две ватрушки и плюшка вместе стоят 130 рублей. Две ватрушки и три плюшки вместе стоят 210 рублей. Сколько стоят вместе две плюшки и ватрушка?


  4. Незнайка и Шпунтик выехали из Цветочного города в Солнечный одновременно. Незнайка ехал на автобусе со скоростью 48 км/ч, а Шпунтик на своём автомобиле со скоростью 72 км/ч. Через 4 часа мотор у Шпунтика заглох, пришлось остановиться и чинить его. Автобус с Незнайкой ехал без остановок. Когда Шпунтик починил мотор, он поехал дальше и ещё через 2 часа догнал автобус. Сколько часов потратил Шпунтик на починку мотора?


  5. Сопоставьте условие каждой задачи с числовым выражением, составленным для её решения.





Математика по выбору

  1. Галя обнаружила, что сумма точек на противоположных гранях игрального кубика всегда равна семи. Она взяла четыре одинаковых игральных кубика и склеила их, приложив друг к другу одинаковыми гранями. После этого Галя некоторые грани закрасила белой краской. Сколько точек было на грани, отмеченной «звёздочкой»?

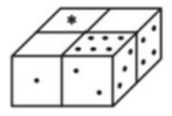
    (A) 1 (Б) 2 (В) 3 (Г) 5 (Д) нельзя определить


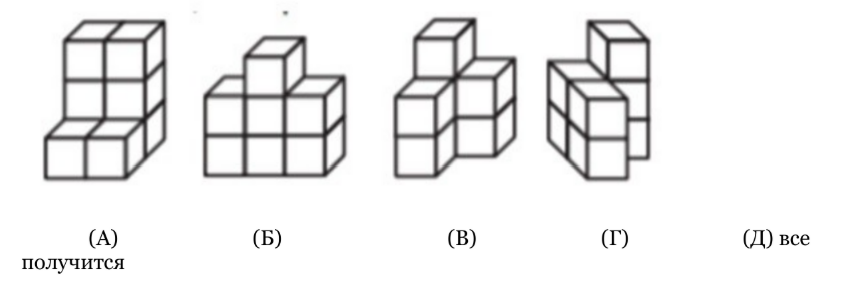
  2. На рисунках А, Б, В, Г все детали состоят из семи кубиков. Какую из этих деталей не получится составить из кусочков, нарисованных в рамочке?



  3. Попугаи Кеша, Бася и Гоша очень любят орехи. Гоше дали 6 орехов, а Кеше и Басье по 12 таких же орехов. Кеша ест в два раза быстрее, чем Бася. Гоша ест в два раза медленнее, чем Бася. Грызть орехи все попугаи начали одновременно. Кеша съел свою порцию за три минуты, после чего они с Басей вдвоём доели порцию Баси. Через сколько минут после этого Гоша доел свои орехи?


  4. Пятиклассницы записали в серые клетки на рисунке какие-то числа. Затем заполнили белые клетки, составив для этих чисел таблицу умножения. После этого несколько чисел стёрли, а несколько — заменили буквами. Какие две из букв заменяют одно и то же число?

    (A) И и К; (Б) Л и Ы; (В) К и О; (Г) Ы и Н; (Д) Ш и Ц


  5. Гномы Торин, Балин и Двалин соревновались в беге на 300 метров. Они начали бег одновременно. Каждый из них бежал с постоянной скоростью. Когда Торин финишировал, Двалин до конца дистанции оставалось 100 метров, а Балин был на 40~м впереди Двалина. Когда Балин финишировал, то на каком расстоянии до конца дистанции был Двалин?
    (A) 20 м (Б) 30 м (В) 40 м (Г) 50 м (Д) 60 м


  6. Незнайка играет в числа по таким правилам: если число делится на 3 без остатка, то от числа отнимается 1. Если число при делении на 3 даёт в остатке 1, к нему прибавляется 2. Если число при делении на 3 даёт в остатке 2, то от него отнимается 2. В начале игры Незнайка записал число 10000. Какое число у него получится после 2020 ходов?
    (A) 10000 (Б) 6974 (В) 6970 (Г) 3946 (Д) 3940


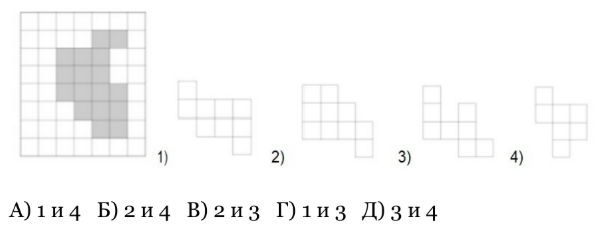
  7. В прямоугольнике на клетчатой бумаге закрасили несколько клеток. Укажите, из каких деталей, нарисованных на рисунках (1)--(4), можно сложить закрашенную область?



Материалы школы Юайти
youit.school ©
Поступление в Школу "Интеллектуал"
Вариант вступительного экзамена в 5 класс (по выбору). 2020 год
Математика базовая. Баллы: все задачи по 4 балла. В задачах 1--4 бинарное оценивание (0/4), в задаче 5 по 1 баллу за каждую верную пару «условие--выражение».


  1. В данном примере расставьте скобки так, чтобы результат вычислений был наибольшим из возможных: $10:11-1\cdot6$. Запишите результат.
    Ответ: \underline{}
    Решение: Возможные варианты: $(:- -)=;$ $(:-)=:;$ $(-)=:;$ $(:)=:$; брать в скобки умножение или деление не даст нового варианта.

  2. Для покраски поверхности площадью 1~дм$^2$ требуется 40 граммов краски. У Пети есть прямоугольный брусок длиной 20~см, шириной 15~см и высотой 10~см. Сколько граммов краски понадобится Пете, чтобы покрасить брусок со всех сторон?
    Ответ: 520 грамм
    Решение: Площадь всей поверхности бруска равна $2(20\cdot15+15\cdot10+20\cdot10)=13$~дм$^2$. Краски нужно $13\cdot40$~г.

  3. Две ватрушки и плюшка вместе стоят 130 рублей. Две ватрушки и три плюшки вместе стоят 210 рублей. Сколько стоят вместе две плюшки и ватрушка?
    Ответ: 125 рублей
    Решение: Разница между 210 и 130 равна как раз стоимости двух плюшек. Значит, плюшка стоит $(210-130):2=40$~руб. Тогда две ватрушки стоят $130-40=90$~руб, одна ватрушка 45~руб, и ватрушка и две плюшки $45+2\cdot40$~руб.

  4. Незнайка и Шпунтик выехали из Цветочного города в Солнечный одновременно. Незнайка ехал на автобусе со скоростью 48~км/ч, а Шпунтик на своём автомобиле со скоростью 72~км/ч. Через 4 часа мотор у Шпунтика заглох, пришлось остановиться и чинить его. Автобус с Незнайкой ехал без остановок. Когда Шпунтик починил мотор, он поехал дальше и ещё через 2 часа догнал автобус. Сколько часов потратил Шпунтик на починку мотора?
    Ответ: 3 часа
    Решение: 1) $(4+2)\cdot72=432$~(км) – проехал Шпунтик до встречи с Незнайкой. 2) $432:48=9$~(ч) – всего ехал Незнайка. 3) $9-6=3$~(ч) – Шпунтик стоял на месте.

  5. Сопоставьте условие каждой задачи с числовым выражением, составленным для её решения.

    Ответ: 1) Б, 2) В, 3) Г, 4) А

    Решение: 1) Вася по 10 страниц в день прочтёт книгу за $250:10$ дней, Петя за $250:5$ дней. Разность показывает, сколько дней больше. 2) Таня потратит на 10 открыток по 5~руб $10\cdot5$~руб, а сдача $250-10\cdot5$. 3) Скорость удаления Матроскина от Печкина равна разности скоростей $250-10$, за 5~ч обгонит на $(250-10)\cdot5$. 4) Площадь прямоугольника – произведение сторон; разность $250\cdot10-250:5$.



Математика по выбору

  1. Галя обнаружила, что сумма точек на противоположных гранях игрального кубика всегда равна семи. Она взяла четыре одинаковых игральных кубика и склеила их, приложив друг к другу одинаковыми гранями. После этого Галя некоторые грани закрасила белой краской. Сколько точек было на грани, отмеченной «звёздочкой»?

    (A) 1 \quad (Б) 2 \quad (В) 3 \quad (Г) 5 \quad (Д) нельзя определить
    Ответ: (Г) 5
    Решение: Кубик, у которого видно три грани, даёт информацию: если смотреть на 2 так, чтобы 6 было сверху, то 1 снизу, 3 справа, 4 слева, 5 на задней грани. Все кубики одинаковы и склеены по одинаковым граням. На ближнем левом кубике напротив 1 будет 6. Значит, на дальнем левом кубике спереди будет тоже 6. Рассуждая так же, получим, что у дальнего левого кубика на правой грани 3. Выбрать между 2 и 5 для верхней грани можно, мысленно повернув правый передний кубик: если смотреть на 6 так, чтобы 3 была справа, то при этом 2 внизу, а 5 вверху.

  2. На рисунках А, Б, В, Г все детали состоят из семи кубиков. Какую из этих деталей не получится составить из кусочков, нарисованных в рамочке?

    Ответ: (Д) все получится
    Решение: Даны кусочки по 3 и 4 кубика. В каждой детали 7 кубиков, значит, слева внизу у детали A «дырка», и везде надо использовать левую верхнюю деталь (7=3+4). Используя по две из них, можно составить любую из нарисованных деталей. Кусочки можно поворачивать. (A) левый нижний + левый верхний; (Б) два верхних; (В) левый верхний + правый нижний; (Г) два верхних.

  3. Попугаи Кеша, Бася и Гоша очень любят орехи. Гоше дали 6 орехов, а Кеше и Басье по 12 таких же орехов. Кеша ест в два раза быстрее, чем Бася. Гоша ест в два раза медленнее, чем Бася. Грызть орехи все попугаи начали одновременно. Кеша съел свою порцию за три минуты, после чего они с Басей вдвоём доели порцию Баси. Через сколько минут после этого Гоша доел свои орехи?
    Ответ: (Г) 2 мин
    Решение: Кеша съел 12 орехов за 3 минуты, значит, скорость Кеши 4 ореха/мин, Бася 2 ореха/мин, Гоша 1 орех/мин. Когда Кеша всё съел, Бася успел съесть 6 орехов. Вместе они едят 6 орехов/мин, то есть порцию Бася они съели за 1 мин после Кешиного финиша. Гоша за 4 минуты съел 4 ореха и осталось 2, значит, до конца он доел за 2 минуты.

  4. Пятиклассницы записали в серые клетки на рисунке какие-то числа. Затем заполнили белые клетки, составив для этих чисел таблицу умножения. После этого несколько чисел стёрли, а несколько — заменили буквами. Какие две из букв заменяют одно и то же число?

    (A) И и К; (Б) Л и Ы; (В) К и О; (Г) Ы и Н; (Д) Ш и Ц
    Ответ: (Б) Л и Ы
    Решение: Пользуясь известными ответами в таблице умножения, восстановим: в верхней строке серые клетки 3,9,2,7; в левом столбце 8,4,3,6. Далее Л=4*3=12, 6*2=12=Ы.

  5. Гномы Торин, Балин и Двалин соревновались в беге на 300 метров. Они начали бег одновременно. Каждый из них бежал с постоянной скоростью. Когда Торин финишировал, Двалин до конца дистанции оставалось 100 метров, а Балин был на 40~м впереди Двалина. Когда Балин финишировал, то на каком расстоянии до конца дистанции был Двалин?
    (A) 20~м \quad (Б) 30~м \quad (В) 40~м \quad (Г) 50~м \quad (Д) 60~м
    Ответ: (Г) 50~м
    Решение: Торин пробежал 300~м за то же время, что Двалин 200~м и Балин 240~м. Скорость Балин/Двалин = 240:200=6:5. Когда Балин пробежал 60~м, Двалин пробежал 50~м, значит, до финиша ему оставалось 50~м.

  6. Незнайка играет в числа по таким правилам: если число делится на 3 без остатка, то от числа отнимается 1. Если число при делении на 3 даёт в остатке 1, к нему прибавляется 2. Если число при делении на 3 даёт в остатке 2, то от него отнимается 2. В начале игры Незнайка записал число 10000. Какое число у него получится после 2020 ходов?
    (A) 10000 \quad (Б) 6974 \quad (В) 6970 \quad (Г) 3946 \quad (Д) 3940
    Ответ: (Б) 6974
    Решение: Начиная с 10000 (остаток 1), следующая последовательность остатков чередуется: 1→... По 2 хода число уменьшается на 3. За 2018 ходов уменьшится на $3\cdot1009=3027$, итого $10000-3027=6973$. Далее последний ход (2020) остаток меняет число по правилу 1→+2, итого $6973+2=6975$.\

  7. В прямоугольнике на клетчатой бумаге закрасили несколько клеток. Укажите, из каких деталей, нарисованных на рисунках (1)--(4), можно сложить закрашенную область?

    Ответ: (Б) 2 и 4
    Решение: В закрашенной фигуре 17 клеток. Фигуры 2 и 4 имеют 10+7=17 клеток.

Материалы школы Юайти