ГБОУ Школа № 1533 «ЛИТ» из 5 в 6 класс 2025

ЛИТ 1533

2025

15.05.2025

1. К задуманному четырёхзначному числу приписали цифру 9 слева. Полученное число уменьшили на 77606, а затем новый результат уменьшили в 15 раз. В итоге получили число, которое на 199 больше числа 854. Найдите задуманное число.
2. Решите уравнение:
   а) $36,91 - (5,7 + 7c + 2,84 + 3c) = 13,9$
   б) $\frac{3}{13} - \frac{12}{48}c - 3 - \frac{1}{13} = \frac{5}{48}c - \frac{40}{13}$
3. Прямоугольник периметра 180 разрезали на восемь одинаковых прямоугольников (смотри рисунок). Сумма длин всех разрезов оказалась равна 110 см. Чему равна площадь каждого из восьми получившихся прямоугольников?
   
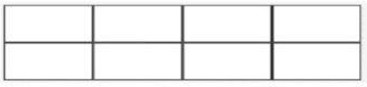
4. Масса одного количества чайных ложек по 9 г такая же, как и масса другого количества чайных ложек по 12 г. Определите, сколько есть тех и других ложек, учитывая, что всего их 105.
5. Маугли попросил восемь обезьян принести ему кокосы. Обезьяны набрали кокосов поровну и понесли Маугли. По дороге они поссорились, и каждая обезьяна бросила в каждую другую по три кокоса. В результате они принесли Маугли на $\frac{7}{8}$ меньше кокосов, чем собрали. Сколько кокосов получил Маугли?
6. По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 70 км/ч и 50 км/ч. Длина пассажирского поезда равна 200 метров. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 45 секундам. Ответ дайте в метрах.
7. В городах А и Б проходит олимпиада по математике. Известно, что в обоих городах олимпиада начиналась в 11 часов утра по местному времени и продолжалась одинаковое время. Оказалось, что в городе А олимпиада закончилась на час раньше, чем начиналась в Б. При этом в Б она заканчивалась на 7 часов позже, чем начиналась в А. Сколько времени длилась олимпиада?

Решения задач

1. К задуманному четырёхзначному числу приписали цифру 9 слева. Полученное число уменьшили на 77606, а затем новый результат уменьшили в 15 раз. В итоге получили число, которое на 199 больше числа 854. Найдите задуманное число.
   Решение: Обозначим задуманное число за \( N \). Приписав слева 9, получаем число \( 90000 + N \). После уменьшения на 77606: \[ 90000 + N - 77606 = 12394 + N \] После деления на 15: \[ \frac{12394 + N}{15} \] По условию: \[ \frac{12394 + N}{15} = 854 + 199 \] \[ \frac{12394 + N}{15} = 1053 \] \[ 12394 + N = 15 \cdot 1053 = 15795 \] \[ N = 15795 - 12394 = 3401 \] Ответ: 3401.
2. Решите уравнение:
   а) \( 36,91 - (5,7 + 7c + 2,84 + 3c) = 13,9 \)
   Решение: Упростим выражение в скобках: \[ 5,7 + 2,84 = 8,54 \quad \text{и} \quad 7c + 3c = 10c \] Подставим в уравнение: \[ 36,91 - (8,54 + 10c) = 13,9 \] \[ 36,91 - 8,54 - 10c = 13,9 \] \[ 28,37 - 10c = 13,9 \] \[ -10c = 13,9 - 28,37 \] \[ -10c = -14,47 \] \[ c = \frac{14,47}{10} = 1,447 \] Ответ: \( 1,447 \). б) \( \frac{3}{13} - \frac{12}{48}c - 3 - \frac{1}{13} = \frac{5}{48}c - \frac{40}{13} \)
   Решение: Приведём подобные слагаемые слева: \[ \left(\frac{3}{13} - \frac{1}{13}\right) - 3 - \left(\frac{12}{48}c + \frac{5}{48}c\right) = -\frac{40}{13} \] \[ \frac{2}{13} - 3 - \frac{17}{48}c = -\frac{40}{13} \] \[ -\frac{37}{13} - \frac{17}{48}c = -\frac{40}{13} \] \[ -\frac{17}{48}c = -\frac{40}{13} + \frac{37}{13} \] \[ -\frac{17}{48}c = -\frac{3}{13} \] \[ c = \frac{3}{13} \cdot \frac{48}{17} = \frac{144}{221} \] Ответ: \( \frac{144}{221} \).
3. Прямоугольник периметра 180 разрезали на восемь одинаковых прямоугольников. Сумма длин всех разрезов оказалась равна 110 см. Чему равна площадь каждого из восьми получившихся прямоугольников?
   Решение: Пусть исходный прямоугольник имеет стороны \( a \) и \( b \). Периметр: \[ 2(a + b) = 180 \quad \Rightarrow \quad a + b = 90 \] Предположим, что прямоугольник разрезали на 4 части по длине и 2 по ширине. Тогда суммарная длина разрезов: \[ 3b + a = 110 \] Решаем систему уравнений: \[ \begin{cases} a + b = 90 \\ 3b + a = 110 \end{cases} \] Вычитаем первое уравнение из второго: \[ 2b = 20 \quad \Rightarrow \quad b = 10 \] \[ a = 90 - 10 = 80 \] Площадь исходного прямоугольника: \[ a \cdot b = 80 \cdot 10 = 800 \] Площадь каждого малого прямоугольника: \[ \frac{800}{8} = 100 \] Ответ: 100 см².
4. Масса одного количества чайных ложек по 9 г такая же, как и масса другого количества чайных ложек по 12 г. Определите, сколько есть тех и других ложек, учитывая, что всего их 105.
   Решение: Пусть \( x \) — количество ложек по 9 г, \( y \) — по 12 г. Условия задачи: \[ \begin{cases} 9x = 12y \\ x + y = 105 \end{cases} \] Из первого уравнения: \[ 3x = 4y \quad \Rightarrow \quad y = \frac{3}{4}x \] Подставляем во второе уравнение: \[ x + \frac{3}{4}x = 105 \] \[ \frac{7}{4}x = 105 \quad \Rightarrow \quad x = 60 \] \[ y = 105 - 60 = 45 \] Ответ: 60 и 45.
5. Маугли попросил восемь обезьян принести ему кокосы. Обезьяны набрали кокосов поровну и понесли Маугли. По дороге они поссорились, и каждая обезьяна бросила в каждую другую по три кокоса. В результате они принесли Маугли на \(\frac{7}{8}\) меньше кокосов, чем собрали. Сколько кокосов получил Маугли?
   Решение: Пусть каждая обезьяна собрала \( k \) кокосов. Всего собрали: \[ 8k \] Каждая обезьяна бросила в 7 других по 3 кокоса, потратив: \[ 3 \cdot 7 = 21 \text{ кокос} \] Всего потрачено: \[ 8 \cdot 21 = 168 \text{ кокосов} \] Оставшиеся кокосы: \[ 8k - 168 = \frac{1}{8} \cdot 8k \] \[ 8k - 168 = k \quad \Rightarrow \quad 7k = 168 \quad \Rightarrow \quad k = 24 \] Маугли получил: \[ \frac{1}{8} \cdot 8k = k = 24 \] Ответ: 24.
6. По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 70 км/ч и 50 км/ч. Длина пассажирского поезда равна 200 метров. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 45 секундам. Ответ дайте в метрах.
   Решение: Относительная скорость: \[ 70 + 50 = 120 \text{ км/ч} = \frac{120000}{3600} = 33\frac{1}{3} \text{ м/с} \] Путь за 45 секунд: \[ 33\frac{1}{3} \cdot 45 = 1500 \text{ м} \] Сумма длин поездов: \[ 1500 - 200 = 1300 \text{ м} \] Ответ: 1300.
7. В городах А и Б проходит олимпиада по математике. Известно, что в обоих городах олимпиада начиналась в 11 часов утра по местному времени и продолжалась одинаковое время. Оказалось, что в городе А олимпиада закончилась на час раньше, чем начиналась в Б. При этом в Б она заканчивалась на 7 часов позже, чем начиналась в А. Сколько времени длилась олимпиада?
   Решение: Пусть олимпиада длилась \( x \) часов, а разница во времени между городами \( t \) часов. Из условий задачи: \[ \begin{cases} 11 + x = 11 - t - 1 \\ 11 + x - t = 11 + 7 \end{cases} \] Решаем первое уравнение: \[ x = -t - 1 \] Второе уравнение: \[ x - t = 7 \] Подставляем \( x = -t - 1 \): \[ -t - 1 - t = 7 \quad \Rightarrow \quad -2t = 8 \quad \Rightarrow \quad t = -4 \] Тогда: \[ x = -(-4) - 1 = 4 - 1 = 3 \] Ответ: 3 часа.