ГБОУ РМ Республиканский лицей из 6 в 7 класс 2021

1. Вычислите без калькулятора: \[ \frac{\tfrac{2}{5} : \bigl(1 - \tfrac{4}{7}\bigr) - \bigl(\tfrac{4}{3} + \tfrac{2}{5}\bigr) : \bigl(\tfrac{2}{3} + \tfrac{5}{6}\bigr) \cdot \tfrac{26}{27}} { } = \]
   
   
2. На заключительном этапе Всероссийской олимпиады школьников по физике общее число дипломантов (победителей и призёров) не должно превышать 45% от числа участников. Какое минимальное количество участников может оказаться без дипломов, если в олимпиады принимает участие 302 школьника?
   
   
3. Вычислите (без калькулятора) значение выражения при \(a=2020\) и \(b=2021\): \[ \frac{\tfrac{b}{a}\;\cdot\;\bigl(1 + \tfrac{a}{b}\bigr)} {1 + \tfrac{b}{a}} \;\cdot\; \frac{b^2 - a^2}{a + b} = \]
   
   
4. Решите систему уравнений: \[ \begin{cases} x + 1{,}5y = 8,\\ 7x - 3y = 2. \end{cases} \]
   
   
5. Муравей хочет быстрее добраться по кубу из точки \(A\) в точку \(B\) (см. рисунок).
   
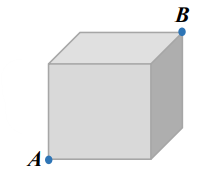
   Какой маршрут ему следует выбрать? Обоснуйте свой ответ.
   
   
6. Два спортсмена стартуют одновременно из одной точки и бегут по кольцевой дорожке стадиона длиной \(S = 400\)м. Через какое время \(t\) один бегун обгонит другого на целый круг, если его скорость больше скорости отстающего на \(\Delta v = 1{,}8\)км/ч? Сколько кругов пробежит отстающий бегун, если его скорость \(v = 2\)м/с?
   
   
7. Первую треть всего пути велосипедист проехал за половину всего времени движения со скоростью \(v = 10\)км/ч. Найдите среднюю скорость велосипедиста на всём пути.

Решения задач

1. Вычислите без калькулятора: \[ \frac{\tfrac{2}{5} : \bigl(1 - \tfrac{4}{7}\bigr) - \bigl(\tfrac{4}{3} + \tfrac{2}{5}\bigr) : \bigl(\tfrac{2}{3} + \tfrac{5}{6}\bigr) \cdot \tfrac{26}{27}} { } \] Решение:
   Найдем значение выражения по частям:
   1) $1 - \frac{4}{7} = \frac{3}{7}$
   $\tfrac{2}{5} : \tfrac{3}{7} = \tfrac{14}{15}$
   2) $\tfrac{4}{3} + \tfrac{2}{5} = \tfrac{26}{15}$
   $\tfrac{2}{3} + \tfrac{5}{6} = \tfrac{9}{6} = \tfrac{3}{2}$
   $\tfrac{26}{15} : \tfrac{3}{2} = \tfrac{52}{45}$
   $\tfrac{52}{45} \cdot \tfrac{26}{27} = \tfrac{1352}{1215}$
   3) Вычислим числитель:
   $\tfrac{14}{15} - \tfrac{1352}{1215} = \tfrac{1134}{1215} - \tfrac{1352}{1215} = -\tfrac{218}{1215}$
   Ответ: $-\dfrac{218}{1215}$.
   
   
2. На заключительном этапе Всероссийской олимпиады школьников по физике общее число дипломантов не должно превышать 45% от числа участников. Какое минимальное количество участников может оказаться без дипломов, если в олимпиаде участвует 302 школьника?
   Решение:
   Максимальное число дипломантов: $302 \cdot 0,45 = 135,9 \approx 135$.
   Минимальное число участников без дипломов: $302 - 135 = 167$.
   Ответ: 167.
   
   
3. Вычислите значение выражения при \(a=2020\) и \(b=2021\): \[ \frac{\tfrac{b}{a}\;\cdot\;\bigl(1 + \tfrac{a}{b}\bigr)} {1 + \tfrac{b}{a}} \;\cdot\; \frac{b^2 - a^2}{a + b} \] Решение:
   Упростим выражение:
   1) $\tfrac{b}{a} \cdot (1 + \tfrac{a}{b}) = \tfrac{b + a}{a}$
   2) $1 + \tfrac{b}{a} = \tfrac{a + b}{a}$
   3) Вся дробь сводится к $1$.
   4) $\tfrac{b^2 - a^2}{a + b} = b - a$
   При подстановке: $2021 - 2020 = 1$.
   Ответ: 1.
   
   
4. Решите систему уравнений: \[ \begin{cases} x + 1{,}5y = 8,\\ 7x - 3y = 2. \end{cases} \] Решение:
   Выразим \( x \) из первого уравнения:
   \( x = 8 - 1,5y \)
   Подставим во второе уравнение:
   \( 7(8 - 1,5y) - 3y = 2 \)
   \( 56 - 10,5y - 3y = 2 \)
   \( -13,5y = -54 \)
   \( y = 4 \)
   \( x = 8 - 1,5 \cdot 4 = 2 \)
   Ответ: \( x = 2 \), \( y = 4 \).
   
   
5. Муравей хочет добраться по кубу из точки \(A\) в точку \(B\). Какой маршрут выбрать?
   Решение:
   Кратчайший путь по поверхности куба – развертка куба на плоскости. Оптимальный маршрут проходит через две смежные грани, образуя прямоугольный треугольник. Длина пути равна \( \sqrt{(a + a)^2 + a^2} = a\sqrt{5} \), где \( a \) – длина ребра куба.
   Ответ: маршрут по двум смежным граням, длина \( a\sqrt{5} \).
   
   
6. Два спортсмена бегут по кольцевой дорожке длиной 400 м. Через какое время один обгонит другого на целый круг?
   Решение:
   Разница скоростей: \( \Delta v = 1,8 \, \text{км/ч} = 0,5 \, \text{м/с} \).
   Время обгона: \( t = \tfrac{S}{\Delta v} = \tfrac{400}{0,5} = 800 \, \text{с} = 13 \, \text{мин} \, 20 \, \text{с} \).
   Отстающий бегун пробежит: \( v = 2 \, \text{м/с} \cdot 800 \, \text{с} = 1600 \, \text{м} = 4 \, \text{круга} \).
   Ответ: 800 с (13 мин 20 с), 4 круга.
   
   
7. Найдите среднюю скорость велосипедиста.
   Решение:
   Пусть общее время движения \( T \). Первые \( \tfrac{S}{3} \) пройдены за \( \tfrac{T}{2} \) со скоростью 10 км/ч:
   \( \tfrac{S}{3} = 10 \cdot \tfrac{T}{2} \Rightarrow \tfrac{S}{T} = 15 \, \text{км/ч} \).
   Ответ: 15 км/ч.