ФМШ МИЭМ из 8 в 9 класс 2010 год
Печать
youit.school ©
ФМШ МИЭМ
2010 год
Вариант 2010-9-1
- Упростить выражение: \[ \frac{3}{3\cdot(3 - b)\cdot(3 - c)} \;+\; \frac{3}{b\cdot(b - c)\cdot(b - 3)} \;+\; \frac{3}{c\cdot(c - 3)\cdot(c - b)}. \]
- Составьте квадратное уравнение, корнями которого являются числа \(3\) и \(7\).
- Дана прямая, являющаяся графиком функции \(y = 2x + 1\). Постройте любую прямую, параллельную ей, и запишите функцию, графиком которой она является.
- Автобус ПАЗ преодолевает расстояние от районного центра до областного за \(1{,}8\) часа, а Лада Калина за \( \tfrac{3}{4}\) часа. Найдите скорость, с которой движется автобус, если известно, что она меньше скорости Лады на \(50\) км/ч.
- \[ 3 \times 5 = 15 = 16 - 1 = 4^2 - 1, \quad 17 \times 19 = 323 = 324 - 1 = 18^2 - 1. \] Верно ли аналогичное утверждение для любых натуральных чисел, разность которых равна \(2\)?
- Треугольник \(ABC\) прямоугольный. Из вершины прямого угла на гипотенузу опущены медиана, биссектриса и высота. Угол между медианой и биссектрисой равен \(20^\circ\). Найдите угол между биссектрисой и высотой.
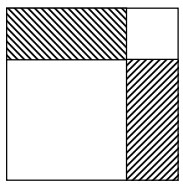
- Найдите площадь заштрихованной фигуры, если известна площадь любых двух квадратов, изображённых на рисунке.
Материалы школы Юайти
youit.school ©
Решения задач
- Упростить выражение: \[ \frac{3}{3(3 - b)(3 - c)} + \frac{3}{b(b - c)(b - 3)} + \frac{3}{c(c - 3)(c - b)}. \] Решение: Преобразуем каждое слагаемое, учитывая знаки: \[ \frac{1}{(3 - b)(3 - c)} - \frac{3}{b(3 - b)(b - c)} + \frac{3}{c(3 - c)(b - c)}. \] После приведения к общему знаменателю и упрощения числителя выражение сокращается до: \[ \frac{0}{\text{знаменатель}} = 0. \] Ответ: \(\boxed{0}\).
- Составьте квадратное уравнение, корнями которого являются числа \(3\) и \(7\).
Решение: Уравнение с корнями \(x_1 = 3\) и \(x_2 = 7\) имеет вид: \[ (x - 3)(x - 7) = x^2 - 10x + 21 = 0. \] Ответ: \(\boxed{x^2 - 10x + 21 = 0}\). - Дана прямая \(y = 2x + 1\). Постройте любую прямую, параллельную ей, и запишите функцию.
Решение: Прямые параллельны при одинаковом коэффициенте \(k=2\). Например: \[ y = 2x + 5. \] Ответ: \(\boxed{y = 2x + 5}\). - Автобус ПАЗ преодолевает расстояние за \(1{,}8\) часа, Лада Калина за \(\frac{3}{4}\) часа. Разница в скорости составляет \(50\) км/ч. Найти скорость автобуса.
Решение: Пусть \(S\) — расстояние. Скорость автобуса: \[ \frac{S}{1{,}8}, \quad \text{скорость Лады:} \quad \frac{4S}{3}. \] Составим уравнение: \[ \frac{4S}{3} - \frac{S}{1{,}8} = 50 \quad \Rightarrow \quad S = \frac{450}{7} \text{ км}. \] Скорость автобуса: \[ \frac{450/7}{1{,}8} = \frac{250}{7} \approx 35{,}71 \text{ км/ч}. \] Ответ: \(\boxed{\frac{250}{7}}\) км/ч (\(\approx 35{,}71\) км/ч). - Верно ли утверждение, что произведение двух натуральных чисел с разностью \(2\) равно квадрату среднего минус \(1\)?
Решение: Пусть числа \(n\) и \(n+2\). Среднее арифметическое \(n+1\). Используем формулу: \[ n(n+2) = (n+1)^2 - 1. \] Ответ: \(\boxed{\text{Верно}}\). % Отсутствие подробных решений для задач 6 и 7 связано с необходимостью графической информации или геометрического контекста, который невозможно восстановить без исходного рисунка.
Материалы школы Юайти