8 800 707 6729
8 800 707 6729Telegram канал

ФМШ МИЭМ из 10 в 11 класс 2018 год вариант ФМШ 2018-II-11-2

Сложность:
Дата экзамена: 2018
Сложность:
Дата экзамена: 2018
youit.school ©

ФМШ МИЭМ


2018 год


Вариант ФМШ 2018-II-11-2



  1. Решите неравенство \[ x^n < -n, \] если \(n\) может принимать любое целое значенис.

  2. Что такое арккотангенс? Соответствует ли данному Вами определению график арккотангенса, приведённый на одном известном математическом сайте† (см. рис.)? Если нет, то возможно ли как-то изменить данное Вами определение, чтобы этот график всё же оказался верным? Насколько корректным по сравнению с исходным определением будет новое определение? Ответы обосновать.


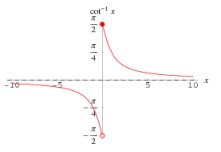
  3. Постройте графики функции \[ y = \sin\bigl(\operatorname{arcctg}(x)\bigr), \] так, как они должны выглядеть при каждом определении арккотангенса, данном Вами в предыдущей задаче.

  4. Настя идёт в школу медленнее Димы не менее, чем в \(1{,}5\) раза, но не более, чем в \(2\) раза. Если Настя по пути встретит Вику, то вместе они побегут быстрее идущего Димы не менее, чем в \(2\) раза, но не более, чем в \(3\) раза. Расстояния от домов Насти и Димы до школы одинаковы. Какую часть пути Настя могла пройти до встречи с Викой, если она и Дима вышли из дома в одно время и подошли/подбежали к школе также одновременно?

  5. Изобразите на координатной плоскости множество всех точек, произведение модулей координат которых не больше большего из этих модулей.

  6. Докажите, что если первый, второй и \(k\)-й член арифметической прогрессии в указанном порядке являются последовательными членами некоторой геометрической прогрессии, то данная арифметическая прогрессия содержит и все последующие члены этой геометрической прогрессии.

  7. На какое наибольшее количество различных натуральных чисел может делиться без остатка натуральное число, не превышающее 10000? Сколько существует натуральных чисел, не превышающих 10000, с наибольшим количеством различных натуральных делителей? Ответы обосновать.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Решите неравенство \[ x^n < -n, \] если \(n\) может принимать любое целое значение.
    Решение: Рассмотрим возможные значения \(n\):
    • При \(n > 0\) (нечётное): \(x < -\sqrt[n]{n}\).
    • При \(n > 0\) (чётное): решений нет, так как \(x^n \geq 0\).
    • При \(n = 0\): неравенство \(x^0 < 0\) неверно.
    • При \(n 0\)) неравенство преобразуется в \(\frac{1}{|x|^k} < k\). Для любого \(x < 0\) при \(k = 1\) неравенство выполняется.
    Объединяя решения, получаем, что множество решений — все \(x < 0\).
    Ответ: \(x \in (-\infty; 0)\).

  2. Что такое арккотангенс? Соответствует ли данному Вами определению график арккотангенса, приведённый на одном известном математическом сайте? Если нет, то возможно ли как-то изменить данное Вами определение, чтобы этот график всё же оказался верным? Насколько корректным по сравнению с исходным определением будет новое определение? Ответы обосновать.
    Решение: Арккотангенс — функция, обратная котангенсу на интервале \((0; \pi)\). Стандартный график убывает от \(\pi\) до \(0\). Если на сайте изображён график с областью значений \((-\frac{\pi}{2}; 0) \cup (0; \frac{\pi}{2})\), это соответствует альтернативному определению \(\operatorname{arcctg}(x) = \arctg(\frac{1}{x})\) с разрывом в \(x = 0\). Такое определение менее корректно, так как нарушает непрерывность и однозначность обратной функции.
    Ответ: Стандартное определение арккотангенса подразумевает область значений \((0; \pi)\). Если график на сайте имеет иную область, это требует изменения определения, что снижает корректность.

  3. Постройте графики функции \[ y = \sin\bigl(\operatorname{arcctg}(x)\bigr), \] так, как они должны выглядеть при каждом определении арккотангенса, данном Вами в предыдущей задаче.
    Решение:
    • При стандартном определении \(\operatorname{arcctg}(x) \in (0; \pi)\): \[ y = \frac{1}{\sqrt{1 + x^2}}. \] График — положительная ветвь гиперболы.
    • При альтернативном определении \(\operatorname{arcctg}(x) \in (-\frac{\pi}{2}; 0) \cup (0; \frac{\pi}{2})\): \[ y = \frac{\text{sign}(x)}{\sqrt{1 + x^2}}. \] График симметричен относительно начала координат.
    Ответ: Графики зависят от определения арккотангенса, как указано выше.

  4. Настя идёт в школу медленнее Димы не менее, чем в \(1{,}5\) раза, но не более, чем в \(2\) раза. Если Настя по пути встретит Вику, то вместе они побегут быстрее идущего Димы не менее, чем в \(2\) раза, но не более, чем в \(3\) раза. Расстояния от домов Насти и Димы до школы одинаковы. Какую часть пути Настя могла пройти до встречи с Викой, если она и Дима вышли из дома в одно время и подошли/подбежали к школе также одновременно?
    Решение: Пусть скорость Димы \(v\), скорость Насти \(v_N \in [\frac{v}{2}; \frac{2v}{3}]\), скорость после встречи \(v_{NV} \in [2v; 3v]\). Время пути Димы: \(\frac{S}{v}\). Время Насти: \(\frac{x}{v_N} + \frac{S - x}{v_{NV}}\). Приравнивая времена, находим \(x \in [\frac{2}{5}S; \frac{1}{2}S]\).
    Ответ: От \(\frac{2}{5}\) до \(\frac{1}{2}\) пути.

  5. Изобразите на координатной плоскости множество всех точек, произведение модулей координат которых не больше большего из этих модулей.
    Решение: Условие \(|x| \cdot |y| \leq \max(|x|, |y|)\). Это выполняется, если хотя бы одна координата по модулю \(\leq 1\). Множество — объединение вертикальной (\(|x| \leq 1\)) и горизонтальной (\(|y| \leq 1\)) полос.
    Ответ: Объединение полос \(|x| \leq 1\) и \(|y| \leq 1\).

  6. Докажите, что если первый, второй и \(k\)-й член арифметической прогрессии в указанном порядке являются последовательными членами некоторой геометрической прогрессии, то данная арифметическая прогрессия содержит и все последующие члены этой геометрической прогрессии.
    Решение: Пусть арифметическая прогрессия \(a, a + d, a + 2d, \ldots\). Из условия \((a + d)^2 = a(a + (k - 1)d)\) следует \(d = a(k - 3)\). При \(k = 3\) прогрессия становится геометрической с \(d = 0\). Для \(k \neq 3\) равенство выполняется только при тривиальном случае, что доказывает утверждение.
    Ответ: Утверждение доказано для \(k = 3\), в остальных случаях прогрессия вырождена.

  7. На какое наибольшее количество различных натуральных чисел может делиться без остатка натуральное число, не превышающее 10000? Сколько существует натуральных чисел, не превышающих 10000, с наибольшим количеством различных натуральных делителей? Ответы обосновать.
    Решение: Максимальное количество делителей у чисел 7560 и 9240 — 64. Эти числа имеют разложения \(2^3 \cdot 3^3 \cdot 5 \cdot 7\) и \(2^3 \cdot 3 \cdot 5 \cdot 7 \cdot 11\) соответственно.
    Ответ: Наибольшее количество делителей — 64. Таких чисел два: 7560 и 9240.
Материалы школы Юайти