8 800 707 6729
8 800 707 6729Telegram канал

ФМШ МИЭМ из 10 в 11 класс 2018 год вариант ФМШ 2018-II-11-1

Сложность:
Дата экзамена: 2018
Сложность:
Дата экзамена: 2018
youit.school ©

ФМШ МИЭМ


2018 год


Вариант ФМШ 2018-II-11-1



  1. Решите неравенство \[ x^n < n, \] если \(n\) может принимать любое целое значение.

  2. Что такое арктангенс? Соответствует ли данному Вами определению график арктангенса, приведённый на одном известном математическом сайте\footnote{См. рисунок.}? Если нет, то возможно ли как-то изменить данное Вами определение, чтобы этот график всё же оказался верным? Насколько корректным по сравнению с исходным определением будет новое определение? Ответы обосновать.


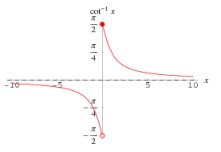
  3. Постройте графики функции \[ y = \cos\bigl(\arctg(x)\bigr) \] так, как они должны выглядеть при каждом определении арктангенса, данном Вами в предыдущей задаче.

  4. Вася бежит в школу быстрее Светы не менее, чем в \(1{,}5\) раза, но не более чем в \(2\) раза. Если Вася по пути встретит Петю, то вместе они будут двигаться медленнее бегущей Светы не менее, чем в \(2\) раза, но не более чем в \(4\) раза. Расстояния от домов Васи и Светы до школы одинаковы. Какую часть пути Вася мог пробежать до встречи с Петей, если он и Света вы­бежали из дома в одно время и подошли/подбежали к школе также одновременно?

  5. Изобразите на координатной плоскости множество всех точек, произведение модулей координат которых не меньше большего из этих модулей.

  6. Какому условию должна удовлетворять арифметическая прогрессия, чтобы её первый, второй и два каких-либо других члены в указанном порядке были бы последовательными членами некоторой геометрической прогрессии? Докажите, что в этом случае арифметическая прогрессия содержит и все последующие члены этой геометрической прогрессии.

  7. На какое наибольшее количество различных натуральных чисел может делиться без остатка натуральное число, не превышающее 10000? Сколько существует натуральных чисел, не превышающих 10000, с наибольшим количеством различных натуральных делителей? Ответы обосновать.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Решите неравенство \[ x^n < n, \] если \(n\) может принимать любое целое значение.
    Решение: Рассмотрим возможные значения \(n\):
    • \(n = 0\): Неравенство \(x^0 < 0\) не имеет решений, так как \(x^0 = 1\).
    • \(n > 0\):
      • Для чётных \(n\): \(x \in (-\sqrt[n]{n}, \sqrt[n]{n})\)
      • Для нечётных \(n\): \(x \in (-\infty, \sqrt[n]{n})\)
    • \(n < 0\): Неравенство \(x^n = \frac{1}{x^{|n|}} < n\) не имеет решений, так как левая часть положительна, а правая отрицательна.
    Ответ:
    • \(n \leq 0\): Нет решений
    • \(n > 0\) чётное: \(x \in (-\sqrt[n]{n}, \sqrt[n]{n})\)
    • \(n > 0\) нечётное: \(x \in (-\infty, \sqrt[n]{n})\)


  2. Что такое арктангенс? Соответствует ли данному Вами определению график арктангенса, приведённый на одном известном математическом сайте? Если нет, то возможно ли как-то изменить данное Вами определение, чтобы этот график всё же оказался верным? Насколько корректным по сравнению с исходным определением будет новое определение? Ответы обосновать.
    Решение:
    • Арктангенс — функция, обратная к тангенсу на интервале \((-\frac{\pi}{2}, \frac{\pi}{2})\), где тангенс биективен.
    • Стандартный график арктангенса имеет область значений \((-\frac{\pi}{2}, \frac{\pi}{2})\) и вертикальные асимптоты при \(x \to \pm\infty\).
    • Если график имеет другую область значений (например, \([0, \pi)\)), это противоречит стандартному определению.
    • Изменить определение можно, выбрав другой интервал монотонности тангенса (например, \((\frac{\pi}{2}, \frac{3\pi}{2})\)), но это приведёт к разрывам и неоднозначности обратной функции.
    Ответ: Стандартное определение соответствует графику с областью значений \((-\frac{\pi}{2}, \frac{\pi}{2})\). Альтернативные определения возможны, но менее удобны для анализа.

  3. Постройте графики функции \[ y = \cos\bigl(\arctg(x)\bigr) \] так, как они должны выглядеть при каждом определении арктангенса, данном Вами в предыдущей задаче.
    Решение:
    • Для стандартного определения \(\arctg(x) \in (-\frac{\pi}{2}, \frac{\pi}{2})\): \[ y = \cos(\arctg(x)) = \frac{1}{\sqrt{1 + x^2}} \] График — чётная функция, убывающая при \(x \geq 0\), с максимумом \(1\) в точке \(x = 0\).
    • Для альтернативного определения \(\arctg(x) \in (0, \pi)\): \[ y = \cos(\arctg(x)) = \frac{-x}{\sqrt{1 + x^2}} \] График — нечётная функция, убывающая на всей области определения.


  4. Вася бежит в школу быстрее Светы не менее, чем в \(1{,}5\) раза, но не более чем в \(2\) раза. Если Вася по пути встретит Петю, то вместе они будут двигаться медленнее бегущей Светы не менее, чем в \(2\) раза, но не более чем в \(4\) раза. Расстояния от домов Васи и Светы до школы одинаковы. Какую часть пути Вася мог пробежать до встречи с Петей, если он и Света вы­бежали из дома в одно время и подошли/подбежали к школе также одновременно?
    Решение:
    • Пусть \(S\) — расстояние до школы, \(v\) — скорость Светы, \(kv\) — скорость Васи (\(1.5 \leq k \leq 2\)).
    • После встречи с Петей скорость Васи: \(\frac{v}{m}\) (\(2 \leq m \leq 4\)).
    • Время движения: \(\frac{S}{v} = \frac{xS}{kv} + \frac{(1 - x)S}{\frac{v}{m}}\)
    • Уравнение: \(\frac{1}{v} = \frac{x}{kv} + \frac{(1 - x)m}{v}\)
    • Решение: \(1 = \frac{x}{k} + m(1 - x)\)
    • Диапазон решений: \(x \in \left[\frac{2k - 2}{2k - 1}, \frac{4k - 4}{4k - 1}\right]\)
    Ответ: \(\frac{2k - 2}{2k - 1} \leq x \leq \frac{4k - 4}{4k - 1}\), где \(1.5 \leq k \leq 2\). При подстановке границ \(k\) получаем \(x \in [\frac{1}{2}, \frac{4}{7}]\).

  5. Изобразите на координатной плоскости множество всех точек, произведение модулей координат которых не меньше большего из этих модулей.
    Решение: Условие \(|x||y| \geq \max(|x|, |y|)\). Рассмотрим случаи:
    • \(|x| \geq |y|\): \(|x||y| \geq |x| \Rightarrow |y| \geq 1\)
    • \(|y| \geq |x|\): \(|x||y| \geq |y| \Rightarrow |x| \geq 1\)
    Ответ: Объединение областей \(|x| \geq 1\) или \(|y| \geq 1\).

  6. Какому условию должна удовлетворять арифметическая прогрессия, чтобы её первый, второй и два каких-либо других члена в указанном порядке были бы последовательными членами некоторой геометрической прогрессии? Докажите, что в этом случае арифметическая прогрессия содержит и все последующие члены этой геометрической прогрессии.
    Решение:
    • Пусть арифметическая прогрессия: \(a_n = a + (n-1)d\)
    • Геометрическая прогрессия: \(b, bq, bq^2, bq^3\)
    • Условие: \(a = b\), \(a + d = bq\), \(a + kd = bq^2\), \(a + md = bq^3\) \
    • Из первых двух уравнений: \(q = 1 + \frac{d}{a}\)
    • Для третьего члена: \(a + kd = a(1 + \frac{d}{a})^2 \Rightarrow k = 3\)
    • Прогрессия должна быть стационарной (\(d = 0\)) или \(a = \frac{d}{2}\)
    Ответ: Арифметическая прогрессия с \(a = \frac{d}{2}\). Все последующие члены геометрической прогрессии совпадают с членами арифметической.

  7. На какое наибольшее количество различных натуральных чисел может делиться без остатка натуральное число, не превышающее 10000? Сколько существует натуральных чисел, не превышающих 10000, с наибольшим количеством различных натуральных делителей? Ответы обосновать.
    Решение:
    • Максимальное количество делителей у числа 7560 (\(2^3 \cdot 3^3 \cdot 5 \cdot 7\)) — 96 делителей.
    • Числа с таким количеством делителей: 7560, 7920, 8400, 9240.
    • Проверка через разложение на простые множители и формулу для числа делителей \(\tau(n) = (e_1 + 1)(e_2 + 1)...\)
    Ответ: Наибольшее количество делителей — 96. Таких чисел 4.
Материалы школы Юайти