ФМШ МИЭМ из 10 в 11 класс 2017 год
Печать
youit.school ©
ФМШ МИЭМ
2017 год
Вариант ФМШ 2017-11-2
- Решите уравнение:
\[
\arccos x + \operatorname{arcctg}x = \frac{\pi}{2}.
\]
- Что называется вертикальной асимптотой? Может ли для одной функции существовать несколько различных вертикальных асимптот? Может ли график функции пересекать свою вертикальную асимптоту? Ответы обоснуйте.
- Постройте график функции:
\[
y = \frac{\bigl\lvert\lvert x\rvert^3 - x^4\bigr\rvert}{2\,\lvert x\rvert\,\sqrt{x - x^2}},
\qquad
y = \frac{\lvert x\rvert - 2\sqrt{x}}{\lvert 1 - \lvert x\rvert\rvert}.
\]
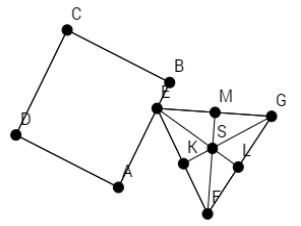
- На плоскости нарисованы квадрат и правильный треугольник с одинаковыми длинами сторон, имеющие одну общую точку $E$. Из этой точки начинают движение с постоянными скоростями два точечных объекта: первый движется по сторонам квадрата
\[
E \to B \to C \to D \to A \to E \to \dots,
\]
а второй — по сторонам и высотам треугольника
\[
E \to F \to M \to E \to L \to G \to K \to E \to \dots.
\]
Каким может быть отношение скоростей данных объектов, чтобы через некоторое время они снова одновременно оказались в точке $E$? Смогут ли они когда-либо снова одновременно оказаться в точке $E$, если скорость одного из объектов будет в 3 раза больше скорости другого?
- Решите неравенство:
\[
3^{6x} > 9^{3x}.
\]
- Найдите все функции $f(x)$, которые для любых действительных значений $x$ удовлетворяют условию:
\[
f(x) - x\,f(1 - x) = 1.
\]
- При каких значениях параметров $a$ и $b$ система \[ \begin{cases} \sin(x + y) = 0, \\ (x - a)^2 + (y - b)^2 < \dfrac{\pi^2}{8}, \\ a^2 + b^2 = \dfrac{9\pi^2}{4} \end{cases} \] не имеет решений?
Материалы школы Юайти
youit.school ©
Решения задач
- Решите уравнение:
\[
\arccos x + \operatorname{arcctg}x = \frac{\pi}{2}.
\]
Решение:
Используем свойство обратных функций для связанных аргументов. Пусть \( \arccos x = \alpha \). Тогда \( x = \cos \alpha \).
Для \( \operatorname{arcctg} x = \operatorname{arcctg}(\cos \alpha) \) воспользуемся тождеством \( \operatorname{arcctg}(\cos \alpha) = \alpha \) при условии \( \alpha \in \left(0, \frac{\pi}{2}\right] \).
Подставляя в исходное уравнение: \[ \alpha + \alpha = \frac{\pi}{2} \Rightarrow 2\alpha = \frac{\pi}{2} \Rightarrow \alpha = \frac{\pi}{4}. \] Тогда \( x = \cos \frac{\pi}{4} = \frac{\sqrt{2}}{2} \).
Проверка показывает, что это решение удовлетворяет уравнению. Если \( x = \frac{\sqrt{2}}{2} \), то \( \arccos x = \frac{\pi}{4} \), \( \operatorname{arcctg} x = \frac{\pi}{4} \), сумма \( \frac{\pi}{4} + \frac{\pi}{4} = \frac{\pi}{2} \).
Ответ: \( \boxed{\dfrac{\sqrt{2}}{2}} \).
- Что называется вертикальной асимптотой? Может ли для одной функции существовать несколько различных вертикальных асимптот? Может ли график функции пересекать свою вертикальную асимптоту?
Решение:- Вертикальной асимптотой графика функции называется прямая \( x = a \), если при приближении \( x \) к \( a \) (слева или справа) значения функции стремятся к \( +\infty \) или \( -\infty \).
- Да, функция может иметь несколько вертикальных асимптот. Например, \( y = \frac{1}{(x - 1)(x + 1)} \) имеет вертикальные асимптоты \( x = 1 \) и \( x = -1 \).
- Нет, график функции не может пересекать вертикальную асимптоту \( x = a \), так как функция не определена в точке \( a \), а вертикальная асимптота — это граница области определения.
- Постройте график функции:
\[
y = \frac{\bigl\lvert\lvert x\rvert^3 - x^4\bigr\rvert}{2\,\lvert x\rvert\,\sqrt{x - x^2}}.
\]
Решение:
Упростим выражение. Для \( x \in (0,1) \):
\[
y = \frac{|x^3 - x^4|}{2x\sqrt{x - x^2}} = \frac{x^3(1 - x)}{2x\sqrt{x(1 - x)}} = \frac{x^2(1 - x)}{2\sqrt{x(1 - x)}} = \frac{x^{3/2}\sqrt{1 - x}}{2}.
\]
График функции на интервале \( (0,1) \) имеет вид возрастающей до точки максимума (при \( x \approx 0.6 \)) и спадающей до нуля при \( x \to 1 \). В точках \( x = 0 \) и \( x = 1 \) функция равна нулю.
Для функции: \[ y = \frac{\lvert x\rvert - 2\sqrt{x}}{\lvert 1 - \lvert x\rvert\rvert}. \] Рассмотрим два случая:- При \( x \in [0,1) \): \( |1 - x| = 1 - x \), тогда \[ y = \frac{x - 2\sqrt{x}}{1 - x}. \]
- При \( x > 1 \): \( |1 - x| = x - 1 \), тогда \[ y = \frac{x - 2\sqrt{x}}{x - 1}. \]
- Найдите отношение скоростей объектов, движущихся по квадрату и треугольнику, чтобы они вернулись в точку \( E \) одновременно. Возможно ли это при отношении скоростей \( 3:1 \)?
Решение:
Длина пути первого объекта (по квадрату): \( 4a \). Период: \( T_1 = \frac{4a}{v_1} \). Для второго объекта: - Правильный треугольник со стороной \( a \). - Путь включает движение по сторонам и высотам. Полный цикл: длина пути \( 6a \). Период: \( T_2 = \frac{6a}{v_2} \).
Условие возврата: \( kT_1 = mT_2 \), где \( k, m \in \mathbb{N} \). Отношение скоростей: \[ \frac{v_1}{v_2} = \frac{4}{6} \cdot \frac{m}{k} = \frac{2}{3} \cdot \frac{m}{k}. \]
Любое рациональное отношение вида \( \frac{2m}{3k} \). При \( \frac{v_1}{v_2} = 3 \) или \( \frac{1}{3} \) невозможно подобрать целые \( m, k \), так как \( \frac{2m}{3k} = 3 \) приводит к \( m = \frac{9k}{2} \), что не является целым для целых \( k \).
Ответ: Отношение скоростей должно быть рациональным кратным \( \frac{2}{3} \). При отношении \( 3:1 \) невозможно.
- Решите неравенство:
\[
3^{6x} > 9^{3x}.
\]
Решение: \( 9^{3x} = (3^2)^{3x} = 3^{6x} \). Получаем \( 3^{6x} > 3^{6x} \), что невозможно. Решений нет.
Ответ: \( \boxed{\varnothing} \).
- Найдите все функции \( f(x) \), удовлетворяющие условию:
\[
f(x) - x f(1 - x) = 1.
\]
Решение: Подставим \( x \rightarrow 1 - x \):
\[
f(1 - x) - (1 - x)f(x) = 1.
\]
Решим систему:
\[
\begin{cases}
f(x) = 1 + x f(1 - x), \\
f(1 - x) = 1 + (1 - x) f(x).
\end{cases}
\]
Подставим второе уравнение в первое:
\[
f(x) = 1 + x \left(1 + (1 - x)f(x)\right) \Rightarrow f(x) = 1 + x + x(1 - x)f(x).
\]
Выразим \( f(x) \):
\[
f(x)(1 - x(1 - x)) = 1 + x \Rightarrow f(x) = \frac{x + 1}{x^2 - x + 1}.
\]
Ответ: \( \boxed{f(x) = \dfrac{x + 1}{x^2 - x + 1}} \).
- Найдите параметры \( a \) и \( b \), при которых система не имеет решений:
\[
\begin{cases}
\sin(x + y) = 0, \\
(x - a)^2 + (y - b)^2 < \dfrac{\pi^2}{8}, \\
a^2 + b^2 = \dfrac{9\pi^2}{4}.
\end{cases}
\]
Решение:
Множество \( \sin(x + y) = 0 \) соответствует прямым \( x + y = \pi k \). Условие отсутствия решений требует, чтобы круг \( (x - a)^2 + (y - b)^2 < \left(\dfrac{\pi}{2\sqrt{2}}\right)^2 \) не пересекал эти прямые. Минимальное расстояние от центра круга $(a; b)$ до прямой $ x + y = \pi k $ должно быть \( \geq \dfrac{\pi}{2\sqrt{2}} \). Учитывая \( a^2 + b^2 = \left(\dfrac{3\pi}{2}\right)^2 \), расстояние оценивается:
\[
\dfrac{|a + b - \pi k|}{\sqrt{2}} \geq \dfrac{\pi}{2\sqrt{2}} \Rightarrow |a + b - \pi k| \geq \dfrac{\pi}{2}.
\]
Центр \( (a, b) \) должен находиться вне полосы \( \pi k - \dfrac{\pi}{2} < a + b < \pi k + \dfrac{\pi}{2} \) для всех \( k \). Однако для всех точек на окружности $a^2 + b^2 = \left(\dfrac{3\pi}{2}\right)^2 $ это невозможно, так как радиус окружности достаточно велик для пересечения с указанными полосами. Следовательно, система всегда имеет решения.
Ответ: Нет таких \( a \) и \( b \).
Материалы школы Юайти