ФМШ МИЭМ из 10 в 11 класс 2017 год
Печать
youit.school ©
ФМШ МИЭМ
2017 год
Вариант ФМШ 2017-11-1
- Решите уравнение:
\[
\arcsin x + \arctan x = \frac{\pi}{2}.
\]
- Что называется не вертикальной асимптотой? Может ли для одной функции существовать несколько различных не вертикальных асимптот? Может ли график функции пересекать свою не вертикальную асимптоту? Ответы обоснуйте.
- Постройте график функции:
\[
y = \frac{2\sqrt{x} - |x|}{|x| - 1},
\qquad
y = \frac{\bigl|x^4 - |x|\bigr|^3}{\bigl|x^2 - 2\,|x|\,\sqrt{x}\bigr|}.
\]
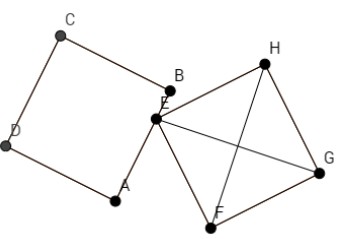
- На плоскости нарисованы два квадрата с одинаковыми длинами сторон, имеющие одну общую точку $E$. Из этой точки начинают движение с постоянными скоростями два точечных объекта: первый движется по сторонам первого квадрата
\[
E \to B \to C \to D \to A \to E \to \dots,
\]
а второй — по сторонам и диагоналям второго квадрата
\[
E \to F \to H \to E \to G \to H \to F \to G \to E \to \dots.
\]
Каким может быть отношение скоростей данных объектов, чтобы через некоторое время они снова одновременно оказались в точке $E$? Смогут ли они когда-либо снова одновременно оказаться в точке $E$, если скорость одного из объектов будет в 2 раза больше скорости другого?
- Решите неравенство:
\[
2^{3^{4^{x}}} \lt 4^{3x}
\]
- Найдите все функции $f(x)$, которые для любых действительных $x$ удовлетворяют условию:
\[
2f(x) + f(1 - x) = x^2.
\]
- При каких значениях параметров $a$ и $b$ система
\[
\begin{cases}
\cos(x - y) = 1, \\
(x - a)^2 + (y - b)^2 < \frac{\pi^2}{2}, \\
a^2 + b^2 = 9\pi^2
\end{cases}
\]
не имеет решений?
Материалы школы Юайти
youit.school ©
Решения задач
- Решите уравнение:
\[
\arcsin x + \arctan x = \frac{\pi}{2}.
\]
Решение:
Обозначим \(\arcsin x = \alpha\), тогда \(x = \sin \alpha\). По условию, \(\arctan x = \frac{\pi}{2} - \alpha\). Возьмем тангенс от обеих частей: \[ x = \tan\left(\frac{\pi}{2} - \alpha\right) = \cot \alpha = \frac{\sqrt{1 - x^2}}{x}. \] Умножая обе стороны на \(x\): \[ x^2 = \sqrt{1 - x^2}. \] Возведем в квадрат: \[ x^4 = 1 - x^2 \quad \Rightarrow \quad x^4 + x^2 - 1 = 0. \] Замена \(z = x^2\): \[ z^2 + z - 1 = 0 \quad \Rightarrow \quad z = \frac{-1 \pm \sqrt{5}}{2}. \] Положительный корень \(z = \frac{\sqrt{5} - 1}{2}\), тогда \(x = \sqrt{\frac{\sqrt{5} - 1}{2}}\).
Ответ: \(\boxed{\sqrt{\dfrac{\sqrt{5} - 1}{2}}}\).
- Что называется не вертикальной асимптотой? Может ли для одной функции существовать несколько различных не вертикальных асимптот? Может ли график функции пересекать свою не вертикальную асимптоту? Ответы обоснуйте.
Решение:
Невертикальная асимптота — это прямая вида \(y = kx + b\) при \(x \to \pm \infty\).
Для функции может существовать до двух различных невертикальных асимптот (при \(x \to +\infty\) и \(x \to -\infty\)). Например, функция \(f(x) = x + \frac{1}{x}\) имеет асимптоты \(y = x\) при \(x \to \pm \infty\).
График функции может пересекать свою невертикальную асимптоту. Например, функция \(f(x) = \frac{\sin x}{x}\) имеет асимптоту \(y = 0\) и бесконечно пересекает ее.
Ответ: Невертикальная асимптота — прямая \(y = kx + b\) при \(x \to \infty\). Да, возможно несколько асимптот. Да, график может пересекать асимптоту.
- Постройте график функции:
\[
y = \frac{2\sqrt{x} - |x|}{|x| - 1},
\qquad
y = \frac{\bigl|x^4 - |x|\bigr|^3}{\bigl|x^2 - 2\,|x|\,\sqrt{x}\bigr|}.
\]
Решение:
Первая функция:
Область определения: \(x \ge 0\), \(x \neq 1\).
Упрощаем для \(x \ge 0\): \[ y = \frac{2\sqrt{x} - x}{x - 1}. \] Исследуем поведение: - При \(x \to 0^+\): \(y \to 0\). - При \(x \to 1^{-}\): \(y \to -\infty\). - При \(x \to 1^{+}\): \(y \to +\infty\). - При \(x \to \infty\): \(y \approx -\frac{x}{x} = -1\).
Вторая функция:
Область определения: \(x \ge 0\), \(x \neq 0, 4\).
Для \(x \ge 0\): \[ y = \frac{|x^4 - x|^3}{|x^2 - 2x\sqrt{x}|} = \frac{|x(x^3 - 1)|^3}{|x||\sqrt{x} - 2|} = x^{3/2}\frac{|x^3 - 1|^3}{|\sqrt{x} - 2|}. \] Исследуем поведение: - При \(x \to 0^+\): \(y \to 0\). - При \(x = 1\): \(y = 0\). - Вертикальная асимптота при \(x = 4\).
- Найдите отношение скоростей двух объектов, движущихся по квадратам, для синхронного возврата в точку \(E\). Возможно ли возвращение при скорости одного в 2 раза больше?
Решение:
Первый объект проходит цикл длиной \(4s\) (стороны квадрата). Второй объект проходит цикл длиной \(8s(1 + \sqrt{2})\) (стороны и диагонали).
Периоды движения: \[ T_1 = \frac{4s}{v_1}, \quad T_2 = \frac{4s(1 + \sqrt{2})}{v_2}. \] Условие синхронизации: \(T_1 = kT_2\), тогда: \[ \frac{v_1}{v_2} = \frac{1 + \sqrt{2}}{k}. \] Отношение скоростей должно быть рациональным кратным \(1 + \sqrt{2}\).
Если \(\frac{v_1}{v_2} = 2\), взаимная иррациональность \(2(1 + \sqrt{2})\) исключает синхронизацию.
Ответ: Отношение \(\frac{v_1}{v_2}\) должно быть рационально \(1 + \sqrt{2}\). При скорости одного вдвое больше, возвращение невозможно.
- Решите неравенство:
\[
2^{3^{4^x}} < 4^{3x}.
\]
Решение:
Преобразуем правую часть: \[ 4^{3x} = 2^{6x}. \] Неравенство принимает вид: \[ 2^{12x} \lt 2^{6x} \Rightarrow x \in (-\infty; 0) \]
Ответ: $x \in (-\infty; 0)$.
- Найдите все функции \(f(x)\), удовлетворяющие условию:
\[
2f(x) + f(1 - x) = x^2.
\]
Решение:
Подставим \(x \to 1 -x\): \[ 2f(1 - x) + f(x) = (1 - x)^2. \] Решаем систему: \[ \begin{cases} 2f(x) + f(1 - x) = x^2, \\ 2f(1 - x) + f(x) = (1 - x)^2. \end{cases} \] Умножим первое уравнение на 2 и вычтем второе: \[ 3f(x) = 2x^2 - (1 -x)^2 \quad \Rightarrow \quad f(x) = \frac{x^2 + 2x -1}{3}. \] Ответ: \(\boxed{f(x) = \dfrac{x^2 + 2x - 1}{3}}\).
- При каких значениях \(a\) и \(b\) система:
\[
\begin{cases}
\cos(x - y) = 1, \\
(x - a)^2 + (y - b)^2 < \frac{\pi^2}{2}, \\
a^2 + b^2 = 9\pi^2
\end{cases}
\]
не имеет решений?
Решение:
Уравнение \(\cos(x - y) = 1\) дает \(x - y = 2\pi n\). Второе неравенство — круг с центром \((a, b)\) радиуса \(\pi/\sqrt{2}\). Окружность из третьего уравнения имеет радиус \(3\pi\).
Система не имеет решений, если расстояние от центра \((a, b)\) до любой прямой \(x - y = 2\pi n\) не менее \(\pi/\sqrt{2}\).
Условие: \(|a - b - 2\pi n| \ge \pi\) для всех \(n \in \mathbb{Z}\), что выполняется при \(|a - b| \ge \pi\) и \(a^2 + b^2 = 9\pi^2\).
Ответ: Система не имеет решений при \(a^2 + b^2 = 9\pi^2\) и \(|a - b| \ge \pi\).
Материалы школы Юайти