ФМЛ №30 из 9 в 10 класс 2020 вариант 1

ЛИЦЕЙ №30 (СПБ)

2020 год

Вариант 1

1. Упростите выражение \[ \bigl(\tfrac{a^{3/2}+b^{3/2}}{a^{1/2}+b^{1/2}}-(a+b)\bigr) \cdot \tfrac{b^{1/2}-a^{1/2}}{a^{1/2}b^{1/2}b^{3/2}-b^{1/2}a^{3/2}} \cdot(\sqrt{a}+\sqrt{b}). \]
2. Найдите сумму всех трёхзначных чисел, которые при делении на 11 дают остаток 5.
3. Банкир в конце года начисляет 20% к сумме, находящейся на счёте в начале года. Каким станет вклад 50 000 рублей через 3 года.
4. При делении двузначного числа на сумму его цифр получили частное 7 и остаток 3, при делении этого же числа на число, записанное теми же цифрами в обратном порядке, получили частное 1 и остаток 36. Найдите это число.
5. Решите уравнение \[ (x^2 + x - 2)\sqrt{x+1} = (x-1)(x^2 + 3x + 2). \]
6. Решить неравенство \[ \frac{x\sqrt{x}+x-5\sqrt{x}+2}{\sqrt{x}-2}\ge x. \]
7. Решите уравнение \[ \bigl(x + \tfrac{1}{x}\bigr)^{2} + 3x = 4 - \tfrac{3}{x}. \]
8. Два велосипедиста выехали одновременно из пункта $A$ в $B$, первый со скоростью 24 км/ч, второй — 18 км/ч. Спустя час вслед за ними выехал автомобиль, который обогнал второго велосипедиста на 10 минут раньше, чем первого. Найдите скорость автомобиля.
9. При каком значении \(a\) сумма корней уравнения \[ 2x^2 - \bigl|a^2 - 3\bigr|\,x = 1 \] больше, чем \(a\)?
10. Построить график функции \[ f(x) = \frac{1 - \lvert x - 2\rvert}{x} \] и решить неравенство \(f(x) \le 2\).
11. Построить график функции \[ f(x) = \lvert x^2 - 6x + 5 \rvert \] и найти, при каком \(k\) этот график имеет три общие точки с графиком функции \[ g(x) = k(x - 7) + 4. \]
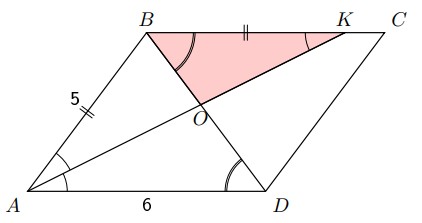
12. $ABCD$ — параллелограмм площадью $22$. $AK$ — биссектриса острого угла $A$, точка $K\in BC$, $AB=5$, $AD=6$, $AK\cap BD=O$. Найти площадь $\triangle BOK$.
    
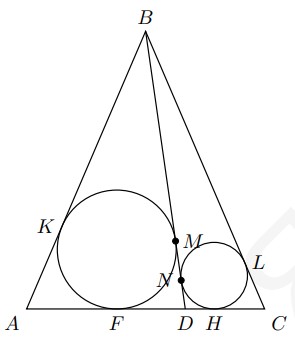
13. $AC$ — основание $p/6\triangle ABC$, $D\in AC$, $AD=4$, $CD=2$. Окружности, вписанные в $\triangle ABD$ и $\triangle DBC$, касаются $BD$ в точках $M$ и $N$ соответственно. Найти длину отрезка $MN$.
    
14. Пусть $\max\{a; b\}$ обозначает большее из чисел $a$ и $b$. Найти наименьшее значение функции \[ m(x) = \max\bigl\{-x^2 + 4x - 2;\,\sqrt{x - 2}\bigr\}. \]

Решения задач

1. Упрощение выражения: \[ \left(\frac{a^{3/2} + b^{3/2}}{a^{1/2} + b^{1/2}} - (a + b)\right) \cdot \frac{b^{1/2} - a^{1/2}}{a^{1/2}b^{5/2} - a^{3/2}b^{1/2}} \cdot (\sqrt{a} + \sqrt{b}). \] Решение: \[ \frac{a^{3/2} + b^{3/2}}{a^{1/2} + b^{1/2}} = a^{1/2} - b^{1/2}; \quad \text{После преобразований получим:} \quad \text{Ответ: } 1. \]
2. Сумма трёхзначных чисел с остатком 5 при делении на 11: \[ \text{Первое число: } 104, \quad \text{последнее: } 995; \quad n = 82; \quad S = \frac{(104 + 995) \cdot 82}{2} = 45059. \]
3. Вклад через 3 года: \[ 50000 \cdot 1.2^3 = 86400 \text{ рублей}. \]
4. Искомое число: 73.
5. Решение уравнения: \[ x = -1, \quad x = 1. \]
6. Решение неравенства: \[ x \in \left[\frac{4}{9}, 1\right] \cup (4, +\infty). \]
7. Решение уравнения: \[ x = -2 \pm \sqrt{3}. \]
8. Скорость автомобиля: 72 км/ч.
9. Значение \( a \): \[ a \in (-\sqrt{3}, 1) \cup (3, +\infty). \]
10. График функции \( f(x) = \frac{1 - \lvert x - 2 \rvert}{x} \). Решение неравенства: \[ x \leq -1 \quad \text{или} \quad 0 < x 2. \]
11. Значение \( k = 1 \).