Физтех-лицей имени П.Л.Капицы из 4 в 5 класс

1. Четыре утенка и пять гусят весят 4 кг 100 г, а пять утят и четыре гусенка весят 4 кг. Сколько весит 1 утенок?
   
   
2. В классе 17 пловцов, 6 борцов и 13 шахматистов. Известно, что каждый спортсмен занимается двумя видами спорта. Сколько в классе спортсменов?
   
   
3. Сколько в зоопарке зверей и сколько птиц, если у них вместе 6000 ног и 2500 голов?
   
   
4. Три яблока, четыре груши и один персик стоят 40~рублей. Одно яблоко, четыре груши и персик стоят 32 рубля. Сколько стоят одно яблоко, одна груша и персик, если персик стоит столько, сколько стоят два яблока?
   
   
5. Сыну 7 лет, а отцу 37. Через сколько лет отец будет втрое старше сына?
   
   
6. Яхта отправилась в плавание в понедельник в полдень. Плавание будет продолжаться 80~часов. Назвать день недели и час её возвращения в порт.
   
   
7. В классе 32 ученика. Из них 18 занимаются в секции лёгкой атлетики, 10 -- в секции плавания и 5 -- в обеих секциях. Сколько учащихся этого класса не занимаются ни в одной из этих секций?
   
   
8. У мальчика столько сестер, сколько и братьев, а у его сестры вдвое меньше сестер, чем братьев. Сколько братьев и сколько сестер в этой семье?
   
   
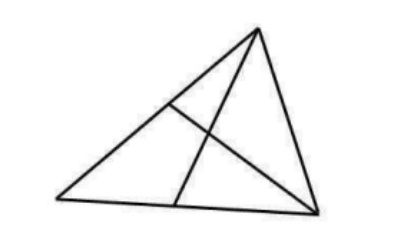
9. Сколько треугольников на рисунке?
   
   
   
   
   
10. Если Сергей купит 15 тетрадей, то у него останется 7 рублей, а на 20 тетрадей у него не хватит 8 рублей. Сколько денег у Сергея?
    
    
11. Развернутый угол разделен на 3 части так, что один из них в два раза меньше второго и в три раза меньше третьего. Найти градусную меру каждого из углов.
    
    
12. На доске написано число 4 839 651 027. Зачеркнуть в нём три цифры так, чтобы оставшиеся цифры в том же порядке образовали наименьшее число.
    
    
13. В стране 19 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в стране?
    
    
14. Расставить 14 стульев вдоль стен в актовом зале, имеющем форму квадрата, так, чтобы у каждой стены стульев стало поровну.
    
    
15. Было 10 листов бумаги. Ученик разрезал некоторые из них на 4 части, после чего стало 28 листов. Сколько листов бумаги разрезал ученик?
    
    
16. Куб со стороной 1 м распилили на кубики со стороной 1 см и выложили в один ряд. Найти длину ряда.
    
    
17. Найти трёхзначное число, которое уменьшается в 10 раз, если зачеркнуть его среднюю цифру.
    
    
18. Класс шел парами. Один из учеников глянул вперед и насчитал 8 пар, затем обернулся назад и насчитал 4 пары. Сколько всего учеников шло в колонне?
    
    
19. Я живу на пятом этаже, а мой брат -- на третьем. Возвращаясь с работы домой, мне приходится пройти 60 ступенек. Сколько ступенек проходит мой брат, когда возвращается домой?
    
    
20. В 10 «А» классе 30 учеников. На родительское собрание пришли 26 мам и 20 пап. У скольких учеников на собрание пришли одновременно и мама, и папа?

Решения задач

1. Четыре утенка и пять гусят весят 4 кг 100 г, а пять утят и четыре гусенка весят 4 кг. Сколько весит 1 утенок?
   Решение: Пусть масса утенка — \( u \), гусенка — \( g \). Составим систему уравнений: \[ \begin{cases} 4u + 5g = 4100 \\ 5u + 4g = 4000 \end{cases} \] Умножим первое уравнение на 5, второе на 4: \[ \begin{cases} 20u + 25g = 20500 \\ 20u + 16g = 16000 \end{cases} \] Вычитая уравнения, получим \( 9g = 4500 \Rightarrow g = 500 \) г. Подставляя \( g \) в первое уравнение: \( 4u + 2500 = 4100 \Rightarrow u = 400 \) г.
   Ответ: 400 г.
   
   
2. В классе 17 пловцов, 6 борцов и 13 шахматистов. Известно, что каждый спортсмен занимается двумя видами спорта. Сколько в классе спортсменов?
   Решение: Сумма всех занятий: \( 17 + 6 + 13 = 36 \). Каждый спортсмен учтен дважды.
   Число спортсменов: \( \frac{36}{2} = 18 \).
   Ответ: 18.
   
   
3. Сколько в зоопарке зверей и сколько птиц, если у них вместе 6000 ног и 2500 голов?
   Решение: Зверей — \( z \), птиц — \( p \): \[ \begin{cases} z + p = 2500 \\ 4z + 2p = 6000 \end{cases} \] Подставляя \( p = 2500 - z \):
   \( 4z + 2(2500 - z) = 6000 \Rightarrow 2z = 1000 \Rightarrow z = 500 \).
   Тогда \( p = 2000 \).
   Ответ: 500 зверей, 2000 птиц.
   
   
4. Три яблока, четыре груши и один персик стоят 40 рублей. Одно яблоко, четыре груши и персик стоят 32 рубля. Сколько стоят одно яблоко, одна груша и персик, если персик стоит столько, сколько стоят два яблока?
   Решение: Пусть цена яблока — \( a \), груши — \( g \), персика — \( p \). Условия: \[ \begin{cases} 3a + 4g + p = 40 \\ a + 4g + p = 32 \\ p = 2a \end{cases} \] Вычтем уравнения: \( 2a = 8 \Rightarrow a = 4 \). Тогда \( p = 8 \). Подставляя в первое уравнение: \( 12 + 4g + 8 = 40 \Rightarrow g = 5 \).
   Ответ: 4 р., 5 р., 8 р.
   
   
5. Сыну 7 лет, а отцу 37. Через сколько лет отец будет втрое старше сына?
   Решение: Через \( x \) лет: \[ 37 + x = 3(7 + x) \Rightarrow x = 8. \] Ответ: 8 лет.
   
   
6. Яхта отправилась в плавание в понедельник в полдень. Плавание будет продолжаться 80 часов. Назвать день недели и час её возвращения в порт.
   Решение: 80 часов = 3 суток 8 часов. Понедельник 12:00 + 3 дня = четверг 12:00 + 8 часов = четверг 20:00.
   Ответ: Четверг, 20:00.
   
   
7. В классе 32 ученика. Из них 18 занимаются в секции лёгкой атлетики, 10 — в секции плавания и 5 — в обеих секциях. Сколько учащихся этого класса не занимаются ни в одной из этих секций?
   Решение: Используем формулу включений-исключений: \( 18 + 10 - 5 = 23 \).
   Не занимаются: \( 32 - 23 = 9 \).
   Ответ: 9.
   
   
8. У мальчика столько сестер, сколько и братьев, а у его сестры вдвое меньше сестер, чем братьев. Сколько братьев и сколько сестер в этой семье?
   Решение: Пусть братьев — \( b \), сестер — \( s \). Для мальчика: \( b = s + 1 \). Для сестры: \( b - 1 = 2(s - 1) \).
   Подставляя \( s = b - 1 \): \( b - 1 = 2(b - 2) \Rightarrow b = 3 \), \( s = 2 \).
   Ответ: 3 брата, 2 сестры.
   
   
9. Сколько треугольников на рисунке?
   Ответ: 13.
   
   
10. Если Сергей купит 15 тетрадей, то у него останется 7 рублей, а на 20 тетрадей у него не хватит 8 рублей. Сколько денег у Сергея?
    Решение: Пусть цена одной тетради — \( x \), деньги — \( d \). Уравнения: \[ \begin{cases} d = 15x + 7 \\ d = 20x - 8 \end{cases} \] Вычитая: \( 5x = 15 \Rightarrow x = 3 \), \( d = 52 \).
    Ответ: 52 рубля.
    
    
11. Развернутый угол разделен на 3 части так, что один из них в два раза меньше второго и в три раза меньше третьего. Найти градусную меру каждого из углов.
    Решение: Пусть меньший угол — \( x \). Тогда \( x + 2x + 3x = 180^\circ \Rightarrow x = 30^\circ \).
    Ответ: \( 30^\circ, 60^\circ, 90^\circ \).
    
    
12. На доске написано число 4839651027. Зачеркнуть в нём три цифры так, чтобы оставшиеся цифры в том же порядке образовали наименьшее число.
    Решение: Минимальное число: 3651027 (зачеркиваем 4,8,9).
    Ответ: 3651027.
    
    
13. В стране 19 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в стране?
    Решение: Число авиалиний: \( \binom{19}{2} = 171 \).
    Ответ: 171.
    
    
14. Расставить 14 стульев вдоль стен в актовом зале, имеющем форму квадрата, так, чтобы у каждой стены стульев стало поровну.
    Ответ: По 3 стула у каждой стены и 2 дополнительных в углах (учитываются для двух стен).
    
    
15. Было 10 листов бумаги. Ученик разрезал некоторые из них на 4 части, после чего стало 28 листов. Сколько листов бумаги разрезал ученик?
    Решение: Каждый разрезанный лист добавляет 3 новых. Разрезано: \( \frac{28 - 10}{3} = 6 \).
    Ответ: 6.
    
    
16. Куб со стороной 1 м распилили на кубики со стороной 1 см и выложили в один ряд. Найти длину ряда.
    Решение: Число кубиков: \( 100 \times 100 \times 100 = 1\,000\,000 \). Длина ряда: \( 1\,000\,000 \) см = 10 км.
    Ответ: 10 км.
    
    
17. Найти трёхзначное число, которое уменьшается в 10 раз, если зачеркнуть его среднюю цифру.
    Решение: Число вида \( 100a + 10b + c \). После удаления средней цифры: \( 10a + c \). Условие: \( \frac{100a + 10b + c}{10} = 10a + c \Rightarrow b = 0 \). Пример: 100.
    Ответ: 100.
    
    
18. Класс шел парами. Один из учеников глянул вперед и насчитал 8 пар, затем обернулся назад и насчитал 4 пары. Сколько всего учеников шло в колонне?
    Решение: Перед ним: \( 8 \times 2 = 16 \). Позади: \( 4 \times 2 = 8 \). Сам ученик: часть пары. Всего учеников: \( 16 + 8 + 2 = 26 \).
    Ответ: 26.
    
    
19. Я живу на пятом этаже, а мой брат — на третьем. Возвращаясь с работы домой, мне приходится пройти 60 ступенек. Сколько ступенек проходит мой брат, когда возвращается домой?
    Решение: Пролётов до 5 этажа: 4. Ступенек на пролёт: \( 60 / 4 = 15 \). Брат проходит 2 пролёта: \( 15 \times 2 = 30 \).
    Ответ: 30.
    
    
20. В 10 «А» классе 30 учеников. На родительское собрание пришли 26 мам и 20 пап. У скольких учеников на собрание пришли одновременно и мама, и папа?
    Решение: Используем формулу включений: \( |A \cap B| = 26 + 20 - 30 = 16 \).
    Ответ: 16.