«Физтех-лицей» им. П. Л. Капицы из 4 в 5 класс 2024 год

Физтех-лицей им. П. Л. Капицы

2024

1. Проверь истинность неравенства: \[ (320 + 85) \cdot (3003 - 93528 \div 36) - 1025 \cdot 160 \ge \frac{2}{5} \cdot \left(390156 \div 78 - \left(638774 - 304 \cdot (617 + 89)\right) \div 85 \right) \]
   
   
2. Реши уравнения:
   1. \(900 - \dfrac{14 \cdot x + 8}{20} = 894\)
   2. \((x + 1 \dfrac{8}{17}) - 9 \dfrac{11}{17} = 3 \dfrac{14}{17}\)
   
   
   
3. Расстояние между теплоходами в 12 часов дня было 455 км. Один теплоход догоняет другой. Скорость первого — 49 км/ч, а второго — \(\dfrac{6}{7}\) от скорости первого. Какое расстояние будет между теплоходами в 15 часов?
   
   
4. Выполни действия:
   1. \(4\text{ м }9\text{ см} + 32\text{ дм }1\text{ см}\)
   2. \(15\text{ м }26\text{ см}^2 - 7\text{ м }245\text{ см}^2\)
   3. \(4\text{ ц }25\text{ кг} \div 5\)
   4. \(20\text{ м }3480\text{ дм}^3 \div 40\)
   
   
   
5. Построй четырёхугольник \(ABCD\), если \(A(1;1)\), \(B(1;4)\), \(C(6;4)\), \(D(6;1)\). Найди его площадь, если 1 клетка = 1 см.

Дополнительные задания

1. Сколько различных букетов из четырёх разных видов цветов можно составить из: роз, астр, лилий, тюльпанов и гладиолусов? (Цветы в букете не упорядочены.)
   
   
2. Три маляра за 5 дней красят 60 окон. Сколько окон покрасят 5 маляров за 4 дня?
   
   
3. Назовём двузначное число «удачным», если оно на 18 больше, чем сумма его цифр. Сколько существует таких «удачных» чисел?
   
   
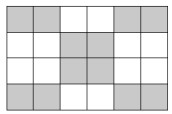
4. Шоколадная плитка состоит из 12 квадратиков тёмного и 12 белого шоколада (в шахматном порядке). Карлсон хочет вырезать по бороздкам квадратик \(2 \times 2\), чтобы в нём тёмного шоколада было не меньше, чем белого. Сколькими способами он может это сделать?
   
   
   
5. У Саши есть три коробки. На первой написано: «Здесь 1 ананас». На второй: «Здесь 2 ананаса». На третьей: «Здесь меньше 7 ананасов». В коробках лежат 10 ананасов, ни одна не пуста, и все надписи ложные. Сколько ананасов в каждой коробке?

Решения задач

1. Проверь истинность неравенства: \[ (320 + 85) \cdot (3003 - 93528 \div 36) - 1025 \cdot 160 \ge \frac{2}{5} \cdot \left(390156 \div 78 - \left(638774 - 304 \cdot (617 + 89)\right) \div 85 \right) \] Решение:
   Левые части:
   $93528 \div 36 = 2598$
   $3003 - 2598 = 405$
   $(320 + 85) = 405$
   $405 \cdot 405 = 164025$
   $1025 \cdot 160 = 164000$
   Левая часть: $164025 - 164000 = 25$
   
   Правые части:
   $617 + 89 = 706$
   $304 \cdot 706 = 214624$
   $638774 - 214624 = 424150$
   $424150 \div 85 = 4990$
   $390156 \div 78 = 5002$
   $5002 - 4990 = 12$
   $\frac{2}{5} \cdot 12 = \frac{24}{5} = 4,8$
   
   Неравенство:
   $25 \ge 4,8$ верно
   Ответ: Неравенство истинно.
   
   
2. Реши уравнения:
   1. \(900 - \dfrac{14 \cdot x + 8}{20} = 894\) Решение:
      $\dfrac{14x + 8}{20} = 900 - 894 = 6$
      $14x + 8 = 6 \cdot 20 = 120$
      $14x = 112 \Rightarrow x = 8$
      Ответ: $8$.
      
      
   2. \((x + 1 \dfrac{8}{17}) - 9 \dfrac{11}{17} = 3 \dfrac{14}{17}\) Решение:
      $x = 3\dfrac{14}{17} + 9\dfrac{11}{17} - 1\dfrac{8}{17}$
      $x = 12\dfrac{25}{17} - 1\dfrac{8}{17} = 11\dfrac{17}{17} = 12$
      Ответ: $12$.
   
   
   
3. Расстояние между теплоходами в 15 часов:
   Скорость второго теплохода: $49 \cdot \dfrac{6}{7} = 42$ км/ч
   Разница скоростей: $49 - 42 = 7$ км/ч
   Время движения до 15:00: 3 часа
   Сближение за 3 часа: $7 \cdot 3 = 21$ км
   Новое расстояние: $455 - 21 = 434$ км
   Ответ: 434 км.
   
   
4. Выполни действия:
   1. $4\text{ м }9\text{ см} + 32\text{ дм }1\text{ см} = 409\text{ см} + 321\text{ см} = 730\text{ см} = 7\text{ м }30\text{ см}$
   2. $15\text{ м }26\text{ см}^2 - 7\text{ м }245\text{ см}^2 = 150026\text{ см}^2 - 70245\text{ см}^2 = 79781\text{ см}^2 = 7\text{ м }9781\text{ см}^2$
   3. $4\text{ ц }25\text{ кг} \div 5 = 425\text{ кг} \div 5 = 85\text{ кг} = 0,85\text{ ц}$
   4. $20\text{ м }3480\text{ дм}^3 \div 40 = 20480\text{ дм}^3 \div 40 = 512\text{ дм}^3$
   
   
   
5. Построй четырёхугольник $ABCD$:
   Координаты точек: прямоугольник со сторонами 5 см и 3 см. Площадь: $5 \cdot 3 = 15$ см$^{2}$
   Ответ: $15$ см$^{2}$.

Дополнительные задания

1. Комбинация цветов: $\binom{5}{4} = 5$ способов
   Ответ: 5 букетов.
   
   
2. Продуктивность маляров:
   Одно окно на маляра в день: $\dfrac{60}{3 \cdot 5} = 4$
   За 4 дня 5 маляров: $4 \cdot 5 \cdot 4 = 80$
   Ответ: 80 окон.
   
   
3. Удачные числа:
   Уравнение: $10a + b = a + b + 18 \Rightarrow 9a = 18 \Rightarrow a = 2$
   Возможные значения $b$ от 0 до 9 ⇒ 10 чисел
   Ответ: 10 чисел.
   
   
4. Квадраты 2×2:
   На стандартной шахматной доске каждый квадрат 2×2 содержит 2 тёмных и 2 белых. Удовлетворяющие варианты: все возможные квадраты. Для плитки 6×4 получим 15 вариантов
   Ответ: 15 способов.
   
   
5. Ложные надписи на коробках:
   Первая коробка ≠1 ⇒ 2,
   Вторая ≠2 ⇒1,
   Третья ≥7 ⇒7. Проверка суммы: $2 + 1 + 7 = 10$
   Ответ: Первая — 2, вторая —1, третья —7.