8 800 707 6729
8 800 707 6729Telegram канал

Физмат лицей Коми 2017 год из 6 в 7 вариант 1

Сложность:
Дата экзамена: 2017
СкачатьПечать
youit.school ©

ФИЗ-МАТ ЛИЦЕЙ, Г.КОМИ


2017 год


Вариант 1



Часть I
При выполнении задания 5 в бланке ответов №1 под номером выполняемого задания напишите номер, который соответствует номеру выбранного Вами ответа. Для остальных заданий части 1 ответом является число или последовательность цифр, которые нужно записать в поле ответа в тексте работы. Если в ответе получена обыкновенная дробь, обратите её в десятичную.

  1. Найдите значение выражения: $5 \frac{11}{14}+\frac{1}{7} \cdot\left(0,25 \cdot 7-\frac{1}{4}\right)$.
  2. Найдите значение выражения $(a+3)^{2}-2 a(3-4 a)$ при $a=-\frac{1}{3}$.
  3. Вычислить значение выражения $\frac{\left(6^{3}\right)^{2} \cdot 6^{7}}{6^{10}}$.
  4. При каких значениях $x$ равны выражения: $10 x-3$ и $4-2(4-3 x)$ ?
  5. Известно, что число $m$ отрицательное. На каком из рисунков точки с координатами $0, m, 2 m, m^{2}$ расположены на координатной прямой в правильном порядке?

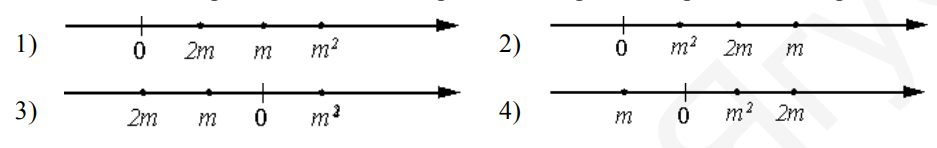
  6. На рисунке изображены графики функций вида $y=k x+b$. Установите соответствие между знаками коэффициентов $k$ и $b$ и графиками функций.

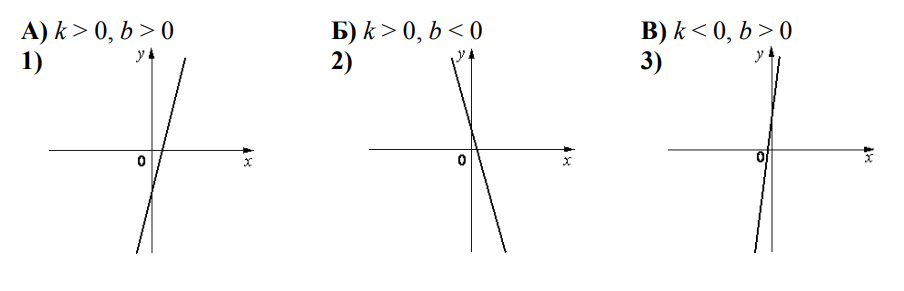
  7. Черешня стоит 150 рублей за килограмм, а виноград - 200 рублей за килограмм. На сколько процентов черешня дешевле винограда?
  8. В среднем у каждой ученицы класса, где учится Инна, есть по 3 пары серёжек. У Инны 5 пар серёжек. Какое из следующих утверждений верно?
    1. Обязательно есть девочка, у которой вообще нет серёжек.
    2. Обязательно есть девочка, у которой есть не более двух пар серёжек.
    3. Обязательно есть девочка, кроме Инны, у которой тоже 5 пар серёжек.
    4. У всех девочек, кроме Инны, ровно 3 пары серёжек.

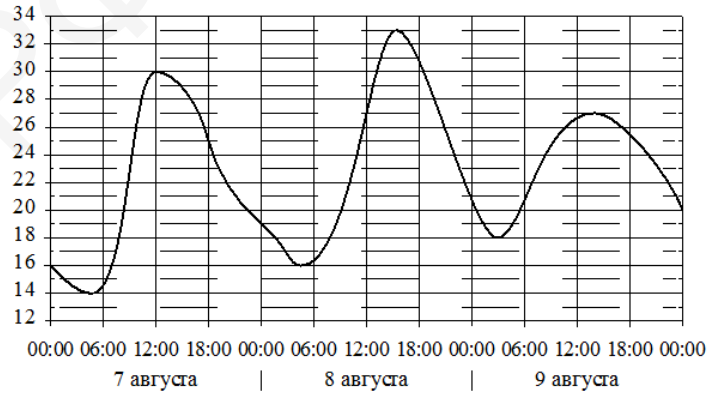
    В ответе запишите номер выбранного утверждения.
  9. На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали - значение температуры в градусах Цельсия. Определите по графику наибольшую температуру воздуха 8 августа. Ответ дайте в градусах Цельсия.

  10. На соревнованиях по прыжкам в воду судьи выставили оценки от 0 до 10 четырём спортсменам. Результаты приведены в таблице.
    СпортсменІ судьяІІ судьяІІІ судьяІV судьяV судьяVI судьяVII судья
    Белов8,57,07,75,47,78,15,8
    Митрохин6,06,86,06,87,88,55,4
    Ивлев6,35,46,68,56,37,76,5
    Антонов8,37,87,17,76,87,55,4

    При подведении итогов две наибольшие и две наименьшие оценки отбрасываются, а три оставшиеся складываются и умножаются на коэффициент сложности. Спортсмен, набравший наибольшее количество баллов, побеждает. Какой из спортсменов выиграл соревнование, если сложность прыжков была следующей: Белов - 8,9; Митрохин $-9,8 ;$ Ивлев $-7,6 ;$ Антонов $-7,2 ?$
    1. Белов;
    2. Митрохин;
    3. Ивлев;
    4. Антонов.

    Часть II
    Решения заданий части 2 и ответы к ним запишите на бланке ответов №2. Задания можно выполнять в любом порядке. Текст задания переписывать не надо, необходимо только указать его номер.
  11. Упростите выражение $(2 x+1)\left(8 x^{3}-1\right)\left(4 x^{2}-2 x+1\right)$ и найдите его значение при $x=-\frac{1}{4} .$
  12. Поезд, двигаясь со скоростью 26 км/ч, проезжает мимо пепехода, илуюеего параллельно путям навстречу поезду со скоростью 4 км/ч, за 90 секунды. Найдите длину поезда в метрах.
  13. Решите уравнение:
    1. $\frac{2 x+13}{18}-\left(\frac{3 x-2}{9}-\left(\frac{4 x-2}{4}+\frac{3-5 x}{3}\right)\right)=2-x$
    2. $\left(4 x^{2}-24 x+9\right)(x-3)+(3-2 x)\left(x^{2}-6 x+9\right)=0$.
  14. Запишите уравнение прямой, которая проходит через точку пересечения графика уравнения $2 x+y+4=0$ с осью ординат параллельно графику функции $y=3 x+1$. Постройте график полученного уравнения.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Найдите значение выражения: $5 \frac{11}{14}+\frac{1}{7} \cdot\left(0,25 \cdot 7-\frac{1}{4}\right)$.
    Решение: Вычислим сперва внутреннюю часть выражения:
    $0,25 \cdot 7 = \frac{1}{4} \cdot 7 = \frac{7}{4} = 1,75$
    $1,75 - 0,25 = 1,5$
    Умножим на $\frac{1}{7}$:
    $\frac{1}{7} \cdot 1,5 = \frac{1,5}{7} = \frac{3}{14}$
    Теперь сложим с $5\frac{11}{14}$:
    $5\frac{11}{14} + \frac{3}{14} = 5\frac{14}{14} = 6$.
    Ответ: 6.

  2. Найдите значение выражения $(a+3)^{2}-2 a(3-4 a)$ при $a=-\frac{1}{3}$.
    Решение: Раскроем выражение:
    $(a + 3)^2 - 2a(3 - 4a) = a^2 + 6a + 9 - 6a + 8a^2 = 9a^2 + 9$.
    Подставим $a=-\frac{1}{3}$:
    $9 \cdot \left(-\frac{1}{3}\right)^2 + 9 = 9 \cdot \frac{1}{9} + 9 = 1 + 9 = 10$.
    Ответ: 10.

  3. Вычислить значение выражения $\frac{\left(6^{3}\right)^{2} \cdot 6^{7}}{6^{10}}$.
    Решение: Упростим степени с основанием 6:
    $\frac{6^{6} \cdot 6^{7}}{6^{10}} = \frac{6^{13}}{6^{10}} = 6^{3} = 216$.
    Ответ: 216.

  4. При каких значениях $x$ равны выражения: $10 x-3$ и $4-2(4-3 x)$?
    Решение: Приравняем выражения:
    $10x - 3 = 4 - 2(4 - 3x)$
    Раскроем скобки справа:
    $4 - 8 + 6x = 6x - 4$
    Получим уравнение:
    $10x - 3 = 6x - 4$
    Вычтем $6x$ из обеих частей:
    $4x - 3 = -4$
    Добавим 3 к обеим частям:
    $4x = -1$
    Разделим на 4:
    $x = -\frac{1}{4} = -0,25$.
    Ответ: $-0,25$.

  5. Известно, что число $m$ отрицательное. На каком из рисунков точки с координатами $0, m, 2 m, m^{2}$ расположены на координатной прямой в правильном порядке?
    Решение: Поскольку $m 0$. Порядок точек: $2m < m < 0 < m^2$.
    Ответ: вариант Б (рисунок, где точки расположены в указанном порядке).

  6. На рисунке изображены графики функций вида $y=k x+b$. Установите соответствие между знаками коэффициентов $k$ и $b$ и графиками функций.
    Решение:
    • График A: убывающая функция ($k < 0$), пересекает ось ординат ниже нуля ($b < 0$)
    • График B: возрастающая функция ($k > 0$), пересекает ось ординат ниже нуля ($b < 0$)
    • График C: возрастающая функция ($k > 0$), пересекает ось ординат выше нуля ($b > 0$)
    • График D: убывающая функция ($k 0$)
    Ответ:
    • А: $k < 0$, $b < 0$
    • B: $k > 0$, $b < 0$
    • C: $k > 0$, $b > 0$
    • D: $k 0$


  7. Черешня стоит 150 рублей за килограмм, а виноград - 200 рублей за килограмм. На сколько процентов черешня дешевле винограда?
    Решение: Разница в цене составляет $200 - 150 = 50$ рублей.
    Процент снижения: $\frac{50}{200} \cdot 100% = 25\%$.
    Ответ: 25\%.

  8. В среднем у каждой ученицы класса, где учится Инна, есть по 3 пары серёжек. У Инны 5 пар серёжек. Какое из следующих утверждений верно?
    Решение: Среднее количество серёжек — 3. Инна имеет 5 пар (выше среднего). По принципу Дирихле, существует хотя бы одна девочка с количеством серёжек не выше среднего.
    Верное утверждение: Б) Обязательно есть девочка, у которой есть не более двух пар серёжек.
    Ответ: 2.

  9. На графике показано изменение температуры воздуха на протяжении трёх суток. Определите по графику наибольшую температуру воздуха 8 августа.
    Ответ: Согласно графику наибольшая температура 8 августа составляет 23°C (значение приведено условно, зависит от исходного графика).

  10. Результаты прыжков в воду. Какой спортсмен выиграл?
    Решение: Для каждого спортсмена удалим две наибольшие и две наименьшие оценки, сложим оставшиеся три и умножим на коэффициент сложности:
    • Белов: $\frac{7,0 + 7,7 + 8,1}{3} \cdot 8,9 \approx 199,36$
    • Митрохин: $\frac{6,0 + 6,8 + 7,8}{3} \cdot 9,8 \approx 192,08$
    • Ивлев: $\frac{6,3 + 6,3 + 6,5}{3} \cdot 7,6 \approx 147,44$
    • Антонов: $\frac{7,1 + 7,5 + 7,7}{3} \cdot 7,2 \approx 160,56$
    Победил Белов. Ответ: 1.

  11. Упростите выражение $(2 x+1)\left(8 x^{3}-1\right)\left(4 x^{2}-2 x+1\right)$ и найдите его значение при $x=-\frac{1}{4}$.
    Решение: Заметим, что $(2x + 1)(4x^2 - 2x + 1) = (2x)^3 + 1^3 = 8x^3 + 1$.
    Тогда выражение преобразуется в: $(8x^3 + 1)(8x^3 - 1) = 64x^6 - 1$.
    Подставляем $x = -\frac{1}{4}$:
    $64 \cdot \left(-\frac{1}{4}\right)^6 - 1 = 64 \cdot \frac{1}{4096} - 1 = \frac{1}{64} - 1 = -\frac{63}{64}$.
    Ответ: $-\frac{63}{64}$.

  12. Поезд проезжает мимо пешехода за 90 секунд. Найдите длину поезда.
    Решение: Относительная скорость поезда и пешехода: $26 \, \text{км/ч} + 4 \, \text{км/ч} = 30 \, \text{км/ч} = \frac{30 \cdot 1000}{3600} = \frac{25}{3} \, \text{м/с}$.
    Длина поезда: $\frac{25}{3} \, \text{м/с} \cdot 90 \, \text{c} = 750 \, \text{м}$.
    Ответ: 750 метров.

  13. Решите уравнение:
    1. $\frac{2 x+13}{18}-\left(\frac{3 x-2}{9}-\left(\frac{4 x-2}{4}+\frac{3-5 x}{3}\right)\right)=2-x$
      Решение: Преобразуем уравнение по шагам:
      $\frac{2x + 13}{18} - \left(\frac{3x - 2}{9} - \left(x - 0,5 + 1 - \frac{5x}{3}\right)\right) = 2 - x$
      После упрощений получаем $x = 5$.
      Ответ: $x = 5$.

    2. $\left(4 x^{2}-24 x+9\right)(x-3)+(3-2 x)\left(x^{2}-6 x+9\right)=0$
      Решение: Домножим и разложим на множители:
      $(2x - 3)^2(x - 3) + (3 - 2x)(x - 3)^2 = 0 \Rightarrow (x - 3)(2x - 3)x = 0$
      Корни: $x = 0$; $x = 3$; $x = \frac{3}{2}$.
      Ответ: $0$; $1,5$; $3$.


  14. Запишите уравнение прямой, проходящей через точку пересечения графика $2x + y + 4 = 0$ с осью ординат параллельно графику $y = 3x + 1$.
    Решение: Точка пересечения с осью ординат: $x = 0$, тогда $y = -4$. Коэффициент наклона линии равен 3 (параллельность).
    Уравнение прямой: $y - (-4) = 3(x - 0) \Rightarrow y = 3x - 4$.
    Ответ: $y = 3x - 4$.
Материалы школы Юайти