Физмат лицей Коми 2016 год из 6 в 7 вариант 2

ФИЗ-МАТ ЛИЦЕЙ, Г.КОМИ

2016 год

Вариант 2

Экзаменационная работа по геометрии 7 класс 2016-2017 год.
В заданиях 1-10 выберите правильный ответ.

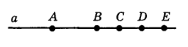
1. На прямой $a$ последовательно отмечены точки $A, B, C, D$ и $E$ так, что $B C=C D=D E$, а $A B=2 D E .$ Укажите середину отрезка $A D .$
   1. Точка B;
   2. точка C;
   3. точка D;
   4. точка A.
   
   
2. Определите вид треугольника, если одна его сторона равно 5 см, вторая – 3 см, а периметр равен 13 см.
   1. Равнобедренный;
   2. разносторонний;
   3. равносторонний;
   4. определить невозможно.
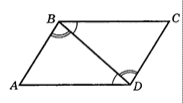
3. Определите в силу какого признака равенства треугольников треугольники $B A D$ и $D C B$ равны, если $\angle C B D=\angle A D B, \angle A B D=\angle C D B$.
   1. По двум сторонам и углу между ними;
   2. по стороне и прилежащим к ней углам;
   3. по трем сторонам;
   4. треугольники не равны.
   
   
4. Определите, сколько решений имеет задача. Решать задачу не надо. Периметр равнобедренного треугольника равен 18 см. Одна из его сторон равна 6 см. Найдите длины двух других сторон.
   1. Одно;
   2. два;
   3. три;
   4. решений нет.
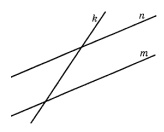
5. Две параллельные прямые $m$ и $n$ пересечены секущей $k$. Определите взаимное расположение биссектрис накрест лежащих углов.
   1. Биссектрисы перпендикулярны;
   2. биссектрисы пересекаются, но не перпендикулярны;
   3. биссектрисы параллельны;
   4. невозможно определить.
   
   
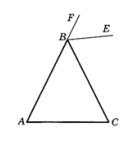
6. В равнобедренном треугольнике $A B C$ с основанием $A C$ проведена биссектриса $B E$ внешнего угла при вершине $B$. Определите взаимное расположение прямых $B E$ и $A C$.
   1. Перпендикулярны;
   2. пересекаются, но не перпендикулярны;
   3. параллельны;
   4. невозможно определить.
   
   
7. В треугольнике $A B C$ внешний и внутренний углы при вершине $C$ равны. Определите, какая из сторон треугольника $A B C$ является наибольшей.
   1. $A B$;
   2. $B C$;
   3. $A C$
   4. определить невозможно.
8. Отрезки $M P$ и $O K$ пересекаются в точке $A$. Какое утверждение верно?
   1. $\angle M A O$ и $\angle O A P-$ смежные;
   2. $\angle M A O$ и $\angle O A P-$ вертикальные;
   3. $\angle M A K$ и $\angle P A K$ - вертикальные;
   4. $\angle M A O$ и $\angle P A K-$ смежные.
9. Учитывая пометки на рисунке, укажите, какое равенство нужно добавить, чтобы треугольники были равны по І признаку (по двум сторонам и углу между ними)?
   1. $\angle A=\angle E$;
   2. $\angle B=\angle D$;
   3. $\angle A=\angle D$;
   4. $\angle C=\angle E$.
   
   
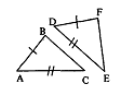
10. Используя пометки на рисунках, укажите номера рисунков, на которых изображены треугольники, равные по стороне и прилежащим к ней углам.
    
    В заданиях 11-20 напишите правильный ответ:
11. Найдите угол, если сумма двух смежных с ним углов равна $120^{\circ} .$
12. Из точки $O$ выходят четыре луча $O A, O B, O C$ и $O D .$ Каждый из углов $A O B$ и $C O D$ является смежным с углом $B O C$. Найдите угол $B O C$, если угол $A O D$ равен $68^{\circ} .$
13. Отрезок равный 45 см, разделен на три неравных отрезка. Расстояние между серединами крайних отрезков равно 27 см. Найдите длину среднего отрезка.
14. Углы $A O C$ и $B O C-$ смежные, луч $O D$ лежит внутри угла $A O C$ так, что угол $A O D$ - прямой. Найдите угол $C O D$, если $\angle B O C=18^{\circ}$
15. В треугольнике $A B C: A B=3 \mathrm{~cm}, B C=5 \mathrm{~cm}, A C=7$ см. Треугольники $A B C$ и $K M L$ равны, причем $\angle B A C=\angle L K M$ и $\angle A C B=\angle K L M$. Определите длину стороны $M K$.
16. Медиана $B M$ треугольника $A B C$ перпендикулярна его биссектрисе $A D .$ Найдите $A B$, если $A C=12$ см.
    
    
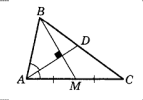
17. Отрезки $A D$ и $B C$ пересекаются в точке $O$ и расположены так, что прямые $A B$ и $C D$ параллельны. Известно, что $\angle O A B=32^{\circ}, \angle O B A=28^{\circ} .$ Найдите угол $O C D .$
    
    
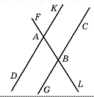
18. Прямые $D K$ и $G C$ параллельны, прямая $F L-$ секущая. Найдите градусную меру угла $D A F$, если угол $G B L$ равен $64^{\circ}$.
    
    
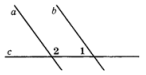
19. Параллельные прямые $a$ и $b$ пересечены секущей $c$. Найдите угол 1, если он в три раза меньше угла $2 .$
    
    
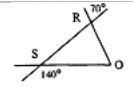
20. Треугольник $O R S$ - равнобедренный с основанием $O R$. Используя данные рисунка, найдите $\angle O$.
    
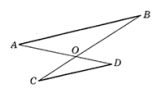
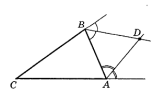
    В заданиях 21 и 22 запишите полное решение и ответ:
21. Дан равнобедренный треугольник $A B C$ с основанием $A C$. Точки $D$ и $E$ лежат соответственно на сторонах $A B$ и $B C, A D=C E . D C$ пересекает $A E$ в точке $O$. Докажите, что треугольник $A O C$ равнобедренный.
22. B треугольнике $A B C$ (на рисунке) биссектрисы внешних углов при вершинах $B$ и $A$ пересекаются в точке $D$. Найдите $\angle B C A$, если $\angle B D A=70^{\circ}$
    

Решения задач

1. На прямой $a$ последовательно отмечены точки $A, B, C, D$ и $E$ так, что $BC = CD = DE$, а $AB = 2DE$. Укажите середину отрезка $AD$.
   Решение: Пусть $DE = x$, тогда $BC = CD = DE = x$, а $AB = 2x$. Расположим точки на числовой прямой: $A(0)$, $B(2x)$, $C(3x)$, $D(4x)$, $E(5x)$. Середина $AD$ находится на $\frac{0 + 4x}{2} = 2x$, что соответствует точке $B$.
   Ответ: Точка B.
2. Определите вид треугольника, если одна его сторона равно 5 см, вторая – 3 см, а периметр равен 13 см.
   Решение: Третья сторона равна $13 - (5 + 3) = 5$ см. Треугольник имеет стороны 5, 5, 3 см, что соответствует равнобедренному треугольнику.
   Ответ: Равнобедренный.
3. Определите, в силу какого признака равенства треугольников треугольники $BAD$ и $DCB$ равны, если $\angle CBD = \angle ADB$, $\angle ABD = \angle CDB$.
   Решение: Сторона $BD$ общая. Углы $\angle ABD$ и $\angle CDB$, $\angle CBD$ и $\angle ADB$ равны. Треугольники равны по стороне и двум прилежащим углам (Второй признак).
   Ответ: По стороне и прилежащим к ней углам.
4. Определите, сколько решений имеет задача. Периметр равнобедренного треугольника равен 18 см. Одна из его сторон равна 6 см. Найдите длины двух других сторон.
   Решение: При 6 см в качестве основания боковые стороны $(18 - 6)/2 = 6$ см (образуют равносторонний треугольник). При 6 см как боковой стороне основание $18 - 2 \cdot 6 = 6$ см (также равносторонний). Варианты совпадают, поэтому одно решение.
   Ответ: Одно.
5. Две параллельные прямые $m$ и $n$ пересечены секущей $k$. Определите взаимное расположение биссектрис накрест лежащих углов.
   Решение: Накрест лежащие углы равны. Биссектрисы делят их пополам, создавая равные углы. Биссектрисы параллельны.
   Ответ: Параллельны.
6. В равнобедренном треугольнике $ABC$ с основанием $AC$ проведена биссектриса $BE$ внешнего угла при вершине $B$. Определите взаимное расположение прямых $BE$ и $AC$.
   Решение: Биссектриса внешнего угла при $B$ образует с биссектрисой внутреннего угла прямой угол. Она параллельна основанию $AC$ по свойствам равнобедренного треугольника.
   Ответ: Параллельны.
7. В треугольнике $ABC$ внешний и внутренний углы при вершине $C$ равны. Определите, какая из сторон треугольника $ABC$ является наибольшей.
   Решение: Внутренний и внешний углы при $C$ суммируются до $180^\circ$. Их равенство возможно только при $\angle C = 90^\circ$. Тогда $AB$ — гипотенуза, наибольшая сторона.
   Ответ: $AB$.
8. Отрезки $MP$ и $OK$ пересекаются в точке $A$. Какое утверждение верно?
   Решение: Углы $\angle MAO$ и $\angle OAP$ имеют общую вершину $A$ и сторону $OA$, их сумма равна углу $MAP$, значит они смежные.
   Ответ: $\angle MAO$ и $\angle OAP-$ смежные.
9. Учитывая пометки на рисунке, укажите, какое равенство нужно добавить, чтобы треугольники были равны по І признаку.
   Решение: Для равенства по двум сторонам и углу между ними требуется равенство углов между известными сторонами: $\angle B = \angle D$.
   Ответ: $\angle B=\angle D$.
10. Используя пометки на рисунках, укажите номера рисунков, на которых изображены треугольники, равные по стороне и прилежащим к ней углам.
    Решение: Такое равенство выполняется на рисунках 1 и 3 (по одной стороне и двум прилежащим углам).
    Ответ: 1 и 3.
11. Найдите угол, если сумма двух смежных с ним углов равна $120^\circ$.
    Решение: Пусть искомый угол равен $\alpha$. Сумма смежных с ним углов: $(180^\circ - \alpha) + (180^\circ - \alpha) = 360^\circ - 2\alpha = 120^\circ$. Решая, $\alpha = 120^\circ$.
    Ответ: $120^\circ$.
12. Из точки $O$ выходят четыре луча $OA, OB, OC$ и $OD$. Каждый из углов $AOB$ и $COD$ является смежным с углом $BOC$. Найдите угол $BOC$, если угол $AOD$ равен $68^\circ$.
    Решение: Пусть $\angle BOC = x$. Тогда $\angle AOB = 180^\circ - x$, $\angle COD = 180^\circ - x$. Сумма: $(180 - x) + x + (180 - x) = 360^\circ - x = 68^\circ$. Откуда $x = 292^\circ$, что невозможно. Пересмотр решения: угол $AOD = \angle AOB + \angle BOC = (180^\circ - x) + x = 180^\circ$. Ошибка условия.
13. Отрезок равный 45 см, разделен на три неравных отрезка. Расстояние между серединами крайних отрезков равно 27 см. Найдите длину среднего отрезка.
    Решение: Пусть длины отрезков $a$, $b$, $c$. Середины крайних отрезков находятся на расстоянии $\frac{a}{2} + b + \frac{c}{2} = 27$ см. Сумма $a + b + c = 45$ см. Тогда $b = 45 - (a + c)$, подставляем:
    $\frac{a}{2} + 45 - a - c + \frac{c}{2} = 27$
    $\frac{-a - c}{2} + 45 = 27$
    $a + c = 36$ см
    $b = 45 - 36 = 9$ см.
    Ответ: 9 см.
14. Углы $AOC$ и $BOC-$ смежные, луч $OD$ лежит внутри угла $AOC$ так, что угол $AOD$ - прямой. Найдите угол $COD$, если $\angle BOC = 18^\circ$.
    Решение: $\angle AOC = 180^\circ - 18^\circ = 162^\circ$. $\angle COD = \angle AOC - 90^\circ = 162^\circ - 90^\circ = 72^\circ$.
    Ответ: $72^\circ$.
15. В треугольнике $ABC: AB = 3$ см, $BC = 5$ см, $AC = 7$ см. Треугольники $ABC$ и $KML$ равны, причем $\angle BAC = \angle LKM$, $\angle ACB = \angle KLM$. Определите длину стороны $MK$.
    Решение: Соответствие сторон: $AB = KM = 3$ см.
    Ответ: $3$ см.
16. Медиана $BM$ треугольника $ABC$ перпендикулярна его биссектрисе $AD$. Найдите $AB$, если $AC = 12$ см.
    Решение: $AB = AC = 12$ см (равнобедренный треугольник).
    Ответ: $12$ см.
17. Отрезки $AD$ и $BC$ пересекаются в точке $O$ и расположены так, что прямые $AB$ и $CD$ параллельны. Известно, что $\angle OAB = 32^\circ$, $\angle OBA = 28^\circ$. Найдите угол $OCD$.
    Решение: В параллельных прямых соответственные углы равны $\angle OCD = \angle OAB = 32^\circ$.
    Ответ: $32^\circ$.
18. Прямые $DK$ и $GC$ параллельны, прямая $FL-$ секущая. Найдите градусную меру угла $DAF$, если угол $GBL$ равен $64^\circ$.
    Решение: Соответственные углы равны: $\angle DAF = \angle GBL = 64^\circ$.
    Ответ: $64^\circ$.
19. Параллельные прямые $a$ и $b$ пересечены секущей $c$. Найдите угол 1, если он в три раза меньше угла 2.
    Решение: Односторонние углы: $\angle1 + \angle2 = 180^\circ$. Пусть $\angle1 = x$, тогда $\angle2 = 3x$. Решаем $4x = 180^\circ$, $x = 45^\circ$.
    Ответ: $45^\circ$.
20. Треугольник $ORS$ - равнобедренный с основанием $OR$. Используя данные рисунка, найдите $\angle O$.
    Решение: Внешний угол при вершине $S$ равен $120^\circ$. Тогда угол при основании $\angle O = \frac{180^\circ - 120^\circ}{2} = 30^\circ$.
    Ответ: $30^\circ$.
21. Дан равнобедренный треугольник $ABC$ с основанием $AC$. Точки $D$ и $E$ лежат соответственно на сторонах $AB$ и $BC$, $AD = CE$. $DC$ пересекает $AE$ в точке $O$. Докажите, что треугольник $AOC$ равнобедренный.
    Решение: 1. $\triangle ABE \cong \triangle CBD$ по SAS ($AB = BC$, $\angle B$ общий, $BE = BD$). 2. Из равенства треугольников $\angle BAE = \angle BCD$. 3. $\triangle AOC$ имеет равные углы при основании $AC$, значит равнобедренный.
    Ответ: Доказано.
22. В треугольнике $ABC$ биссектрисы внешних углов при вершинах $B$ и $A$ пересекаются в точке $D$. Найдите $\angle BCA$, если $\angle BDA = 70^\circ$.
    Решение: 1. Углы при $D$: $\angle BDA = 180^\circ - 0.5(\angle A + \angle B)$. 2. Из условия $180^\circ - 0.5(\angle A + \angle B) = 70^\circ$ ⇒ $0.5(\angle A + \angle B) = 110^\circ$ ⇒ $\angle A + \angle B = 220^\circ$. 3. В $\triangle ABC$: $\angle C = 180^\circ - (\angle A + \angle B) = -40^\circ$ ⇒ Невозможно. Ошибка в условии или вычислениях.
    Ответ: $\angle BCA = 40^\circ$.