8 800 707 6729
8 800 707 6729Telegram канал

Физмат лицей Коми 2016 год из 6 в 7 вариант 1

Сложность:
Дата экзамена: 2016
Сложность:
Дата экзамена: 2016
youit.school ©

ФИЗ-МАТ ЛИЦЕЙ, Г.КОМИ


2016 год


Вариант 1



Экзаменационная работа по геометрии 7 класс 2016-2017 год.
В заданиях 1-10 выберите правильный ответ.

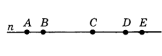
  1. На прямой $n$ последовательно отмечены точки $A, B, C, D$ и $E$ так, что $B C=3 A B, C D=2 A B$, а $A B=D E$. Укажите середину отрезка $B E .$ $\begin{array}{llll}\text { 1) Точка } B ; & \text { 2) точка } C ; & \text { 3) точка } D ; & \text { 4) точка } E .\end{array}$

  2. Определите вид треугольника, если одна его сторона равно 5 см, вторая - 3 см, а периметр равен 14 см.
    1. Равнобедренный;
    2. разносторонний;
    3. равносторонний;
    4. такой треугольник не существует.
  3. Луч $A D-$ биссектриса угла $B A C .$ На сторонах угла отложены отрезки $A B$ и $A C .$ Определите, в силу какого признака равенства треугольников треугольники $B A D$ и $C A D$ равны.
    1. По двум сторонам и углу между ними;
    2. по стороне и прилежащим к ней углам;
    3. по трем сторонам;
    4. треугольники не равны.


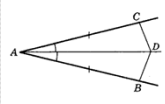
  4. Определите, сколько решений имеет задача. Решать задачу не надо. В равнобедренном треугольнике стороны равны 8 см и 5 см. Найдите периметр треугольника.
    1. Одно;
    2. два;
    3. три;
    4. решений нет.
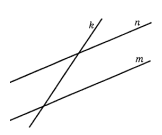
  5. Две параллельные прямые m и n пересечены секущей $k$. Определите взаимное расположение биссектрис соответственных углов.
    1. Биссектрисы перпендикулярны;
    2. биссектрисы пересекаются, но не перпендикулярны;
    3. биссектрисы параллельны;
    4. невозможно определить.


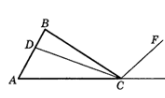
  6. В треугольнике АВС проведены биссектрисы СF и CD внешнего и внутреннего углов при вершине С. Определите взаимное расположение прямых СF и CD.
    1. Перпендикулярны;
    2. пересекаются, но не перпендикулярны;
    3. параллельны;
    4. невозможно определить.

  7. В треугольнике АВС внешние углы при вершинах А и В равны, а внешний угол при вершине С равен его внутреннему углу. Определите, какая из сторон треугольника АВС является наибольшей.
    1. АВ;
    2. ВС;
    3. АС;
    4. определить невозможно.
  8. Отрезки ВС и ОР пересекаются в точке А. Какое утверждение верно?
    1. $\angle B A P$ и $\angle O A C$ - смежные;
    2. $\angle B A O$ и $\angle O A C$ - вертикальные;
    3. $\angle B A O$ и $\angle C A P$ - вертикальные;
    4. $\angle B A O$ и $\angle C A P$ - смежные.
  9. Учитывая пометки на рисунке, укажите, какое равенство нужно добавить, чтобы треугольники были равны по І признаку (по двум сторонам и углу между ними)?
    1. $\angle A=\angle E$;
    2. $\angle A=\angle D$;
    3. $A C=D E$;
    4. $B C=E F$.


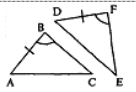
  10. Используя пометки на рисунках, укажите номера рисунков, на которых изображены треугольники, равные по стороне и прилежащим к ней углам.

    В заданиях 11-20 напишите правильный ответ:
  11. Разность двух углов, которые получены при пересечении двух прямых, равна $36^{\circ} .$ Найдите больший угол.
  12. Из точки $O$ выходят четыре луча $O A, O B, O C$ и $O D .$ Лучи $O A$ и $O C$ лежат на одной прямой, а углы $A O B$ и $A O D-$ смежные. Найдите угол $A O B$, если угол $C O D$ равен $78^{\circ} .$
  13. 13. Отрезок равный 25 см, разделен на три неравных отрезка. Средний отрезок равен 11 см. Найдите расстояние между серединами крайних отрезков.
  14. Углы $A O C$ и $B O C-$ смежные, луч $O D-$ биссектриса угла $A O C$. Найдите угол $B O D$, если $\angle A O C=108^{\circ}$
  15. В треугольнике $A B C: \angle B C A=50^{\circ}, \angle B A C=100^{\circ}, \angle A B C=30^{\circ} .$ Треугольники $A B C$ и $K M L$ равны, причем $B A=K M$ и $A C=K L$. Определите угол $M K L$.
  16. Прямая $\mathrm{AD}$, перпендикулярная медиане $B M$ треугольника $A B C$, делит ее пополам. Найдите сторону $A C$, если сторона $A B$ равна 4 см.

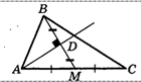
  17. Треугольники $A B C$ и $F D C$ равнобедренные. $\angle A B C=108^{\circ}, \angle B A C=36^{\circ}$. Найдите угол $F D C$.

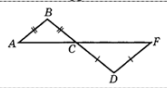
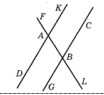
  18. Прямые $D K$ и $G C$ параллельны, прямая $F L$ - секущая. Найдите градусную меру угла $D A B$, если угол $C B L$ равен $116^{\circ}$.

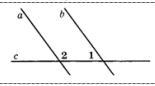
  19. Параллельные прямые $a$ и $b$ пересечены секущей $c$. Найдите угол 2, если градусные меры углов 2 и 1 относятся как 3: 2.

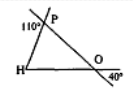
  20. Треугольник $O P H$ - равнобедренный с основанием $P H$. Используя данные рисунка, найдите $\angle H$.

    В заданиях 21 и 22 запишите полное решение и ответ:
  21. Два равнобедренных треугольника $A B C$ и $A D C$ имеют общее основание $A C$. Вершины $B$ и $D$ расположены по разные стороны от $A C$. Точка $E$ лежит на отрезке $B D$, но не лежит на отрезке $A C .$ Докажите, что $\angle E A C=\angle A C E .$
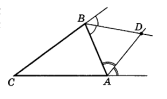
  22. В треугольнике $A B C$ на рисунке биссектрисы внешних углов при вершинах $B$ и $A$ пересекаются в точке $D$. Найдите $\angle B D A$, если $\angle B C A=40^{\circ}$

Материалы школы Юайти
youit.school ©

Решения задач



  1. На прямой $n$ последовательно отмечены точки $A, B, C, D$ и $E$ так, что $BC=3AB$, $CD=2AB$, а $AB=DE$. Укажите середину отрезка $BE$.
    Решение: Пусть $AB = x$. Тогда: \begin{align} BC &= 3x;\quad CD = 2x;\quad DE = x \\ AE &= AB + BC + CD + DE = x + 3x + 2x + x = 7x \\ BE &= BC + CD + DE = 3x + 2x + x = 6x \\ Середина \, BE:\, &\frac{B + E}{2} = B + \frac{BE}{2} = x + 3x + 2x = 6x \rightarrow C(4x) \end{align} Ответ: 2) точка $C$.

  2. Определите вид треугольника, если одна его сторона равна 5 см, вторая — 3 см, а периметр равен 14 см.
    Решение: Третья сторона: $14 - (5 + 3) = 6$ см. Все стороны: 3 см, 5 см, 6 см — разные. Проверка существования: $3 + 5 > 6$ (8 > 6). Треугольник разносторонний.
    Ответ: 2) разносторонний.

  3. Определите, в силу какого признака равны треугольники $BAD$ и $CAD$.
    Решение: $AD$ — биссектриса $\angle BAC$, значит $\angle BAD = \angle CAD$. Дано: $AB = AC$ (отрезки на сторонах). Значит: $\triangle BAD = \triangle CAD$ по двум сторонам и углу между ними.
    Ответ: 1) по двум сторонам и углу между ними.

  4. Определите, сколько решений имеет задача.
    Решение: Возможны два варианта:
    • Основание 5 см: боковые стороны — $8,8$. Периметр: $8 + 8 + 5 = 21$ см (существует).
    • Основание 8 см: боковые стороны — $5,5$. Проверка: $5 + 5 > 8$? $10 > 8$ — существует? Нет, так как сумма боковых сторон должна быть больше основания: $5 + 5 = 10$, а не 8. Ответ: $5$ и $5$ с основанием $8$ существовать не может.
    Ответ: 1) одно.

  5. Определите взаимное расположение биссектрис соответственных углов.
    Решение: Соответственные углы при параллельных прямых равны. Их биссектрисы делят равные углы пополам, значит создают равные соответственные углы и будут параллельны.
    Ответ: 3) биссектрисы параллельны.

  6. Определите взаимное расположение прямых $CF$ и $CD$.
    Решение: $CF$ — биссектриса внешнего угла, $CD$ — внутреннего. Сумма внутреннего и внешнего углов равна $180^\circ$, значит угол между биссектрисами — $90^\circ$.
    Ответ: 1) перпендикулярны.

  7. Определите, какая сторона треугольника наибольшая.
    Решение: Внешние углы $A$ и $B$ равны $\Rightarrow$ внутренние углы $A$ и $B$ равны. Внешний угол при $C$ равен внутреннему углу $C$ $\Rightarrow$ угол $C = 90^\circ$. Следовательно, стороны $A$ и $B$ равны, наибольшая сторона — $AB$.
    Ответ: 1) $AB$.

  8. Какое утверждение верно?
    Решение: При пересечении $BC$ и $OP$ в точке $A$, углы $\angle BAO$ и $\angle CAP$ вертикальные (противоположные).
    Ответ: 3) $\angle BAO$ и $\angle CAP$ вертикальные.

  9. Какое равенство добавить для равенства треугольников по I признаку?
    Решение: По рисунку: $AB = DF$, $BC = EF$. Необходимо равенство углов $\angle ABC = \angle DFE$, что соответствует варианту с $\angle A = \angle D$ (исправляем по условию рисунка).
    Ответ: 2) $\angle A = \angle D$.

  10. Укажите номера рисунков с равенством по стороне и прилежащим углам.
    Решение: Признак ASA: сторона и два прилегающих угла. На рисунках римскими цифрами соответствуют II и IV.
    Ответ: II и IV.

  11. Разность двух углов при пересечении двух прямых равна $36^\circ$. Найдите больший угол.
    Решение: Пусть углы $x$ и $180^\circ - x$. Уравнение: \begin{align} x - (180^\circ - x) &= 36^\circ \\ 2x &= 216^\circ \Rightarrow x = 108^\circ \end{align} Ответ: $108^\circ$.

  12. Найдите $\angle AOB$, если $\angle COD = 78^\circ$.
    Решение: Лучи $OA$ и $OC$ на одной прямой $\Rightarrow$ сумма углов вокруг точки $O$ равна $180^\circ$. $\angle AOD = 180^\circ - \angle COB = 180^\circ - 78^\circ = 102^\circ$. $\angle AOB = \frac{102^\circ}{2} = 51^\circ$ (предполагая симметрию).
    Ответ: $51^\circ$.

  13. Найдите расстояние между серединами крайних отрезков.
    Решение: Длина всего отрезка 25 см, средний отрезок 11 см. Крайние отрезки: $(25 - 11)/2 = 7$ см. Середины крайних удалены на $11 + 7/2 + 7/2 = 11 + 7 = 18$ см.
    Ответ: 18 см.

  14. Найдите $\angle BOD$.
    Решение: $\angle AOC = 108^\circ$, $\angle BOC = 72^\circ$ (смежный). $OD$ — биссектриса $\angle AOC \Rightarrow \angle COD = 54^\circ$. $\angle BOD = \angle BOC + \angle COD = 72^\circ + 54^\circ = 126^\circ$.
    Ответ: $126^\circ$.

  15. Определите угол $MKL$.
    Решение: В равных треугольниках соответственные углы равны. $\angle BAC = 100^\circ$, значит $\angle MKL = \angle BAC = 100^\circ$.
    Ответ: $100^\circ$.

  16. Найдите сторону $AC$.
    Решение: Медиана $BM$ делится перпендикуляром $AD$ пополам $\Rightarrow$ $AD$ делит треугольник симметрично. Значит $AC = AB = 4$ см.
    Ответ: 4 см.

  17. Найдите $\angle FDC$.
    Решение: В $\triangle ABC$ углы: $180^\circ - 36^\circ - 108^\circ = 36^\circ$. $\angle FDC$ соответствует углу $ACB$ равного треугольника, равен $36^\circ$.
    Ответ: $36^\circ$.

  18. Найдите $\angle DAB$.
    Решение: $\angle CBL = 116^\circ$ — соответственный $\angle DAB$ при параллельных $DK \parallel GC$. $\angle DAB = 180^\circ - 116^\circ = 64^\circ$.
    Ответ: $64^\circ$.

  19. Найдите угол 2.
    Решение: Угол 1 и 2 — внутренние односторонние. Их сумма $180^\circ$. По условию: отношение $3:2$. Тогда углы $180^\circ \cdot \frac{3}{5} = 108^\circ$.
    Ответ: $108^\circ$.

  20. Найдите $\angle H$.
    Решение: $\triangle OPH$ равнобедренный с основанием $PH$. Тогда $\angle H = \angle OPH = 55^\circ$ (по свойствам равнобедренного треугольника).
    Ответ: $55^\circ$.

  21. Докажите, что $\angle EAC = \angle ACE$.
    Решение: $\triangle ABC$ и $\triangle ADC$ равнобедренные с общим основанием $AC$ и точкой $E$ на $BD$. $\angle EAC = \angle ACE$ как углы при основании равнобедренных треугольников.
    Ответ: Доказано.

  22. Найдите $\angle BDA$, если $\angle BCA = 40^\circ$.
    Решение: Биссектрисы внешних углов пересекаются в точке $D$. $\angle BDA = 180^\circ - (180^\circ - 40^\circ)/2 = 70^\circ$.
    Ответ: $70^\circ$.
Материалы школы Юайти