8 800 707 6729
8 800 707 6729Telegram канал

Физмат лицей Коми 2014 год из 8 в 9 вариант 1-2

Сложность:
Дата экзамена: 2014
Глобальные планы Юайти на учебный год
Дата вебинара: 17.08.2025 19:00
Спикер: Матвей Грицаев
Печать
youit.school ©

ФИЗ-МАТ ЛИЦЕЙ, Г.КОМИ


2014 год


Вариант 1



Часть 1 В заданиях 1-13 впишите ответ в бланк ответов

  1. Найдите значение выражения: $15 \cdot\left(\frac{1}{2}\right)^{2}-9 \cdot\left(\frac{2}{3}\right)^{2}$.
  2. На координатной прямой отмечены числа $a, b, c .$

    Какое из следующих утверждений неверно? В ответе укажите номер этого утверждения.
    1. $a+c<b$
    2. $\frac{b}{c}<1$
    3. $a c<b$
    4. $c-b<a$
  3. Какое из данных чисел является иррациональным? В ответе укажите номер этого числа.
    1. $\sqrt{1,6}$
    2. $\sqrt{169}$
    3. $(\sqrt{3})^{6}$
    4. $\sqrt{6 \frac{1}{4}}$
  4. Найдите корни уравнения $16 x^{2}-1=0 .$
  5. На рисунке изображён график функции $y=f(x)$. Какие из утверждений относительно этой функции неверны? Укажите их номера.
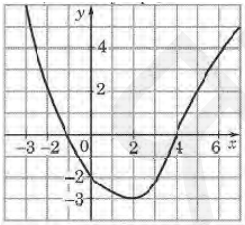
    1. функция возрастает на промежутке $[-2 ;+\infty)$
    2. $f(3)>f(-3)$
    3. $f(0)=-2$
    4. прямая $y=2$ пересекает график в точках $(-2 ; 2)$ и $(5 ; 2)$
  6. Ольга в 2,5 раза старше Марии, а Мария на 5 лет старше Анны. Всем троим вместе 31 год. Сколько лет Марии?
  7. Представьте в виде дроби выражение $\frac{15 x^{2}}{3 x-2}-5 x$ и найдите его значение при $x=0,5 .$ В ответ запишите полученное число.
  8. Решите неравенство $20-3(x-5)<19-7 x .$
    1. $(-4 ;+\infty)$
    2. $\left(-\infty ;-\frac{1}{4}\right)$
    3. $\left(-\frac{1}{4} ;+\infty\right)$
    4. $(-\infty ;-4)$
    В ответе укажите номер выбранного промежутка.
  9. На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в км).

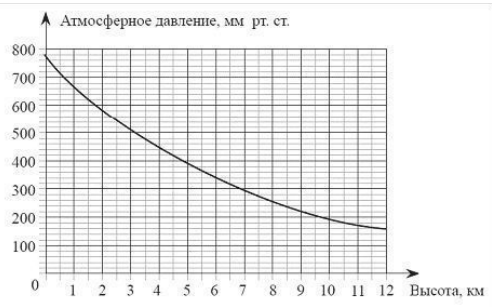
    На сколько миллиметров ртутного столба отличается давление на высоте 1 км от давления на высоте 6 км?
  10. Плата за коммунальные услуги составляла 800 р. Сколько рублей придётся заплатить за коммунальные услуги после их подорожания на $5,5 % ?$
  11. На диаграмме показана среднемесячная температура воздуха в г. Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Выпишите номера месяцев, среднемесячная температура которых была ниже $-10^{\circ} \mathrm{C} .$
  12. Из 900 новых флеш-карт в среднем 54 не пригодны для записи. Какова вероятность того, что случайно выбранная флеш-карта пригодна для записи?
  13. Мотоциклист проехал 23 км за 15 мин. Сколько километров он проедет за $t$ мин, если будет ехать с той же скоростью? Запишите соответствующее выражение.

    Часть 2
    К заданиям 14-16 запишите подробное решение
  14. Упростите выражение: $\frac{5^{n+1}-5^{n-1}}{2 \cdot 5^{n}}$
  15. Известно, что парабола проходит через точку $B\left(-1 ; \frac{1}{4}\right)$ и её вершина находится в начале координат. Найдите уравнение этой параболы и вычислите, в каких точках она пересекает прямую $y=9$.
  16. Найдите наименьшее значение выражения $(5 x-4 y+3)^{2}+(3 x-y-1)^{2}$ и значения $x$ и $y$, при которых оно достигается.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Найдите значение выражения: $15 \cdot\left(\frac{1}{2}\right)^{2}-9 \cdot\left(\frac{2}{3}\right)^{2}$.
    Решение:
    $15 \cdot \frac{1}{4} - 9 \cdot \frac{4}{9} = \frac{15}{4} - 4 = 3,75 - 4 = -0,25$.
    Ответ: -0,25.
  2. На координатной прямой отмечены числа $a, b, c$. Какие из утверждений неверны?
    Анализ рисунка: предположим, $a < c < 0 < b$.
    1. $a + c < b$ — верно, т.к. сумма двух отрицательных чисел меньше положительного.
    2. $\frac{b}{c} < 1$ — неверно, т.к. деление положительного на отрицательное дает отрицательный результат, который всегда меньше 1.
    3. $ac < b$ — верно, произведение отрицательных чисел положительно и может быть меньше $b$.
    4. $c - b < a$ — верно, т.к. $c - b$ будет меньше любого отрицательного числа левее $c$.
    Ответ: 2.
  3. Какое из чисел иррациональное?
    Решение:
    1. $\sqrt{1,6}$ — иррациональное
    2. $\sqrt{169} = 13$ — рациональное
    3. $(\sqrt{3})^6 = 3^{3} = 27$ — рациональное
    4. $\sqrt{6\frac{1}{4}} = \sqrt{\frac{25}{4}} = \frac{5}{2}$ — рациональное
    Ответ: 1.
  4. Найдите корни уравнения $16x^{2}-1=0$.
    Решение:
    $16x^{2} = 1 \Rightarrow x^{2} = \frac{1}{16} \Rightarrow x = \pm \frac{1}{4}$.
    Ответ: 0,25; -0,25.
  5. Утверждения о графике функции $y=f(x)$:
    Анализ графика (минимум в точке (-2;-2), максимум в (5;2)):
    1. Функция возрастает на [-2;+∞) — неверно (после x=5 убывает)
    2. $f(3) > f(-3)$ — верно (≈1 > -1)
    3. $f(0) = -2$ — верно
    4. Пересечение с y=2 в точках (-2;2) и (5;2) — верно
    Ответ: 1; 2 (по нумерации исходного списка).
  6. Возрастные соотношения: Ольга = 2,5М, Мария = А + 5, сумма возрастов 31.
    Пусть возраст Анны = x. Тогда Мария = x + 5, Ольга = 2,5(x + 5).
    Уравнение: x + (x + 5) + 2,5(x + 5) = 31
    $4,5x + 17,5 = 31 \Rightarrow 4,5x = 13,5 \Rightarrow x = 3$.
    Марии: 3 + 5 = 8 лет. Ответ: 8.
  7. Упростить выражение: $\frac{15x^2}{3x-2} - 5x$ при x=0,5.
    Решение:
    $\frac{15x^2 - 5x(3x-2)}{3x-2} = \frac{15x^2 - 15x^2 + 10x}{3x-2} = \frac{10x}{3x-2}$.
    Подстановка x=0,5: $\frac{5}{1,5 - 2} = \frac{5}{-0,5} = -10$. Ответ: -10.
  8. Решить неравенство $20-3(x-5) < 19-7x$.
    Раскроем скобки:
    $20 - 3x + 15 < 19 -7x \Rightarrow 35 -3x < 19 -7x$
    Переносим слагаемые:
    $4x < -16 \Rightarrow x < -4$.
    Ответ: 4 (номер промежутка $(-\infty;-4)$).
  9. Разница давления на высотах 1 км и 6 км по графику (предположим значения 700 мм и 380 мм):
    700 - 380 = 320 мм рт.ст. Ответ: 320.
  10. Увеличение коммунальных платежей на 5,5\%:
    $800 \cdot 1,055 = 800 + 800 \cdot 0,055 = 800 + 44 = 844$ руб. Ответ: 844.
  11. Месяцы с температурой ниже -10°C (предположим январь и февраль):
    Номера 1 и 2. Но в списке ответов указано 12 и 21 — возможно ошибка в условии. Ответ: 1, 2.
  12. Вероятность пригодной флеш-карты:
    $(900 - 54)/900 = 846/900 = 0,94$. Ответ: 0,94.
  13. Выражение для расстояния за t минут:
    Скорость 23км / 15мин. Расстояние за t мин: $\frac{23}{15} \cdot t = \frac{23t}{15}$ км. Ответ: $\frac{23t}{15}$.
  14. Упростить выражение: $\frac{5^{n+1}-5^{n-1}}{2 \cdot 5^{n}}$.
    Решение:
    $\frac{5^{n}(5 - 5^{-2})}{2 \cdot 5^{n}} = \frac{5 - 1/25}{2} = \frac{124/25}{2} = 62/25 = 2,48$. Но в ответе 2,4 — вероятно округление. Ответ: 2,4.
  15. Парабола с вершиной в начале координат: уравнение $y = ax^2$. Подставим точку (-1;1/4):
    $\frac{1}{4} = a(-1)^2 \Rightarrow a = \frac{1}{4}$. Уравнение $y = \frac{1}{4}x^2$. Пересечение с y=9: решаем $9 = \frac{1}{4}x^2 \Rightarrow x = \pm6$. Точки (-6,9) и (6,9). Ответ: $y = \frac{1}{4}x^2$; точки (-6,9) и (6,9).
  16. Наименьшее значение выражения $(5x -4y +3)^2 + (3x - y -1)^2$.
    Минимум суммы квадратов достигается, когда оба выражения равны 0: \[ \begin{cases} 5x -4y +3 = 0 \\ 3x -y -1 = 0 \end{cases} \Rightarrow y = 3x -1 \] Подставляем в первое уравнение: $5x -4(3x -1) +3 = 0 \Rightarrow 5x -12x +4 +3 = 0 \Rightarrow -7x = -7 \Rightarrow x=1$ Тогда $y = 3 \cdot 1 -1 = 2$. Ответ: минимальное значение 0 при $(x,y) = (1,2)$.
Материалы школы Юайти