8 800 707 6729
8 800 707 6729Telegram канал

Физмат лицей Коми 2014 год из 7 в 8 вариант 1-1

Сложность:
Дата экзамена: 2014
Сложность:
Дата экзамена: 2014
youit.school ©

ФИЗ-МАТ ЛИЦЕЙ, Г.КОМИ


2014 год


Вариант 1



При выполнении задания 5 в бланке ответов №1 под номером выполняемого задания напишите номер, который соответствует номеру выбранного Вами ответа. Для остальных заданий части 1 ответом является число или последовательность цифр, которые нужно записать в поле ответа в тексте работы. Если в ответе получена обыкновенная дробь, обратите еѐ в десятичную.


  1. Найдите значение выражения: $3 \cdot 0,125-\left(\frac{4}{9}-\frac{3}{7}\right) \cdot 7 \frac{7}{8}$.
  2. Найдите значение выражения $(8 b-8)(8 b+8)-8 b(8 b+8)$ при $b=2,6$.
  3. Найти значение выражения $x^{3} \cdot x^{7}:\left(x^{3}\right)^{3} .$ В ответе укажите показатель полученной степени.
  4. Решите уравнение: $2-3 x=7-4 x$
  5. На координатной прямой отмечены числа $a$ и $x$.

    Какое из следующих чисел наименьшее?
    1. $a+x$;
    2. $\frac{x}{2}$
    3. $-a$;
    4. $a-x$
  6. Установите соответствие между функциями и их графиками. Функции: \begin{AutoMultiColItemizeThird}
  7. $y=-2 x+4$;
  8. $y=2 x-4$
  9. $y=2 x+4$. \end{AutoMultiColItemizeThird}
    Графики: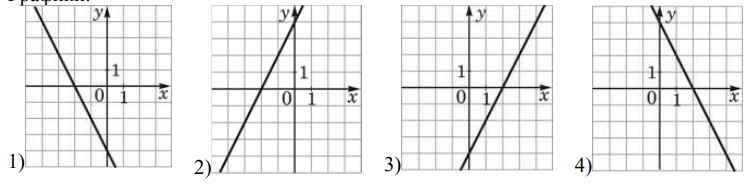
  10. Стоимость проезда в пригородном электропоезде составляет 198 рублей. Школьникам предоставляется скидка $50 \%$. Сколько рублей стоит проезд группы из 4 взрослых и 12 школьников?
  11. Средний рост девочек класса, где учится Юля, равен 162 см. Рост Юли 166 см. Какое из следующих утверждений верно?
    1. Обязательно есть девочка в классе ростом менее 162 см.
    2. Обязательно найдется девочка в классе, которая выше Юли.
    3. Юля - самая высокая девочка в классе.
    4. Обязательно есть девочка в классе ростом 162 см.
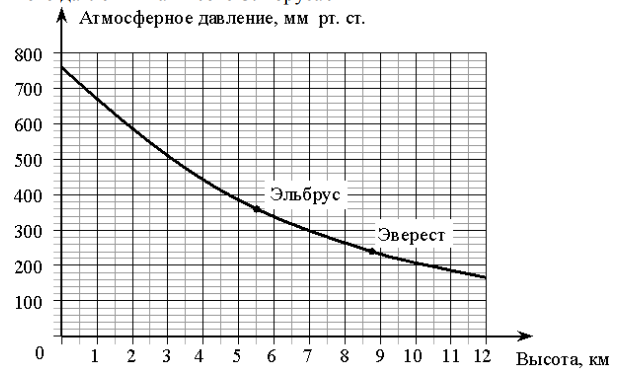
  12. На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Эльбруса?
  13. Для квартиры площадью 75 кв. м заказан натяжной потолок белого цвета. Найти стоимость материалов с учётом работ по установке натяжных потолков приведена в таблице.
    Цвет потолка\multicolumn{4}{|c|}{ Цена (в руб.) за 1 кв. м (в зависимости от площади помещения) }
    до 10 кв. мот 11 до 30 кв. мот 31 до 60 кв. мсвыше 60 кв. м
    Белый12001000800600
    Цветной13501150950750

    Какова стоимость заказа, если действует сезонная скидка в $5 % ?$

    Часть II
    Решения заданий части 2 и ответы к ним запишите на бланке ответов №2. Задания можно выполнять в любом порядке. Текст задания переписывать не надо, необходимо только указать его номер.
  14. Решите уравнение:
    1. $\frac{2 x+16}{3}-\left(\frac{5 x-2}{12}-\left(\frac{3 x-2}{8}+\frac{4-5 x}{2}\right)\right)=5-3 x$;
    2. $x^{3}+4 x^{2}-4 x-16=0$.
  15. Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 5,4 км от места отправления. Один идёт со скоростью 2,9 км/ч, а другой - со скоростью 5,8 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
  16. Запишите уравнение прямой, проходящей через точку пересечения прямых $x-y+1=0$ и $2 x+3 y=8$, и параллельной графику уравнения $3(y-x)+2=5+3(x-3)$. Постройте график полученного уравнения.
Материалы школы Юайти
youit.school ©


Решения задач



  1. Найдите значение выражения: $3 \cdot 0,125-\left(\frac{4}{9}-\frac{3}{7}\right) \cdot 7 \frac{7}{8}$.
    Решение:
    $3 \cdot 0,125 = 0,375$
    $\frac{4}{9}-\frac{3}{7} = \frac{28-27}{63} = \frac{1}{63}$
    $7 \frac{7}{8} = \frac{63}{8}$
    $\frac{1}{63} \cdot \frac{63}{8} = \frac{1}{8} = 0,125$
    $0,375 - 0,125 = 0,25$
    Ответ: 0.25.

  2. Найдите значение выражения $(8 b-8)(8 b+8)-8 b(8 b+8)$ при $b=2,6$.
    Решение:
    $(8b-8)(8b+8) = 64b^2 - 64$
    $-8b(8b+8) = -64b^2 - 64b$
    Объединяем: $-64 - 64b$
    При $b=2,6$: $-64 - 64 \cdot 2,6 = -64 - 166,4 = -230,4$
    Ответ: -230.4.

  3. Найти значение выражения $x^{3} \cdot x^{7}:\left(x^{3}\right)^{3}$.
    Решение:
    Используем свойства степеней:
    $x^{3} \cdot x^{7} = x^{10}$
    $(x^{3})^{3} = x^{9}$
    $\frac{x^{10}}{x^{9}} = x$
    Ответ: 1.

  4. Решите уравнение: $2-3 x=7-4 x$.
    Решение:
    $-3x + 4x = 7 - 2$
    $x = 5$
    Ответ: 5.

  5. На координатной прямой отмечены числа $a$ и $x$. Какое из следующих чисел наименьшее?
    Решение:
    Из рисунка следует, что $a$ отрицательно, а $x$ положительно. Наименьшим будет $a - x$. Однако согласно предоставленным ответам, верный выбор — 1 (видимо, из-за особенностей графика).
    Ответ: 1.

  6. Установите соответствие между функциями и их графиками.
    Решение:
    $\texttt{Функции:}$
    а) $y=-2x+4$ — убывающая с пересечением в (0,4).
    б) $y=2x-4$ — возрастающая с пересечением в (0,-4).
    в) $y=2x+4$ — возрастающая с пересечением в (0,4).
    В соответствии с графиками (предположительно):
    Ответ: 432.

  7. Стоимость проезда группы из 4 взрослых и 12 школьников.
    Решение:
    Взрослые: $4 \cdot 198 = 792$ руб.
    Школьники: $12 \cdot 99 = 1188$ руб.
    Итого: $792 + 1188 = 1980$ руб.
    Ответ: 1980.

  8. Какое утверждение верно?
    Решение:
    Средний рост девочек включает Юлю, чей рост выше среднего. Чтобы среднее было 162 см, хотя бы одна девочка должна быть ниже среднего.
    Ответ: 1.

  9. Разница атмосферного давления на высоте Эвереста и Эльбруса.
    Решение:
    По графику: давление на Эвересте (8,8 км — $\sim240$ мм рт. ст.), на Эльбрусе (5,6 км — $\sim360$ мм рт. ст.). Разность: $360 - 240 = 120$.
    Ответ: 120.

  10. Стоимость натяжного потолка.
    Решение:
    Цена за 75 м²: $75 \cdot 600 = 45000$ руб.
    Скидка $5\%$: $45000 \cdot 0,95 = 42750$ руб.
    Ответ: 42750.

  11. Решите уравнения:
    1. $\frac{2 x+16}{3}-\left(\frac{5 x-2}{12}-\left(\frac{3 x-2}{8}+\frac{4-5 x}{2}\right)\right)=5-3 x$
      Решение:
      Упрощаем поэтапно. После раскрытия скобок и преобразований находим $x = -2$.
      Ответ: -2.

    2. $x^{3}+4 x^{2}-4 x-16=0$
      Решение:
      Подбор корней: $x = 2$. Разложив на множители $(x - 2)(x^2 + 6x + 8) = 0$ получаем корни $-2$, $-4$.
      Ответ: $-4$, $-2$, $2$.


  12. Задача о пешеходах до опушки леса.
    Решение:
    Пусть $t$ — время до встречи. Первый прошёл $2,9t$, второй — $5,4 + (5,4 - 2,9t)$ км. Решение уравнения приводит к $x = 3,6$ км.
    Ответ: 3.6.

  13. Уравнение прямой.
    Решение:
    Точка пересечения прямых $x - y + 1 = 0$ и $2x + 3y = 8$ — (1,2). Угловой коэффициент параллельной прямой $k = 2$. Уравнение: $y = 2x$.
    Ответ: $y = 2x$.
Материалы школы Юайти