8 800 707 6729
8 800 707 6729Telegram канал

Физмат лицей Коми 2014 год из 7 в 8 вариант 1

Сложность:
Дата экзамена: 2014
СкачатьПечать
youit.school ©

ФИЗ-МАТ ЛИЦЕЙ, Г.КОМИ


2014 год


Вариант 1



  1. В заданиях 1-10 выберите правильный ответ.
    Для доказательства равенства треугольников $A P K$ и $D C E$, у которых $A K=E D$ и $\angle A=\angle D$, достаточно доказать, что...
    1. $A P=C D$;
    2. $A P=D E$;
    3. $A P=C E$.
  2. Треугольники $A B C$ и $A_{l} B_{l} C_{l}$ равны, если ...
    1. $A B=A_{1} B_{1}, B C=B_{1} C_{1}, \angle A=\angle A_{1}$;
    2. $A C=A_{l} C_{l} ; B C=B_{l} C_{l} ; \angle C=\angle C_{1}$;
    3. $\angle A=\angle A_{l}, \angle B=\angle B_{l}, \angle C=\angle C_{l}$.
  3. Треугольник равносторонний, если ...
    1. биссектриса треугольника совпадает с его высотой;
    2. медиана треугольника является его высотой и биссектрисой;
    3. любая медиана является высотой.
  4. Биссектрисы $N K$ и $M C$ треугольника $M N F$ пересекаются в точке $O$, тогда $F O$ -
    1. высота;
    2. биссектриса;
    3. медиана.
  5. «Прямые параллельны, если...». Утверждение такого вида называется...
    1. признаком параллельных прямых;
    2. свойством параллельных прямых;
    3. определением параллельных прямых.
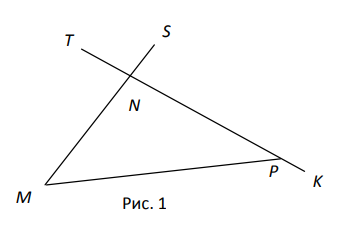
  6. Для данного треугольника (рис. 1) внешним углом является угол...
    1. $\angle S N T$;
    2. $\angle M P T$;
    3. $\angle K P M$.

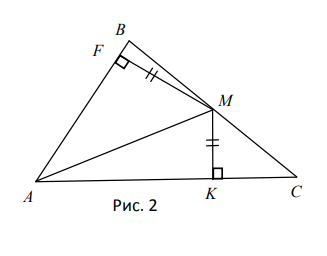
  7. В данном треугольнике (рис. 2) $A M$ является...
    1. биссектрисой;
    2. медианой;
    3. высотой.

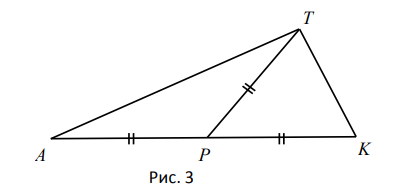
  8. Треугольник $A T K$ (рис. 3 ) $-\ldots$
    1. равнобедренный;
    2. тупоугольный;
    3. прямоугольный.

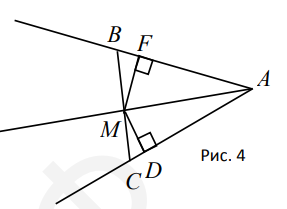
  9. $A M$ - биссектриса $\angle A$ (рис. 4). Из этого не следует, что...
    1. $M B=M C$;
    2. $M F=M D$;
    3. $\angle F M A=\angle D M A$.

  10. В треугольнике $A K P$ сторона $A P=5, A K=10 .$ Сторона $P K$ может быть равна...
    1. 5;
    2. 7;
    3. $17 .$


    В заданиях 11-14 напишите правильный ответ:
  11. В $\triangle A B C \angle A=50^{\circ}$, внешний угол при вершине $\angle B$ равен $94^{\circ} .$ Найти градусную меру $\angle C$.
  12. Разность смежных углов равна $60^{\circ}$. Найти эти углы.
  13. Градусные меры углов треугольника относятся как $2: 3: 5 .$ Найдите градусную меру меньшего из углов треугольника.
  14. На отрезке $B K$ от точки $B$ отложен отрезок $B M$, от точки $K$ - отрезок $K O$, причем $B K=15 \mathrm{~cm}, B M=3 \mathrm{~cm}, K O=7 \mathrm{~cm}$. Найдите длины отрезков $M O$ и $M K .$

    В заданиях 15-17 запишите полное решение и ответ:
  15. Периметр равнобедренного треугольника равен $10 \mathrm{~cm}$, а одна из его сторон равна 4 см. Найдите длины остальных сторон.
  16. В $\triangle A B K \angle A$ составляет $1 / 3$ от $\angle B$ и на $20^{\circ}$ больше $\angle K .$ Найдите углы треугольника.
  17. Внешний угол при вершине $B$ прямоугольного $\triangle A B C$ равен $150^{\circ}$, а биссектриса острого угла $A$ равна 3 см. Найдите длину стороны $B C$.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Для доказательства равенства треугольников $APK$ и $DCE$ по признаку ASA (сторона-угол-сторона) при уже известных $AK=ED$ и $\angle A = \angle D$ требуется равенство сторон $AP=CD$ (расположенных между равными углами). Ответ: (a).
  2. Треугольники равны по признаку SAS (равные стороны $AC=A_1C_1$, $BC=B_1C_1$ и заключенный угол $\angle C = \angle C_1$). Ответ: (b).
  3. В равностороннем треугольнике все медианы являются одновременно высотами и биссектрисами. Ответ: (b).
  4. Точка пересечения биссектрис является центром вписанной окружности, следовательно $FO$ — биссектриса. Ответ: (b).
  5. Утверждение "Прямые параллельны, если..." формулирует признак, а не определение или свойство. Ответ: (a).
  6. Внешний угол смежен со внутренним. Из рисунка видно, что $\angle KPM$ — внешний. Ответ: (c).
  7. На рисунке $AM$ делит угол на два равных, следовательно является биссектрисой. Ответ: (a).
  8. На рисунке угол при вершине $T$ обозначен прямым. Ответ: (c).
  9. Биссектриса делит угол пополам, но не гарантирует равенства сторон $MB=MC$. Ответ: (a).
  10. По неравенству треугольников: $10 - 5 < PK < 10 + 5 \Rightarrow PK=7$. Ответ: (b).
  11. Внешний угол при $B$ равен $94^\circ$, значит внутренний $\angle B = 86^\circ$. Сумма углов: $\angle C = 180^\circ - 50^\circ - 86^\circ = 44^\circ$. Ответ: 44.
  12. Пусть углы $x$ и $180^\circ - x$, их разность: $|x - (180^\circ - x)| = 60^\circ \Rightarrow x=120^\circ$. Углы: $120^\circ$ и $60^\circ$. Ответ: $60^\circ; 120^\circ$.
  13. Сумма частей $2+3+5=10$. Меньший угол: $\frac{180^\circ}{10} \cdot 2 = 36^\circ$. Ответ: 36.
  14. $MO = BK - BM - KO = 15 - 3 - 7 = 5$ см; $MK = BK - BM = 15 -3 =12$ см. Ответ: $5$ см; $12$ см.
  15. Возможные варианты:
    • Если боковые стороны по 4 см: основание $10 - 2\cdot4 =2$ см. Проверка: $4+4>2$ — корректно.
    • Если основание 4 см: боковые стороны $(10-4)/2=3$ см. Проверка: $3+3>4$ — корректно.
    Ответ: $4$ см, $4$ см, $2$ см или $3$ см, $3$ см, $4$ см.
  16. Пусть $\angle A = x$, тогда $\angle B=3x$, $\angle K = x-20^\circ$. Сумма: $x + 3x + (x -20^\circ) =180^\circ \Rightarrow x=40^\circ$. Углы: $40^\circ$, $120^\circ$, $20^\circ$. Ответ: $40^\circ$, $120^\circ$, $20^\circ$.
  17. Внешний угол при $B$ $150^\circ \Rightarrow \angle B=30^\circ$. В прямоугольном треугольнике $\angle A=90^\circ$, $\angle C=60^\circ$. Биссектриса делит $\angle A$ на $45^\circ$. Используя формулу биссектрисы: $l = \frac{2ab\cos(45^\circ)}{a + b} =3 \Rightarrow ab=...$. Из соотношения сторон $BC=AB \cdot tg(60^\circ)= 4.5$ см. Ответ: $4.5$ см.
Материалы школы Юайти