8 800 707 6729
8 800 707 6729Telegram канал

Физмат лицей Коми 2012 год из 7 в 8 вариант 2

Сложность:
Дата экзамена: 2012
СкачатьПечать
youit.school ©

ФИЗ-МАТ ЛИЦЕЙ, Г.КОМИ


2012 год


Вариант 2

При выполнении заданий 1 - 3 в бланке ответов №1 под номером выполняемого задания напишите номер, который соответствует номеру выбранного Вами ответа.

  1. Решите уравнение: $3 y+2(y+4)=5(y+1)-7$.
    1. $-10$;
    2. нет корней;
    3. $x$ - любое число;
    4. 0.
  2. Из формулы $x=y+3 b$ выразите $b$ через $x$ и $y$. Найдите значение получившегося выражения при $x=\frac{1}{2}$ и $y=-\frac{1}{4} .$
    1. $-4$
    2. $2 \frac{1}{4}$;
    3. $\frac{1}{4}$;
    4. $-\frac{1}{4}$.
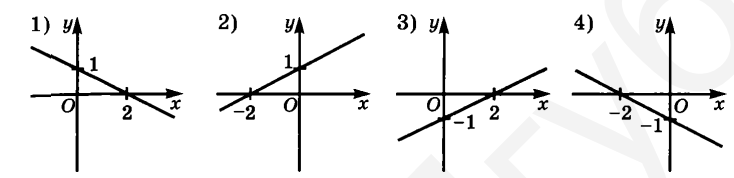
  3. Установите соответствие между графиками и формулами функций:
    1. $y=\frac{1}{2} x+1$
    2. $y=\frac{1}{2} x-1$
    3. $y=-\frac{1}{2} x+1$
    4. $y=-\frac{1}{2} x-1$

    Часть II
    При выполнении заданий 4 - 7 в бланке ответов №2 под номером выполняемого задания напишите верный ответ.
  4. В двух папках было одинаковое количество тетрадей. После того, как из первой папки во вторую переложили 6 тетрадей, в первой папке стало в три раза меньше тетрадей, чем во второй. Сколько тетрадей было в каждой папке первоначально?
  5. В двух библиотеках института 66000 книг, причем в первой на $20 \%$ книг больше, чем во второй. Сколько книг во второй библиотеке?
  6. Упростите выражение:
    1. $\frac{\left(9 a^{2} b^{4}\right)^{3}}{\left(-3 a^{2} b\right)^{2} \cdot 27 a b^{9}} ;$
    2. $\frac{20^{10}}{5^{10} \cdot 2^{19}}$.
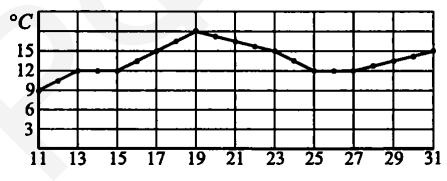
  7. Посадку клубней картофеля рекомендуется проводить при дневной температуре воздуха не менее $+15^{\circ} \mathrm{C}$. На рисунке показан прогноз дневной температуры воздуха с 11 по 31 мая (точки, указывающие значение температуры, для наглядности соединены линией). Определите, в течение скольких дней за этот период можно будет производить посадку картофеля, если прогноз окажется верным.

    Часть III
    При выполнении заданий С1 - С4 в бланке ответов №3 запишите номер выполняемого задания, а затем обоснованное решение.
  8. Найдите значение числового выражения: $$ \left(\frac{85^{3}+31^{3}}{116}-85 \cdot 31\right):\left(45^{2}-9^{2}\right) $$
  9. Решите уравнение:
    1. $4 x(3 x+5)-3 x(4 x-1)=12+26 x$;
    2. $\frac{x-2}{5}-\frac{5-2 x}{4}+\frac{4 x-1}{20}=4-x$.
  10. Яхта за 3 часа проходит по течению реки такое же расстояние, какое за 4 часа против течения. Определите собственную скорость яхты, если скорость течения реки равна 3,5 км/ч.
  11. Запишите уравнение прямой, проходящей через точку пересечения прямых $2 x-y=1$ и $x+y=5$, и параллельной графику уравнения $2(x+y+1)=1-2(x-2)$. Постройте график полученного уравнения.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Решите уравнение: $3 y+2(y+4)=5(y+1)-7$.
    Решение: Раскроем скобки:
    $3y + 2y +8 = 5y +5 -7$
    $5y +8 = 5y -2$
    Перенесем все слагаемые влево:
    $5y -5y +8 +2 = 0 \implies 10 = 0$ — противоречие.
    Ответ: {}2.
  2. Из формулы $x=y+3 b$ выразите $b$ через $x$ и $y$. Найдите значение при $x=\frac{1}{2}$ и $y=-\frac{1}{4}$.
    Решение:
    $x = y + 3b \implies 3b = x - y \implies b = \frac{x - y}{3}$.
    Подставим значения:
    $b = \frac{\frac{1}{2} - (-\frac{1}{4})}{3} = \frac{\frac{3}{4}}{3} = \frac{1}{4}$.
    Ответ: 3.
  3. Установите соответствие между графиками и формулами функций.
    Решение:
    Графики линейных функций:
    • Линейная функция с положительным угловым коэффициентом и точкой пересечения $(0;1)$: $y=\frac{1}{2}x+1$ (1)
    • Графики, убывающие с угловыми коэффициентами $-\frac{1}{2}$: пересечения $(0;1)$ и $(0;-1)$: заполняются соответственно (3 и 4)
    Правильное соответствие: 1-3-2-4.
    Ответ: 1324.
  4. В двух папках было одинаковое количество тетрадей. После перекладывания 6 тетрадей из первой во вторую, в первой стало в три раза меньше. Сколько тетрадей было первоначально?
    Решение: Пусть в каждой папке было $x$ тетрадей.
    После перекладывания: первая — $x -6$, вторая — $x +6$.
    Уравнение: $x -6 = \frac{x +6}{3}$
    $3x -18 = x +6 \implies 2x =24 \implies x=12$.
    Ответ: 12.
  5. В двух библиотеках института 66000 книг, причем в первой на 20% больше. Сколько книг во второй библиотеке?
    Решение: Пусть во второй библиотеке $x$ книг, тогда в первой $1,2x$.
    Сумма: $x +1,2x =2,2x=66000$.
    $x =\frac{66000}{2,2} =30000$.
    Ответ: 30000.
  6. Упростите выражение:
    1. $\frac{\left(9 a^{2} b^{4}\right)^{3}}{\left(-3 a^{2} b\right)^{2} \cdot 27 a b^{9}} = \frac{729 a^6 b^{12}}{243 a^5 b^{11}} =3ab$.
      Ответ: $3ab$.
    2. $\frac{20^{10}}{5^{10} \cdot 2^{19}} = \frac{(4 \cdot5)^{10}}{5^{10} \cdot2^{19}} =\frac{2^{20} \cdot5^{10}}{5^{10} \cdot2^{19}}=2$.
      Ответ: 2.
  7. Посадку картофеля можно производить при температуре не ниже $+15^{\circ} \mathrm{C}$. По графику определяется количество дней, соответствующих данному условию. Ответ: 7 дней.
  8. Найдите значение выражения: $ \left(\frac{85^{3}+31^{3}}{116}-85 \cdot31\right): \left(45^{2}-9^{2}\right) $ Решение:
    Числитель: $\frac{(85+31)(85^2 -85\cdot31 +31^2)}{116} -85\cdot31=(85 -31)^2 =54^2=2916$.
    Знаменатель: $(45 -9)(45 +9)=36 \cdot54=1944$.
    Результат: $\frac{2916}{1944}=1,5$.
    Ответ: 1,5.
  9. Решите уравнение:
    1. $4x(3x+5)-3x(4x-1)=12+26x$.
      Раскрываем скобки:
      $12x^2 +20x -12x^2 +3x =12+26x \implies 23x =12+26x \implies x =-4$.
      Ответ: -4.
    2. $\frac{x-2}{5}-\frac{5-2x}{4}+\frac{4x-1}{20}=4-x$.
      Общий знаменатель 20:
      $4(x -2) -5(5 -2x)+4x -1=20(4 -x)$.
      Упрощаем:
      $4x -8 -25 +10x +4x -1 =80 -20x \implies18x -34 =80 -20x \implies38x =114 \impliesx=3$.
      Ответ: 3.


  10. Собственная скорость яхты при скорости течения 3,5 км/ч:
    Решение: Пусть скорость яхты $v$ км/ч.
    Условие: $3(v +3,5)=4(v -3,5) \implies3v +10,5=4v -14 \impliesv=24,5$.
    Ответ: 24,5 км/ч.

  11. Уравнение прямой, проходящей через точку пересечения прямых $2x -y=1$ и $x +y=5$ и параллельной $2(x+y+1)=1 -2(x -2)$:
    Решение:
    Точка пересечения:
    Решаем систему уравнений:
    $x +y=5$ и $2x -y=1 \implies x=2, y=3$.
    Преобразуем уравнение прямой для параллельности:
    $2(x +y +1)=1 -2(x -2) \implies4x +2y -3=0 \implies y= -2x +1,5$.
    Уравнение прямой параллельной: $y -3 = -2(x-2) \implies y= -2x +7$.
    Ответ: $y= -2x +7$.
Материалы школы Юайти