Физмат лицей Коми 2012 год из 7 в 8 вариант 1

ФИЗ-МАТ ЛИЦЕЙ, Г.КОМИ

2012 год

Вариант 1

При выполнении заданий А1 – А3 в бланке ответов №1 под номером выполняемого задания напишите номер, который соответствует номеру выбранного Вами ответа.

1. Решите уравнение: $6(x-1)-4 x=2(x+2)$.
   1. 0;
   2. x-любое число;
   3. 10;
   4. нет корней.
2. Из формулы $x=y-3 b$ выразите $b$ через $x$ и $y$. Найдите значение получившегося выражения при $x=\frac{1}{2}$ и $y=-\frac{1}{4}$.
   1. $-4$
   2. $-2 \frac{1}{4}$
   3. $\frac{1}{4}$
   4. $-\frac{1}{4}$.
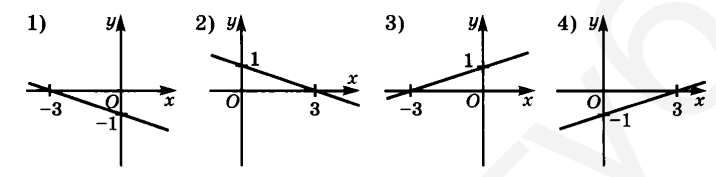
3. Установите соответствие между графиками и формулами функций:
   1. $y=-\frac{1}{3} x+1$
   2. $y=\frac{1}{3} x-1$
   3. $y=-\frac{1}{3} x-1$
   4. $y=\frac{1}{3} x+1$
   
   
   Часть II
   При выполнении заданий 4 - 7 в бланке ответов №2 под номером выполняемого задания напишите верный ответ.
4. В двух бригадах было одинаковое количество рабочих. После того как из первой бригады перевели во вторую 8 рабочих, в ней стало в три раза меньше рабочих, чем во второй бригаде. Сколько рабочих было в каждой бригаде первоначально?
5. В магазин привезли 76 ящиков с персиками и абрикосами, причем ящиков с абрикосами на $10 \%$ меньше, чем с персиками. Сколько привезли ящиков с персиками?
6. Упростите выражение:
   1. $\frac{\left(-2 c y^{3}\right)^{2} \cdot 8 c^{5} y}{\left(4 c^{3} y^{3}\right)^{2}}$
   2. $\frac{12^{9}}{3^{8} \cdot 8^{6}}$
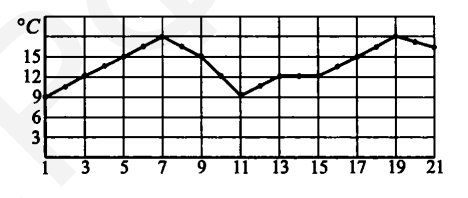
7. Посев семян моркови рекомендуется проводить при дневной температуре воздуха не менее $+12^{\circ} \mathrm{C}$. На рисунке показан прогноз дневной температуры воздуха в первые три недели мая (точки, указывающие значение температуры, для наглядности соединены линией). Определите, в течение скольких дней за этот период можно будет производить посев семян моркови, если прогноз окажется верным.
   
   Часть III
   При выполнении заданий 9 - 12 в бланке ответов №3 запишите номер выполняемого задания, а затем обоснованное решение.
8. Найдите значение числового выражения: $$ \left(\frac{97^{3}+83^{3}}{180}-97 \cdot 83\right):\left(35^{2}-28^{2}\right) $$
9. Решите уравнение:
   1. $(9 x-1)(x+3)-(3 x-1)(3 x+2)=22$;
   2. $\frac{2 x+3}{2}=\frac{x+2}{3}-\frac{1-x}{4}$.
10. Теплоход проходит за 6 часов по течению реки столько же, сколько за 8 часов против течения. Найдите скорость течения реки, если собственная скорость теплохода равна 14 км/ч.
11. Запишите уравнение прямой, проходящей через точку пересечения прямых $2 x+y=3$ и $2 y-x=1$, и параллельной графику уравнения $2(x-y+3)=1-2(x+6)$. Постройте график полученного уравнения.

Решения задач

1. Решите уравнение: $6(x-1)-4 x=2(x+2)$.
   Решение:
   $6x - 6 - 4x = 2x + 4 \implies 2x - 6 = 2x + 4 \implies -6 = 4$ \quad \text{(неверное равенство)}
   Ответ: нет корней.
2. Из формулы $x=y-3 b$ выразите $b$ через $x$ и $y$. Найдите значение получившегося выражения при $x=\frac{1}{2}$ и $y=-\frac{1}{4}$.
   Решение:
   $x = y - 3b \implies 3b = y - x \implies b = \frac{y - x}{3}$
   Подставляем значения:
   $b = \frac{-\frac{1}{4} - \frac{1}{2}}{3} = \frac{-\frac{3}{4}}{3} = -\frac{1}{4}$
   Ответ: $-\frac{1}{4}$.
3. Установите соответствие между графиками и формулами функций:
   Ответ: 2413 (на основе положения прямых и угловых коэффициентов).
   
   
4. В двух бригадах было одинаковое количество рабочих. После того как из первой бригады перевели во вторую 8 рабочих, в первой стало в три раза меньше рабочих, чем во второй бригаде. Сколько рабочих было в каждой бригаде первоначально?
   Решение:
   Пусть в каждой бригаде было x рабочих. После перевода стало:
   Первая бригада: $\quad x - 8$
   Вторая бригада: $\quad x + 8$
   Условие: $x + 8 = 3(x - 8)$
   Решение:
   $x + 8 = 3x - 24 \implies 2x = 32 \implies x = 16$
   Ответ: 16.
5. В магазин привезли 76 ящиков с персиками и абрикосами, причем ящиков с абрикосами на $10 \%$ меньше, чем с персиками. Сколько привезли ящиков с персиками?
   Решение:
   Пусть ящиков с персиками: x
   С абрикосами: $\quad 0,9x$
   Всего: $x + 0,9x = 1,9x = 76 \implies x = \frac{76}{1,9} = 40$
   Ответ: 40.
6. Упростите выражение:
   а) $\frac{\left(-2 c y^{3}\right)^{2} \cdot 8 c^{5} y}{\left(4 c^{3} y^{3}\right)^{2}}$
   Решение:
   $\frac{4c^{2}y^{6} \cdot 8c^{5}y}{16c^{6}y^{6}} = \frac{32c^{7}y^{7}}{16c^{6}y^{6}} = 2cy$
   
   б) $\frac{12^{9}}{3^{8} \cdot 8^{6}}$
   Решение:
   $\frac{(3 \cdot 4)^{9}}{3^{8} \cdot (2^{3})^{6}} = \frac{3^{9} \cdot 2^{18}}{3^{8} \cdot 2^{18}} = 3$
   Ответ: а) $2cy$; б) $3$.
7. Определите количество дней в трёх неделях мая с температурой $\geq +12^{\circ} \mathrm{C}$
   Ответ: 19 дней (на основе подсчёта дней выше заданной температуры по графику).
8. Найдите значение числового выражения: $ \left(\frac{97^{3}+83^{3}}{180}-97 \cdot 83\right):\left(35^{2}-28^{2}\right) $ Решение:
   В числителе:
   $\frac{(97 + 83)(97^{2} - 97 \cdot 83 + 83^{2})}{180} - 97 \cdot 83 = 97^{2} - 2 \cdot 97 \cdot 83 + 83^{2} = (97 - 83)^2 = 196$
   В знаменателе:
   $35^2 - 28^2 = (35 - 28)(35 + 28) = 7 \cdot 63 = 441$
   Итог: $\frac{196}{441} = \frac{4}{9}$
   Ответ: $\frac{4}{9}$.
9. Решите уравнение:
   а) $(9x-1)(x+3)-(3x-1)(3x+2)=22$
   Решение:
   Раскрываем скобки:
   $9x^2 + 27x - x - 3 - (9x^2 + 6x - 3x - 2) = 22$
   Упрощаем: $23x - 1 = 22 \implies x = 1$
   б) $\frac{2x+3}{2} = \frac{x+2}{3} - \frac{1-x}{4}$
   Решение:
   Умножаем на 12: $6(2x + 3) = 4(x + 2) - 3(1 - x)$
   Получаем: $12x + 18 = 7x + 5 \implies x = -\frac{13}{5} = -2,6$
   Ответ: а) 1; б) $-2,6$.
10. Теплоход проходит за 6 часов по течению реки столько же, сколько за 8 часов против течения. Найдите скорость течения реки, если собственная скорость теплохода равна 14 км/ч.
    Решение:
    Пусть скорость течения: v км/ч
    Уравнение расстояний: $(14 + v) \cdot 6 = (14 - v) \cdot 8$
    Решение: $84 + 6v = 112 - 8v \implies 14v = 28 \implies v = 2$
    Ответ: 2 км/ч.
11. Запишите уравнение прямой, проходящей через точку пересечения прямых $2x+y=3$ и $2y-x=1$, и параллельной графику уравнения $2(x-y+3)=1-2(x+6)$.
    Решение:
    Точка пересечения:
    Решим систему:
    $\begin{cases} 2x + y = 3 \\ -x + 2y = 1 \end{cases} \implies x = 2y - 1$
    Подставляем в первое уравнение: $2(2y - 1) + y = 3 \implies y = 1$, тогда $x = 1$
    Направляющий коэффициент параллельной прямой из уравнения:
    $2(x - y + 3) = 1 - 2(x + 6) \implies y = 2x + 9 \implies k = 2$
    Искомое уравнение: $y = 2x + b$, подставляем точку (1,1): $1 = 2 \cdot 1 + b \implies b = -1$
    Уравнение: $y = 2x - 1$
    Ответ: $y = 2x - 1$.